3.6 直线和圆的位置关系(第2课时) 切线的判定与三角形的内切圆 课件(共33张PPT)
文档属性
| 名称 | 3.6 直线和圆的位置关系(第2课时) 切线的判定与三角形的内切圆 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 21:25:12 | ||
图片预览





文档简介
数学北师大版
九年级
第三章 圆
3.6 直线和圆的位置关系
第2课时 切线的判定与三角形的内切圆
B
●O
A
┓
d
α
┏
d
α
d
┓
l
(1)圆心O到直线l的距离d
从等于半径开始,慢慢变短直到0,
然后又开始变长直到等于半径。
直线l与☉O的位置关系从相切到相交,最后到相切。
如图,AB是☉0的直径,直线l经过点A,AB与AC的夹角为∠α
(1)观察直线l转动,点O到l的距离d如何变化?直线l与☉O的位置关系如何变化?
(2)当∠α等于多少度时,点0到l的距离d等于半径r?此时,直线l与☉0有怎样的位置关系?为什么?
C
D
(2)当∠a=90?
相切
α
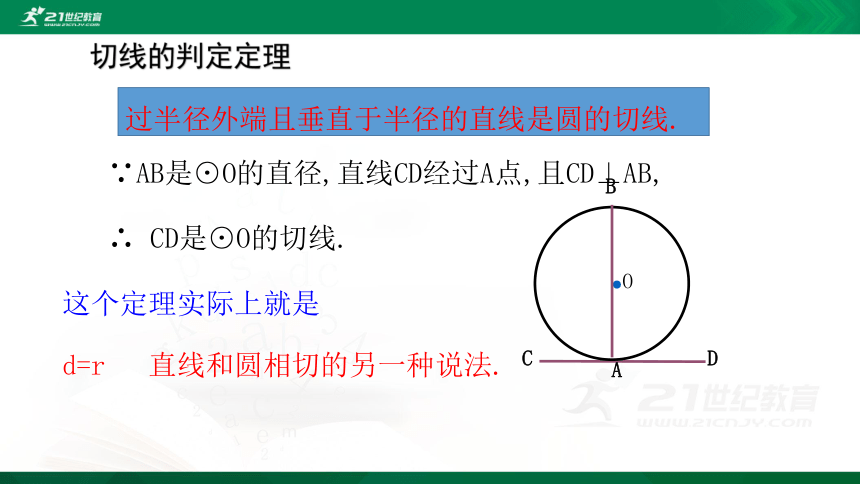
过半径外端且垂直于半径的直线是圆的切线.
C
D
B
●O
A
∵AB是⊙O的直径,直线CD经过A点,且CD⊥AB,
∴ CD是⊙O的切线.
这个定理实际上就是
d=r 直线和圆相切的另一种说法.
切线的判定定理
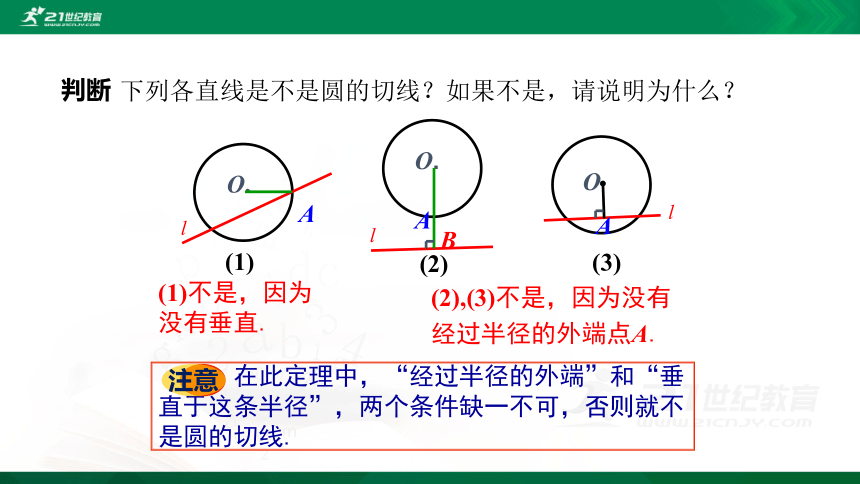
下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
注意
判断
例1 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O的切线.
O
B
A
C
证明:连接OC.
∵ OA=OB,CA=CB,
∴ OC是等腰△OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径,
∴ AB是⊙O的切线.
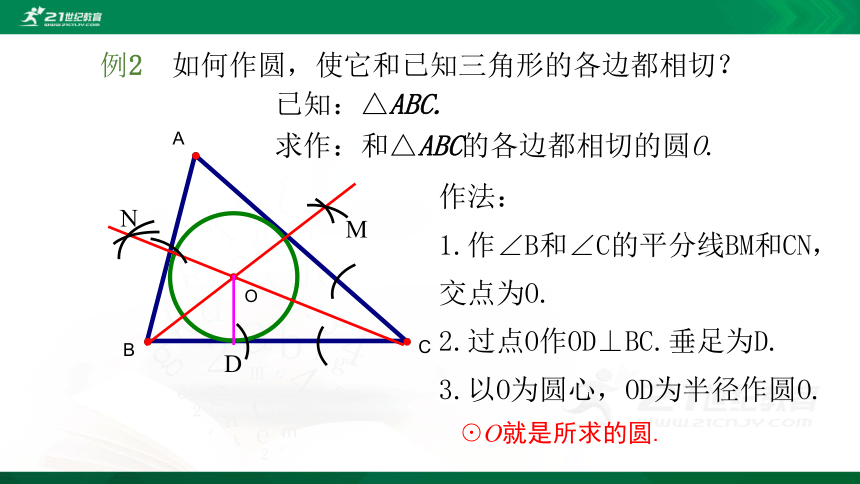
作法:
1.作∠B和∠C的平分线BM和CN,交点为O.
2.过点O作OD⊥BC.垂足为D.
3.以O为圆心,OD为半径作圆O.
☉O就是所求的圆.
M
N
D
例2 如何作圆,使它和已知三角形的各边都相切?
已知:△ABC.
求作:和△ABC的各边都相切的圆O.
由作图过程可知,BE和CF只有一个交点O,并且O到△ABC三边的距离相等、因此和三角形二边都相切的圆可以作出一个,并且只能作出一个,这个圆叫做三角形的内切圆
D
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
3.三角形的内心到三角形的三边的距离相等.
4.三角形的内心就是三角形的三条角平分线的交点.
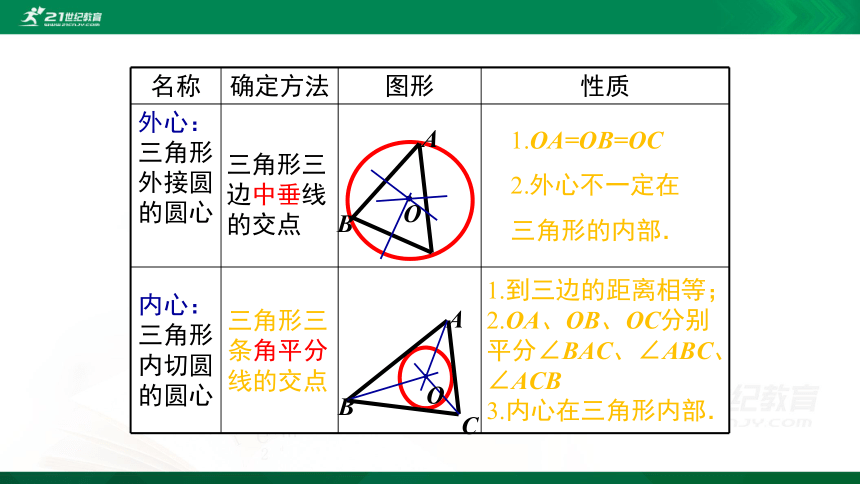
名称
确定方法
图形
性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边中垂线的交点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条角平分线的交点
1.到三边的距离相等;
2.OA、OB、OC分别
平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
A
B
O
A
B
C
O
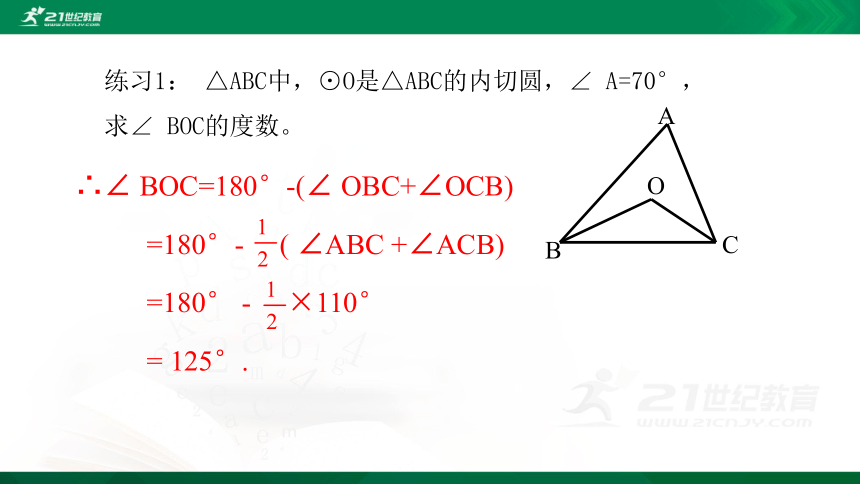
练习1: △ABC中,⊙O是△ABC的内切圆,∠ A=70°,
求∠ BOC的度数。
A
B
C
O
∴∠ BOC=180°-(∠ OBC+∠OCB)
=180°- ( ∠ABC +∠ACB)
=180° - ×110°
= 125°.
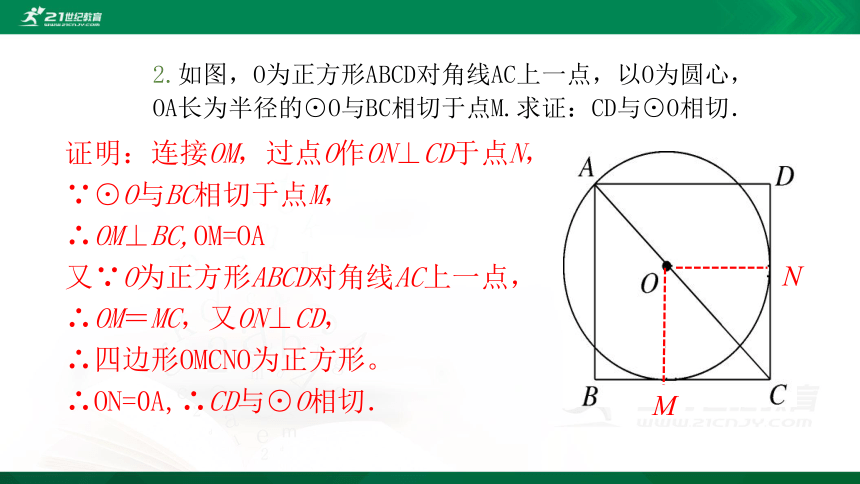
2.如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.
证明:连接OM,过点O作ON⊥CD于点N,
∵⊙O与BC相切于点M,
∴OM⊥BC,OM=OA
又∵O为正方形ABCD对角线AC上一点,
∴OM=MC,又ON⊥CD,
∴四边形OMCNO为正方形。
∴ON=0A,∴CD与⊙O相切.
M
N
课后作业
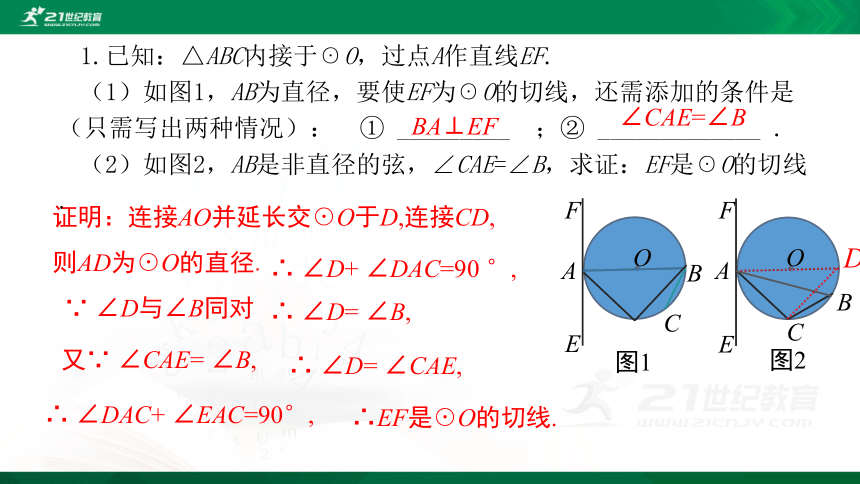
1.已知:△ABC内接于☉O,过点A作直线EF.
(1)如图1,AB为直径,要使EF为☉O的切线,还需添加的条件是(只需写出两种情况): ① _________ ;② _____________ .
(2)如图2,AB是非直径的弦,∠CAE=∠B,求证:EF是☉O的切线.
BA⊥EF
∠CAE=∠B
A
F
E
O
A
F
E
O
B
C
B
C
图1
图2
证明:连接AO并延长交☉O于D,连接CD,则AD为☉O的直径.
∴ ∠D+ ∠DAC=90 °,
∴EF是☉O的切线.
∴ ∠DAC+ ∠EAC=90°,
∴ ∠D= ∠CAE,
又∵ ∠CAE= ∠B,
∴ ∠D= ∠B,
∵ ∠D与∠B同对
D
2.如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=AB·AE,求证:DE是⊙O的切线.
∵AD2=AB·AE,∠BAD=∠DAE,
∴△BAD∽△DAE,∴∠ADB=∠E.
又∵∠ADB=∠ACB,∴∠ACB=∠E,BC∥DE,
∴∠CDE=∠BCD=∠BAD=∠DAC,
又∵∠CAF=∠CDF,
∴∠FDE=∠CDE+∠CDF=∠DAC+∠CAF=∠DAF=90°,
故DE是⊙O的切线.
证明:连接DC,DO,并延长DO交⊙O于F,连接AF.
F
3.如图,已知E是△ABC的内心,∠A的平分线交BC于点F,且与△ABC的外接圆相交于点D.
(1)证明:∵E是△ABC的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
又∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
∴∠CBE+∠CBD=∠ABE+∠BAD.
即∠DBE=∠DEB,
故BD=ED;
(1)求证:BD=ED;
(2)若AD=8cm,DF∶FA=1∶3.求DE的长.
(2)解:∵AD=8cm,DF∶FA=1∶3,
∴DF= AD= ×8=2(cm).
∵∠CBD=∠BAD,∠D=∠D,∴△BDF∽△ADB,∴ ,
∴BD2=AD·DF=8×2=16,
∴BD=4cm,
又∵BD=DE,
3.如图,已知E是△ABC的内心,∠A的平分线交BC于点F,且与△ABC的外接圆相交于点D.
∴DE=4cm.
4.如图,以△ABC的BC边上一点0为圆心的圆,经过AB两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于点F,AC=FC(1)求证:AC是☉0的切线;(2)已知圆的半径R=5,EF=3,求DF的长.
(2)解:在Rt△OFD中,OF =5-3=2,0D =5,
(1)证明:连接OD,OA ,
∵D是BE的中点,BE是直径,
∴OD⊥BE,
∵∠ODF+∠OFD=90°,
∴0A=0D,
∴ ∠OAD =∠ODA,
∵AC=FC,
∴∠CAF=∠CFA=∠OFD.
∴∠0AC=90°
∴AC是☉0的切线;
5.(德化·中考)如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论.
(2)若tan∠ACB= ,BC=2,
求⊙O的半径.
E
A
B
C
D
F
O
解:(1)直线CE与⊙O相切.
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC ,
又 ∵∠ACB=∠DCE,
∴∠DAC=∠DCE,连接OE,则∠DAC=∠AEO=∠DCE,
∵∠DCE+∠DEC=90°,
∴∠AE0+∠DEC=90°,
∴∠OEC=90 °,
∴直线CE与⊙O相切.
BC=2,∴AB=BCtan∠ACB=
AC= .
又∵∠ACB=∠DCE ∴tan∠DCE= ,
设⊙O的半径为r,则在Rt△COE中,
解得:r= .
(2)∵tan∠ACB=
∴DE=DC?tan∠DCE=1,
在Rt△CDE中,CE=
得
,
,
由
6.如图,AB是半圆的直径,O为圆心,AD,BD是半圆的弦,且∠PDA=∠PBD.
(1)判断直线PD是否为⊙O的切线,并说明理由.
(2)如果∠BDE=60°, ,求PA的长.
(1)PD是⊙O的切线.
连接OD,∵OB=OD,
∴∠ODB=∠PBD.
又∵∠PDA=∠PBD.∴∠ODB=∠PDA.
又∵AB是半圆的直径,∴∠ADB=90°.
即∠ODB+∠ODA=90°. ∴∠ODA+∠PDA=90°,
即OD⊥PD.∴PD是⊙O的切线.
(2)∵∠BDE=60°,∠ODE=90°,∠ADB=90°,
∴∠ODB=30°,∠ODA=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴∠POD=60°.
∴∠P=∠PDA=30°.
在Rt△PDO中,设OD=x,
∴x1=1,x2=-1(不合题意,舍去)
∴PA=1.
∴
7.如图,在△ABC中,AB =AC,0是BC的中点,AC与半圆0相切于点D.(1)求证:AB是半圆0所在圆的切线;(2)若cos∠ABC= ,AB=12,求半圆0所在圆的半径.
如图,在△ABC中,AB =AC,0是BC的中点,AC与半圆0相切于点D.(1)求证:AB是半圆0所在圆的切线;(2)若cos∠ABC= ,AB=12,求半圆0所在圆的半径.
8.如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC、AB分别相交于点D、F,且DE=EF. (1)求证:∠C=90°;
解:(1)连接OE、BE,∵DE=EF,∴
∴∠OBE=∠DBE,∵OE=OB,∴∠OEB=∠OBE,∴∠OEB=∠DBE,∴OE∥BC,∵⊙O与边AC相切于点E,∴OE⊥AC,∴BC⊥AC,∴∠C=90°;
8.如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC、AB分别相交于点D、F,且DE=EF.
9.如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC. (1)求证:∠BAC=∠CBP; (2)求证:PB2=PC·PA; (3)当AC=6,CP=3时,求sin∠PAB的值.
(1)证明:∵AB是⊙O的直径;∴∠ACB=90°,
∴∠A+∠ABC=90°,∵PB与⊙O相切于点B,
∴∠CBP+∠ABC=90°,∴∠BAC=∠CBP;
9.如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC. (1)求证:∠BAC=∠CBP; (2)求证:PB2=PC·PA; (3)当AC=6,CP=3时,求sin∠PAB的值.
10.如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD. (1)求证:△CDE∽△CAD; (2)若AB=2,AC= ,求AE的长.
11.如图,在△ABC中,内切圆⊙I和边BC、CA、AB分别切于点D、E、F. (1)若AB=6,AC=8,BC=10,试求内切圆的面积; (2)若∠A=80°,试求∠EDF的度数,并探求∠A与∠EDF有何关系? (3)△DFE一定是锐角三角形吗?为什么?
11.如图,在△ABC中,内切圆⊙I和边BC、CA、AB分别切于点D、E、F. (1)若AB=6,AC=8,BC=10,试求内切圆的面积; (2)若∠A=80°,试求∠EDF的度数,并探求∠A与∠EDF有何关系? (3)△DFE一定是锐角三角形吗?为什么?
(3)由(2)知,∠FDE、∠DFE、∠FED都为锐角,
∴△DEF一定是锐角三角形.
12.如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D,连接BE,过点O作OC∥BE交切线DE于点C,连接AC. (1)求证:AC是⊙O的切线; (2)若BD=OB=4,求弦AE的长.
(1)证明:连接OE.∵CD与圆O相切,∴OE⊥CD,
∴∠CEO=90°,∵BE∥OC,∴∠AOC=∠OBE,∠COE=∠OEB,∵OB=OE,∴∠OBE=∠OEB,∴∠AOC=∠COE,又由OC=OC,AO=OE,∴△AOC≌△EOC(SAS),∴∠CAO=∠CEO=90°,则AC与圆O相切;
12.如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D,连接BE,过点O作OC∥BE交切线DE于点C,连接AC. (1)求证:AC是⊙O的切线; (2)若BD=OB=4,求弦AE的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
第三章 圆
3.6 直线和圆的位置关系
第2课时 切线的判定与三角形的内切圆
B
●O
A
┓
d
α
┏
d
α
d
┓
l
(1)圆心O到直线l的距离d
从等于半径开始,慢慢变短直到0,
然后又开始变长直到等于半径。
直线l与☉O的位置关系从相切到相交,最后到相切。
如图,AB是☉0的直径,直线l经过点A,AB与AC的夹角为∠α
(1)观察直线l转动,点O到l的距离d如何变化?直线l与☉O的位置关系如何变化?
(2)当∠α等于多少度时,点0到l的距离d等于半径r?此时,直线l与☉0有怎样的位置关系?为什么?
C
D
(2)当∠a=90?
相切
α
过半径外端且垂直于半径的直线是圆的切线.
C
D
B
●O
A
∵AB是⊙O的直径,直线CD经过A点,且CD⊥AB,
∴ CD是⊙O的切线.
这个定理实际上就是
d=r 直线和圆相切的另一种说法.
切线的判定定理
下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A
O.
A
B
A
O
(1)
(2)
(3)
(1)不是,因为没有垂直.
(2),(3)不是,因为没有经过半径的外端点A.
在此定理中,“经过半径的外端”和“垂直于这条半径”,两个条件缺一不可,否则就不是圆的切线.
注意
判断
例1 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB.求证:直线AB是⊙O的切线.
O
B
A
C
证明:连接OC.
∵ OA=OB,CA=CB,
∴ OC是等腰△OAB底边AB上的中线.
∴ AB⊥OC.
∵ OC是⊙O的半径,
∴ AB是⊙O的切线.
作法:
1.作∠B和∠C的平分线BM和CN,交点为O.
2.过点O作OD⊥BC.垂足为D.
3.以O为圆心,OD为半径作圆O.
☉O就是所求的圆.
M
N
D
例2 如何作圆,使它和已知三角形的各边都相切?
已知:△ABC.
求作:和△ABC的各边都相切的圆O.
由作图过程可知,BE和CF只有一个交点O,并且O到△ABC三边的距离相等、因此和三角形二边都相切的圆可以作出一个,并且只能作出一个,这个圆叫做三角形的内切圆
D
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
3.三角形的内心到三角形的三边的距离相等.
4.三角形的内心就是三角形的三条角平分线的交点.
名称
确定方法
图形
性质
外心:三角形外接圆的圆心
内心:三角形内切圆的圆心
三角形三边中垂线的交点
1.OA=OB=OC
2.外心不一定在三角形的内部.
三角形三条角平分线的交点
1.到三边的距离相等;
2.OA、OB、OC分别
平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.
A
B
O
A
B
C
O
练习1: △ABC中,⊙O是△ABC的内切圆,∠ A=70°,
求∠ BOC的度数。
A
B
C
O
∴∠ BOC=180°-(∠ OBC+∠OCB)
=180°- ( ∠ABC +∠ACB)
=180° - ×110°
= 125°.
2.如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.
证明:连接OM,过点O作ON⊥CD于点N,
∵⊙O与BC相切于点M,
∴OM⊥BC,OM=OA
又∵O为正方形ABCD对角线AC上一点,
∴OM=MC,又ON⊥CD,
∴四边形OMCNO为正方形。
∴ON=0A,∴CD与⊙O相切.
M
N
课后作业
1.已知:△ABC内接于☉O,过点A作直线EF.
(1)如图1,AB为直径,要使EF为☉O的切线,还需添加的条件是(只需写出两种情况): ① _________ ;② _____________ .
(2)如图2,AB是非直径的弦,∠CAE=∠B,求证:EF是☉O的切线.
BA⊥EF
∠CAE=∠B
A
F
E
O
A
F
E
O
B
C
B
C
图1
图2
证明:连接AO并延长交☉O于D,连接CD,则AD为☉O的直径.
∴ ∠D+ ∠DAC=90 °,
∴EF是☉O的切线.
∴ ∠DAC+ ∠EAC=90°,
∴ ∠D= ∠CAE,
又∵ ∠CAE= ∠B,
∴ ∠D= ∠B,
∵ ∠D与∠B同对
D
2.如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=AB·AE,求证:DE是⊙O的切线.
∵AD2=AB·AE,∠BAD=∠DAE,
∴△BAD∽△DAE,∴∠ADB=∠E.
又∵∠ADB=∠ACB,∴∠ACB=∠E,BC∥DE,
∴∠CDE=∠BCD=∠BAD=∠DAC,
又∵∠CAF=∠CDF,
∴∠FDE=∠CDE+∠CDF=∠DAC+∠CAF=∠DAF=90°,
故DE是⊙O的切线.
证明:连接DC,DO,并延长DO交⊙O于F,连接AF.
F
3.如图,已知E是△ABC的内心,∠A的平分线交BC于点F,且与△ABC的外接圆相交于点D.
(1)证明:∵E是△ABC的内心,
∴∠ABE=∠CBE,∠BAD=∠CAD.
又∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
∴∠CBE+∠CBD=∠ABE+∠BAD.
即∠DBE=∠DEB,
故BD=ED;
(1)求证:BD=ED;
(2)若AD=8cm,DF∶FA=1∶3.求DE的长.
(2)解:∵AD=8cm,DF∶FA=1∶3,
∴DF= AD= ×8=2(cm).
∵∠CBD=∠BAD,∠D=∠D,∴△BDF∽△ADB,∴ ,
∴BD2=AD·DF=8×2=16,
∴BD=4cm,
又∵BD=DE,
3.如图,已知E是△ABC的内心,∠A的平分线交BC于点F,且与△ABC的外接圆相交于点D.
∴DE=4cm.
4.如图,以△ABC的BC边上一点0为圆心的圆,经过AB两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于点F,AC=FC(1)求证:AC是☉0的切线;(2)已知圆的半径R=5,EF=3,求DF的长.
(2)解:在Rt△OFD中,OF =5-3=2,0D =5,
(1)证明:连接OD,OA ,
∵D是BE的中点,BE是直径,
∴OD⊥BE,
∵∠ODF+∠OFD=90°,
∴0A=0D,
∴ ∠OAD =∠ODA,
∵AC=FC,
∴∠CAF=∠CFA=∠OFD.
∴∠0AC=90°
∴AC是☉0的切线;
5.(德化·中考)如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE.
(1)判断直线CE与⊙O的位置关系,并证明你的结论.
(2)若tan∠ACB= ,BC=2,
求⊙O的半径.
E
A
B
C
D
F
O
解:(1)直线CE与⊙O相切.
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC ,
又 ∵∠ACB=∠DCE,
∴∠DAC=∠DCE,连接OE,则∠DAC=∠AEO=∠DCE,
∵∠DCE+∠DEC=90°,
∴∠AE0+∠DEC=90°,
∴∠OEC=90 °,
∴直线CE与⊙O相切.
BC=2,∴AB=BCtan∠ACB=
AC= .
又∵∠ACB=∠DCE ∴tan∠DCE= ,
设⊙O的半径为r,则在Rt△COE中,
解得:r= .
(2)∵tan∠ACB=
∴DE=DC?tan∠DCE=1,
在Rt△CDE中,CE=
得
,
,
由
6.如图,AB是半圆的直径,O为圆心,AD,BD是半圆的弦,且∠PDA=∠PBD.
(1)判断直线PD是否为⊙O的切线,并说明理由.
(2)如果∠BDE=60°, ,求PA的长.
(1)PD是⊙O的切线.
连接OD,∵OB=OD,
∴∠ODB=∠PBD.
又∵∠PDA=∠PBD.∴∠ODB=∠PDA.
又∵AB是半圆的直径,∴∠ADB=90°.
即∠ODB+∠ODA=90°. ∴∠ODA+∠PDA=90°,
即OD⊥PD.∴PD是⊙O的切线.
(2)∵∠BDE=60°,∠ODE=90°,∠ADB=90°,
∴∠ODB=30°,∠ODA=60°.
∵OA=OD,
∴△AOD是等边三角形.
∴∠POD=60°.
∴∠P=∠PDA=30°.
在Rt△PDO中,设OD=x,
∴x1=1,x2=-1(不合题意,舍去)
∴PA=1.
∴
7.如图,在△ABC中,AB =AC,0是BC的中点,AC与半圆0相切于点D.(1)求证:AB是半圆0所在圆的切线;(2)若cos∠ABC= ,AB=12,求半圆0所在圆的半径.
如图,在△ABC中,AB =AC,0是BC的中点,AC与半圆0相切于点D.(1)求证:AB是半圆0所在圆的切线;(2)若cos∠ABC= ,AB=12,求半圆0所在圆的半径.
8.如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC、AB分别相交于点D、F,且DE=EF. (1)求证:∠C=90°;
解:(1)连接OE、BE,∵DE=EF,∴
∴∠OBE=∠DBE,∵OE=OB,∴∠OEB=∠OBE,∴∠OEB=∠DBE,∴OE∥BC,∵⊙O与边AC相切于点E,∴OE⊥AC,∴BC⊥AC,∴∠C=90°;
8.如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC、AB分别相交于点D、F,且DE=EF.
9.如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC. (1)求证:∠BAC=∠CBP; (2)求证:PB2=PC·PA; (3)当AC=6,CP=3时,求sin∠PAB的值.
(1)证明:∵AB是⊙O的直径;∴∠ACB=90°,
∴∠A+∠ABC=90°,∵PB与⊙O相切于点B,
∴∠CBP+∠ABC=90°,∴∠BAC=∠CBP;
9.如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC. (1)求证:∠BAC=∠CBP; (2)求证:PB2=PC·PA; (3)当AC=6,CP=3时,求sin∠PAB的值.
10.如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD. (1)求证:△CDE∽△CAD; (2)若AB=2,AC= ,求AE的长.
11.如图,在△ABC中,内切圆⊙I和边BC、CA、AB分别切于点D、E、F. (1)若AB=6,AC=8,BC=10,试求内切圆的面积; (2)若∠A=80°,试求∠EDF的度数,并探求∠A与∠EDF有何关系? (3)△DFE一定是锐角三角形吗?为什么?
11.如图,在△ABC中,内切圆⊙I和边BC、CA、AB分别切于点D、E、F. (1)若AB=6,AC=8,BC=10,试求内切圆的面积; (2)若∠A=80°,试求∠EDF的度数,并探求∠A与∠EDF有何关系? (3)△DFE一定是锐角三角形吗?为什么?
(3)由(2)知,∠FDE、∠DFE、∠FED都为锐角,
∴△DEF一定是锐角三角形.
12.如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D,连接BE,过点O作OC∥BE交切线DE于点C,连接AC. (1)求证:AC是⊙O的切线; (2)若BD=OB=4,求弦AE的长.
(1)证明:连接OE.∵CD与圆O相切,∴OE⊥CD,
∴∠CEO=90°,∵BE∥OC,∴∠AOC=∠OBE,∠COE=∠OEB,∵OB=OE,∴∠OBE=∠OEB,∴∠AOC=∠COE,又由OC=OC,AO=OE,∴△AOC≌△EOC(SAS),∴∠CAO=∠CEO=90°,则AC与圆O相切;
12.如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D,连接BE,过点O作OC∥BE交切线DE于点C,连接AC. (1)求证:AC是⊙O的切线; (2)若BD=OB=4,求弦AE的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
