3.7 切线长定理 课件(共25张PPT)
文档属性
| 名称 | 3.7 切线长定理 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 21:20:26 | ||
图片预览




文档简介
数学北师大版
九年级
3.7切线长定理
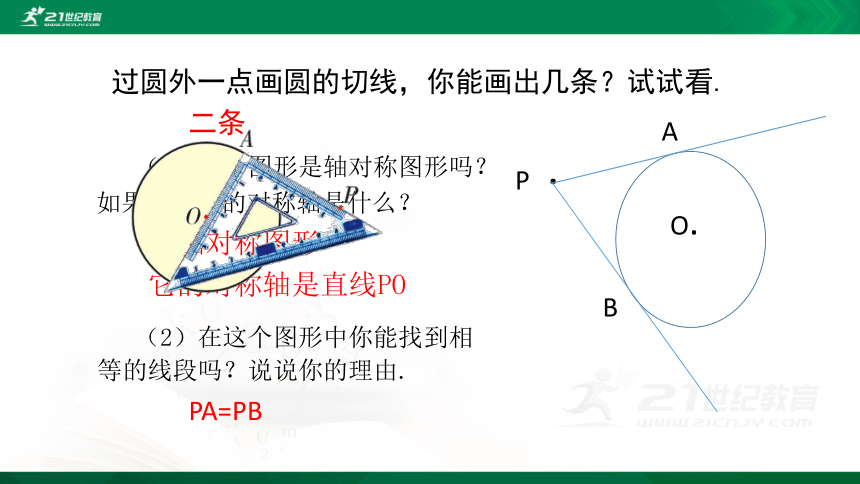
过圆外一点画圆的切线,你能画出几条?试试看.
.
P
A
B
二条
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)在这个图形中你能找到相等的线段吗?说说你的理由.
O.
是轴对称图形
它的对称轴是直线PO
PA=PB
切线长定理 过圆外一点所画的圆的两条切线长相等.
过圆外一点画圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
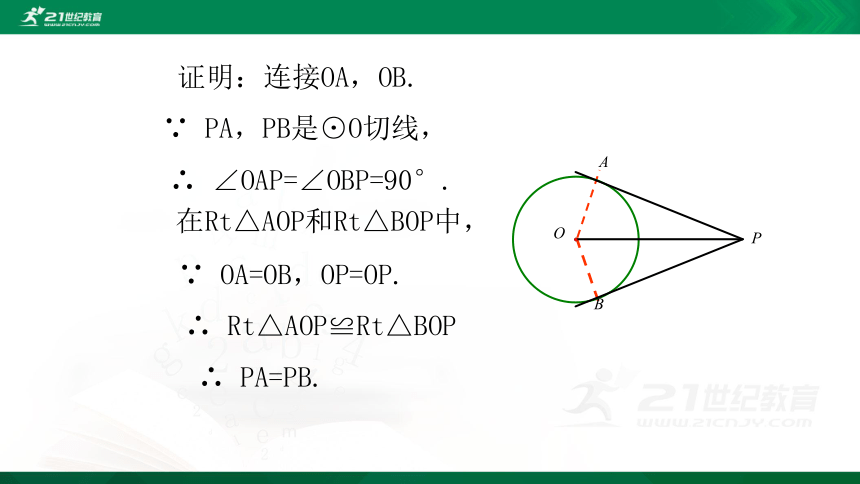
已知:如图3-31,P为⊙O外一点,PA,PB为⊙O的切线,A,B为切点.
我们来证明切线长定理.
求证:PA=PB.
P
O
A
B
∴ Rt△AOP≌Rt△BOP
证明:连接OA,OB.
∵ PA,PB是⊙O切线,
∴ ∠OAP=∠OBP=90°.
∵ OA=OB,OP=OP.
∴ PA=PB.
在Rt△AOP和Rt△BOP中,
P
O
A
B
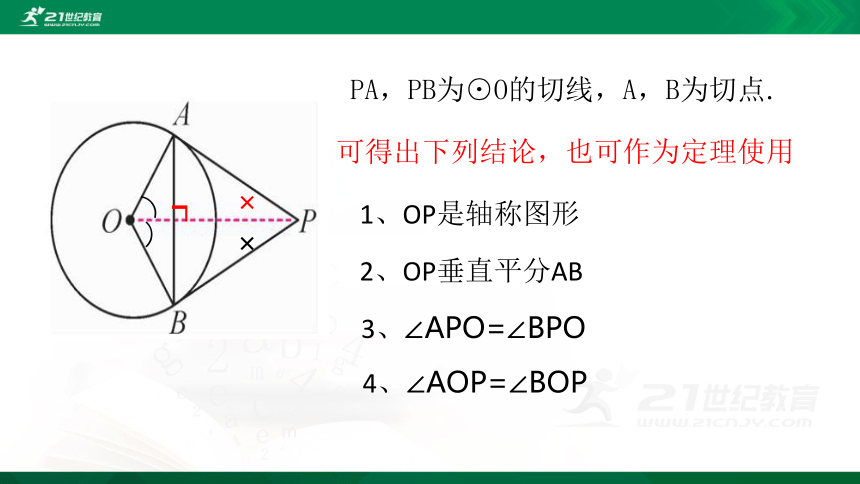
PA,PB为⊙O的切线,A,B为切点.
可得出下列结论,也可作为定理使用
1、OP是轴称图形
2、OP垂直平分AB
3、∠APO=∠BPO
×
×
4、∠AOP=∠BOP
┑
╮
╮
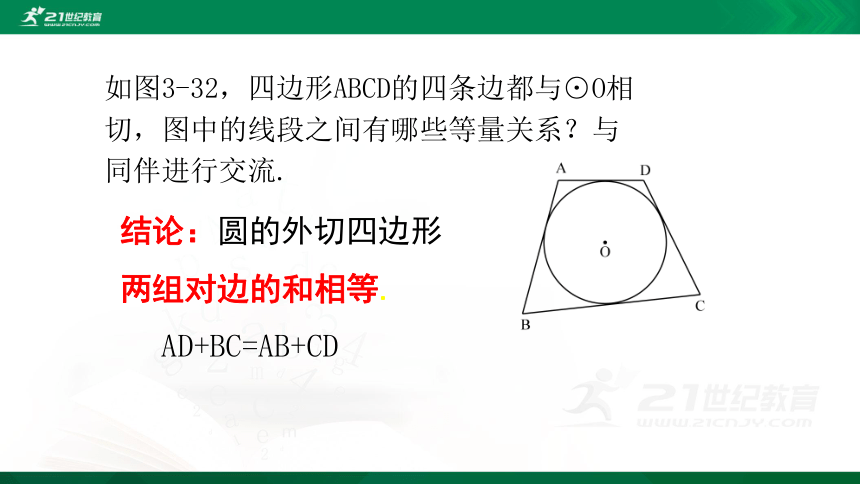
如图3-32,四边形ABCD的四条边都与⊙O相切,图中的线段之间有哪些等量关系?与同伴进行交流.
结论:圆的外切四边形
两组对边的和相等.
AD+BC=AB+CD
例 如图3-33,Rt△ABC的两条直角边AC=10,BC=24,⊙O是△ABC的内切圆,切点分别为D,E,F,求⊙O的半径.
解:连接OD,OE,OF,设OD=r.
在Rt△ABC中, AC=10,BC=24,
∵⊙O分别与AB,BC,CA相切于点D,E,F,
A
B
C
D
E
F
∴ OD⊥AB,OE⊥BC,OF⊥AC,BE=BD,AF=AD,CE=CF.
又∵ ∠C=90°,
∴ 四边形OECF为正方形.
∴ EC=FC=r.
∴ BE=24-r,AF=10-r.
∴ AB=BD+AD=BE+AF=34-2r=26.
∴ r=4,
即⊙O的半径为4.
A
B
C
E
F
例 如图3-33,Rt△ABC的两条直角边AC=10,BC=24,⊙O是△ABC的内切圆,切点分别为D,E,F,求⊙O的半径.
解法二:连接OD,OE,OF,设OD=r.
在Rt△ABC中, AC=10,BC=24,
A
B
C
D
E
F
CB×AC= r×AB+ r×BC+ r×AC
∴CB×AC= r×AB+ r×BC+ r×AC
A
B
C
10×24=r×10+r×24+r×26
∴ r=4,
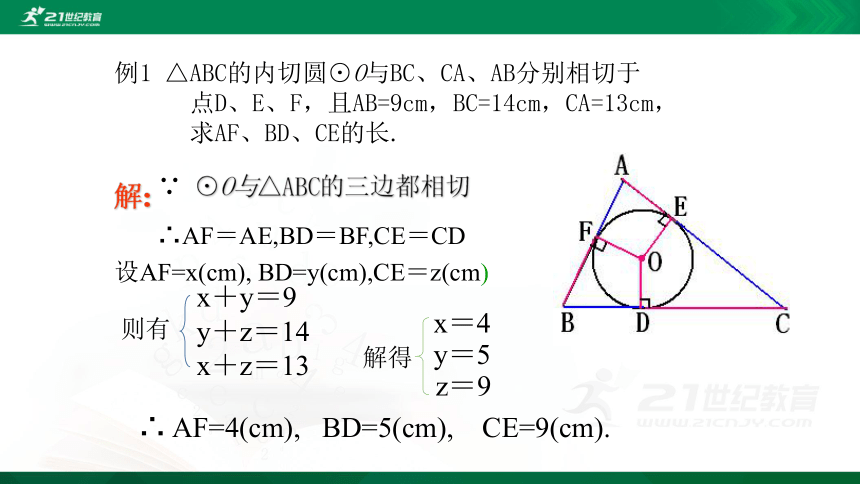
例1 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.
解:
设AF=x(cm), BD=y(cm),CE=z(cm)
∴ AF=4(cm), BD=5(cm), CE=9(cm).
∵ ⊙O与△ABC的三边都相切
∴AF=AE,BD=BF,CE=CD
则有
x+y=9
y+z=14
x+z=13
解得
x=4
y=5
z=9
O
P
A
B
C
E
D
⑴ △PDE的周长是 ;
例2 如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.已知PA=7,∠P=40°.则
⑵ ∠DOE= ____ .
解析:∵DC、DA是☉O的两条切线,点C、A是切点,∴DC=DA.
同理可得CE=EB.∵PA、PB是☉O的两条切线,点A、B是切点,∴PA=PB=7.
l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
O
P
A
B
C
E
D
∵OA=OC,OD=OD,∴△AOD≌△COD,
∴∠DOC=∠DOA= ∠AOC.
同理可得∠COE= ∠COB.
∠DOE=∠DOC+∠COE= (∠AOC+
∠COB)=70°.
连接OA、OB、OC、OD和OE.
∠PAO=∠PBO=90°. ∠AOB=360°-∠PAO-∠PBO-∠P=140°.
本课小结
切线的6个性质:
(1)切线和圆只有一个公共点.
(2)切线和圆心的距离等于圆的半径.
(3)切线垂直于过切点的半径.
(4)经过圆心垂直于切线的直线必过切点.
(5)经过切点垂直于切线的直线必过圆心.
(6)切线长定理.
课后作业
1.如图,AB, BC, CD分别与☉0相切于点E,F,G,且AB// CD. BO =6COcm,CO=8cm.
(1 )求证:BO⊥CO;
(2)求BE和CG的长.
1.如图,AB, BC, CD分别与☉0相切于点E,F,G,且AB// CD. BO =6COcm,CO=8cm.
(2)求BE和CG的长.
2. 已知△ABC的内切圆☉0与边AB, BC,AC分别相切于点D,E,F,若EF= DE,如图1(1 )判断△ABC的形状,并证明你的结论;(2)设AE与DF'相交于点M,如图2,AF'=2FC=4,求AM的长.
2. 已知△ABC的内切圆☉0与边AB, BC,AC分别相切于点D,E,F,若EF= DE,如图1(1 )判断△ABC的形状,并证明你的结论;(2)设AE与DF'相交于点M,如图2,AF'=2FC=4,求AM的长.
(2)∵AB,BC,AC与☉0相切于点D,E,F. ∴AF=AD,CF=CE,∠FAM =∠DAM
.∴AM⊥DF.由(1)可得AE⊥BC,∴FM//CE.
∵AF=2FC =4,
∴CE =FC =2.
AC =6.
3.如图,正方形ABCD的边长为4 cm,以BC为直径作圆,再过A点作圆的切线,交DC于E,切点为F,
求:(1)△ADE的面积;(2)BF的长.
3.如图,正方形ABCD的边长为4 cm,以BC为直径作圆,再过A点作圆的切线,交DC于E,切点为F,求:(1)△ADE的面积;(2)BF的长.
4.如图,PA, PB分别切☉0于A,B两点,BC是☉O的直径,连接AB,OP,AC.求证:∠ APB=2∠ABC.
证明:连接OA. ∵PA, PB切☉O于A, B,
OA,OB是半径,∴∠0AP=∠OBP=90°. ∵OA=OB,∴∠APO=∠BPO= APB.
又∵PA=PB, ∴OP⊥AB,
∴∠BEO= 90°=∠ABC+ L BOP.
又∵∠OBP=90°=∠0PB十∠BOP,
∴∠A BC =∠OPB = ∠APB,
即∠APB =2∠ABC.
5.如图,PA,PB分别与☉O相切于点A,B,点M在PB上,且OM// AP,MN_上AP,垂足为N.(1)求证:OM=AN;(2)若☉O的半径R=3,PA=9,求OM的长.
,
(1)连接OA,则OA⊥AP
∵MN|AP,
∴MN//OA,
∴OM// AP,
∴四边形ANMO是矩形
∴OM= AN;
(2)连接OB,则OB┴BP
∵OA= MN,0A=OB,OM // AP,
∴OB=MN,∠OMB= ∠NPM,
∴Rt△OBM≌Rt△MNP,
∴OM=MP.
设OM=x,则NP=9-x.
在Rt△MNP中,x2=32+(9-x)2,
∴x=5,∴OM=5.
6.如图,AB是☉O的直径,BC⊥AB于点B,连接OC交☉O于点E,弦AD//OC,弦DF⊥AB于点G.(1)求证:点E是BD弧的中点;(2)求证:CD是☉0的切线;(3)若AD=12,☉0的半径为10,求弦DF的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
3.7切线长定理
过圆外一点画圆的切线,你能画出几条?试试看.
.
P
A
B
二条
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)在这个图形中你能找到相等的线段吗?说说你的理由.
O.
是轴对称图形
它的对称轴是直线PO
PA=PB
切线长定理 过圆外一点所画的圆的两条切线长相等.
过圆外一点画圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.
已知:如图3-31,P为⊙O外一点,PA,PB为⊙O的切线,A,B为切点.
我们来证明切线长定理.
求证:PA=PB.
P
O
A
B
∴ Rt△AOP≌Rt△BOP
证明:连接OA,OB.
∵ PA,PB是⊙O切线,
∴ ∠OAP=∠OBP=90°.
∵ OA=OB,OP=OP.
∴ PA=PB.
在Rt△AOP和Rt△BOP中,
P
O
A
B
PA,PB为⊙O的切线,A,B为切点.
可得出下列结论,也可作为定理使用
1、OP是轴称图形
2、OP垂直平分AB
3、∠APO=∠BPO
×
×
4、∠AOP=∠BOP
┑
╮
╮
如图3-32,四边形ABCD的四条边都与⊙O相切,图中的线段之间有哪些等量关系?与同伴进行交流.
结论:圆的外切四边形
两组对边的和相等.
AD+BC=AB+CD
例 如图3-33,Rt△ABC的两条直角边AC=10,BC=24,⊙O是△ABC的内切圆,切点分别为D,E,F,求⊙O的半径.
解:连接OD,OE,OF,设OD=r.
在Rt△ABC中, AC=10,BC=24,
∵⊙O分别与AB,BC,CA相切于点D,E,F,
A
B
C
D
E
F
∴ OD⊥AB,OE⊥BC,OF⊥AC,BE=BD,AF=AD,CE=CF.
又∵ ∠C=90°,
∴ 四边形OECF为正方形.
∴ EC=FC=r.
∴ BE=24-r,AF=10-r.
∴ AB=BD+AD=BE+AF=34-2r=26.
∴ r=4,
即⊙O的半径为4.
A
B
C
E
F
例 如图3-33,Rt△ABC的两条直角边AC=10,BC=24,⊙O是△ABC的内切圆,切点分别为D,E,F,求⊙O的半径.
解法二:连接OD,OE,OF,设OD=r.
在Rt△ABC中, AC=10,BC=24,
A
B
C
D
E
F
CB×AC= r×AB+ r×BC+ r×AC
∴CB×AC= r×AB+ r×BC+ r×AC
A
B
C
10×24=r×10+r×24+r×26
∴ r=4,
例1 △ABC的内切圆⊙O与BC、CA、AB分别相切于
点D、E、F,且AB=9cm,BC=14cm,CA=13cm,
求AF、BD、CE的长.
解:
设AF=x(cm), BD=y(cm),CE=z(cm)
∴ AF=4(cm), BD=5(cm), CE=9(cm).
∵ ⊙O与△ABC的三边都相切
∴AF=AE,BD=BF,CE=CD
则有
x+y=9
y+z=14
x+z=13
解得
x=4
y=5
z=9
O
P
A
B
C
E
D
⑴ △PDE的周长是 ;
例2 如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.已知PA=7,∠P=40°.则
⑵ ∠DOE= ____ .
解析:∵DC、DA是☉O的两条切线,点C、A是切点,∴DC=DA.
同理可得CE=EB.∵PA、PB是☉O的两条切线,点A、B是切点,∴PA=PB=7.
l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
O
P
A
B
C
E
D
∵OA=OC,OD=OD,∴△AOD≌△COD,
∴∠DOC=∠DOA= ∠AOC.
同理可得∠COE= ∠COB.
∠DOE=∠DOC+∠COE= (∠AOC+
∠COB)=70°.
连接OA、OB、OC、OD和OE.
∠PAO=∠PBO=90°. ∠AOB=360°-∠PAO-∠PBO-∠P=140°.
本课小结
切线的6个性质:
(1)切线和圆只有一个公共点.
(2)切线和圆心的距离等于圆的半径.
(3)切线垂直于过切点的半径.
(4)经过圆心垂直于切线的直线必过切点.
(5)经过切点垂直于切线的直线必过圆心.
(6)切线长定理.
课后作业
1.如图,AB, BC, CD分别与☉0相切于点E,F,G,且AB// CD. BO =6COcm,CO=8cm.
(1 )求证:BO⊥CO;
(2)求BE和CG的长.
1.如图,AB, BC, CD分别与☉0相切于点E,F,G,且AB// CD. BO =6COcm,CO=8cm.
(2)求BE和CG的长.
2. 已知△ABC的内切圆☉0与边AB, BC,AC分别相切于点D,E,F,若EF= DE,如图1(1 )判断△ABC的形状,并证明你的结论;(2)设AE与DF'相交于点M,如图2,AF'=2FC=4,求AM的长.
2. 已知△ABC的内切圆☉0与边AB, BC,AC分别相切于点D,E,F,若EF= DE,如图1(1 )判断△ABC的形状,并证明你的结论;(2)设AE与DF'相交于点M,如图2,AF'=2FC=4,求AM的长.
(2)∵AB,BC,AC与☉0相切于点D,E,F. ∴AF=AD,CF=CE,∠FAM =∠DAM
.∴AM⊥DF.由(1)可得AE⊥BC,∴FM//CE.
∵AF=2FC =4,
∴CE =FC =2.
AC =6.
3.如图,正方形ABCD的边长为4 cm,以BC为直径作圆,再过A点作圆的切线,交DC于E,切点为F,
求:(1)△ADE的面积;(2)BF的长.
3.如图,正方形ABCD的边长为4 cm,以BC为直径作圆,再过A点作圆的切线,交DC于E,切点为F,求:(1)△ADE的面积;(2)BF的长.
4.如图,PA, PB分别切☉0于A,B两点,BC是☉O的直径,连接AB,OP,AC.求证:∠ APB=2∠ABC.
证明:连接OA. ∵PA, PB切☉O于A, B,
OA,OB是半径,∴∠0AP=∠OBP=90°. ∵OA=OB,∴∠APO=∠BPO= APB.
又∵PA=PB, ∴OP⊥AB,
∴∠BEO= 90°=∠ABC+ L BOP.
又∵∠OBP=90°=∠0PB十∠BOP,
∴∠A BC =∠OPB = ∠APB,
即∠APB =2∠ABC.
5.如图,PA,PB分别与☉O相切于点A,B,点M在PB上,且OM// AP,MN_上AP,垂足为N.(1)求证:OM=AN;(2)若☉O的半径R=3,PA=9,求OM的长.
,
(1)连接OA,则OA⊥AP
∵MN|AP,
∴MN//OA,
∴OM// AP,
∴四边形ANMO是矩形
∴OM= AN;
(2)连接OB,则OB┴BP
∵OA= MN,0A=OB,OM // AP,
∴OB=MN,∠OMB= ∠NPM,
∴Rt△OBM≌Rt△MNP,
∴OM=MP.
设OM=x,则NP=9-x.
在Rt△MNP中,x2=32+(9-x)2,
∴x=5,∴OM=5.
6.如图,AB是☉O的直径,BC⊥AB于点B,连接OC交☉O于点E,弦AD//OC,弦DF⊥AB于点G.(1)求证:点E是BD弧的中点;(2)求证:CD是☉0的切线;(3)若AD=12,☉0的半径为10,求弦DF的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
