3.9 弧长及扇形的面积 课件(共30张PPT)
文档属性
| 名称 | 3.9 弧长及扇形的面积 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-02-28 21:31:53 | ||
图片预览








文档简介
数学北师大版
九年级
3.9 弧长及扇形的面积
情景导入
如图,某传送带的一个转动伦的半径为10cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
n°圆心角所对的弧长
合作探究
∵圆的周长是C=2πR它所对的中心角是360?
那么1°的圆心角所对弧长
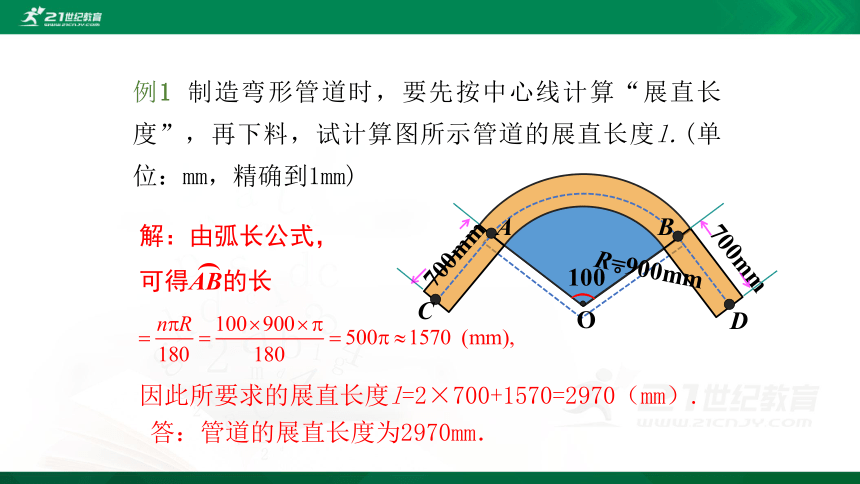
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度l.(单位:mm,精确到1mm)
解:由弧长公式,可得AB的长
因此所要求的展直长度l=2×700+1570=2970(mm).
答:管道的展直长度为2970mm.
700mm
700mm
R=900mm
(
100 °
A
C
B
D
O
(
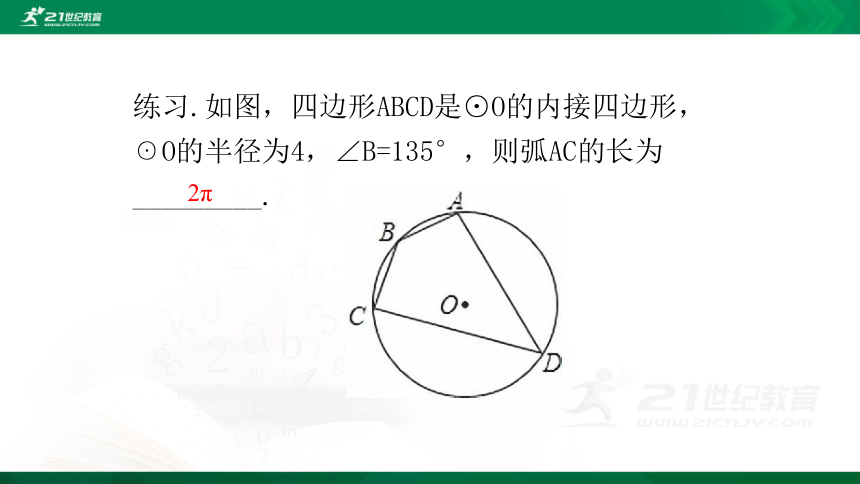
练习.如图,四边形ABCD是⊙O的内接四边形,☉O的半径为4,∠B=135°,则弧AC的长为_________.
2π
上面图形BAC是扇形吗?
.o
A
B
C
r
B
A
C
.
B
C
A
√
×
×
半径为R的圆的面积S=πR2 ,由于圆所对的中心角是360?,
那么中心角是n?的扇形的面积应是
问题:扇形的弧长公式与面积公式有联系吗?
想一想 扇形的面积公式与什么公式类似?
A
B
O
O
例1 如图,已知圆O的半径12cm,圆心角∠AOB=120o,求AB的长(结果精确到0.1cm2)和扇形OAB的面积(结果精确到0.1cm2).
(
解:AB=
(
为什么这二种解法会产生答案不同,主要是弧长计算时已经是约数了,如果要用第二种解法,弧长要么写成分数,要么多精确一位。
例2 如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm)
O .
B
A
C
解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵ OC=0.6, DC=0.3,
∴ OD=OC- DC=0.3,
∴ OD=DC.
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而 ∠AOD=60?, ∠AOB=120?.
有水部分的面积:
S=S扇形OAB - S ΔOAB
┑
D
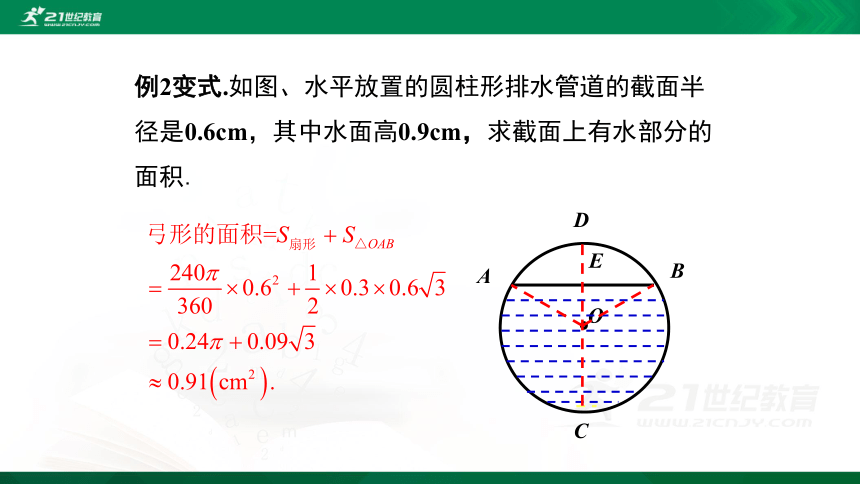
例2变式.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
O
A
B
D
C
E
O
O
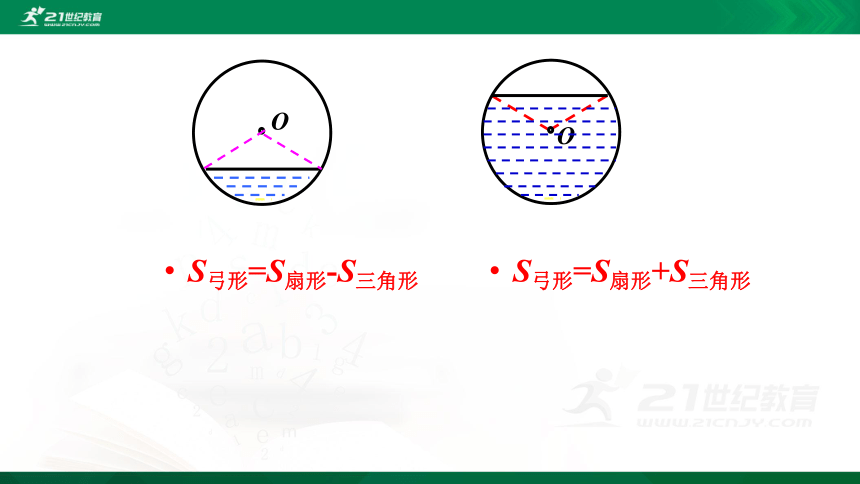
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
1. (2018·广东)如图,矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为 .(结果保留π)
割补思想
S阴=S?BCD-(S正方形OECD-S扇形OED)
=π
2.将△ABC绕点B逆时针旋转到△A'BC',使A、B、C'在同一直线上,∠BCA=90°,∠BAC=30°,AB =4 cm,则图2中阴影部分面积为__________cm2
S阴=S△A′BC′+S扇形A′BA-
S扇形BCC′-S△ABC=S扇形A′BA-
S扇形BCC′=4π
弧长
扇形
阴影部分面积
求法:整体思想
弓形
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
本课小结
课后作业
1.如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是A、B、C,如果AB=1,求曲线CDEF的长.
解析:连接OB、OC,
∵AB是⊙O的切线,∴AB⊥BO.
∵∠A=30°,∴∠AOB=60°.
∵BC∥AO,∴∠OBC=∠AOB=60°.
在等腰△OBC中,
∠BOC=180°-2∠OBC=180°-2×60°=60°.
∴BC的长为 =2π(cm).
故答案为2π.
2.如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥AO.若∠A=30°,则劣弧BC的长为________cm.
︵
︵
2π
3.(淮安中考)如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点. (1)试判断直线DE与⊙O的位置关系,并说明理由; (2)若⊙O的半径为2,∠B=50°,AC=4.8,求图中阴影部分的面积.
∵点E是AC的中点,O点为AB的中点,∴OE∥BC,∴∠1=∠B,∠2=∠3,∵OB=OD,∴∠B=∠3,∴∠1=∠2,AO=DO,OE=OE(∠1=∠2),∴△AOE≌△DOE,∴∠ODE=∠OAE=90°,∴OD⊥DE,∴DE为⊙O的切线;
解:(1)直线DE与⊙O相切.
理由如下:连接OE、OD,如图,
∵AC是⊙O的切线,∴AB⊥AC,∴∠OAC=90°,
3.(淮安中考)如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点. (1)试判断直线DE与⊙O的位置关系,并说明理由; (2)若⊙O的半径为2,∠B=50°,AC=4.8,求图中阴影部分的面积.
4.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF. (1)求证:OF∥BC; (2)求证:△AFO≌△CEB; (3)若EB=5cm,CD=10 cm,设OE=x,求x的值及阴影部分的面积.
(1)证明:∵AB是⊙O直径,∴∠ACB=90°,
又OF⊥AC,∴CB∥OF;
(2)证明:在△CEB和△AFO中,BE=OF,
∠B=∠AOF,∠CEB=∠AFO=90°,∴△AFO≌△CEB;
4.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF. (1)求证:OF∥BC; (2)求证:△AFO≌△CEB; (3)若EB=5cm,CD=10 cm,设OE=x,求x的值及阴影部分的面积.
5. (2018·河南)如图,在△ABC中,∠ACB=90°,AC=BC=2.将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′,其中点B的运动路径为(BB′),则图中阴影部分的面积为 .
︵
6. (2018·江西)图①是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框上,通过推动左侧活页门开关.图②是其俯视简化示意图,已知轨道AB=120 cm,两扇活页门的宽OC=OB=60 m,点B固定,当点C在AB上左右运动时,OC与OB的长度不变.(所有的结果保留小数点后一位)(1)若∠OBC=50°,求AC的长;
(2)当点C从点A向右运动60 cm时,求点O在此过程中运动的路径长.(参考数据:sin50°≈0.77.cos50°≈0.64,tan50°≈1.19,π取3.14)
7.如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得到线段FG,连接EF, CG.(1)求证:EF // CG;
(2)求点C,点A在旋转过程中形成的
AC,AG与线段CG所围成的阴影部分的面积.
╮
╮
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
3.9 弧长及扇形的面积
情景导入
如图,某传送带的一个转动伦的半径为10cm.
(1)转动轮转一周,传送带上的物品A被传送多少厘米?
(2)转动轮转1°,传送带上的物品A被传送多少厘米?
(3)转动轮转n°,传送带上的物品A被传送多少厘米?
n°圆心角所对的弧长
合作探究
∵圆的周长是C=2πR它所对的中心角是360?
那么1°的圆心角所对弧长
例1 制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度l.(单位:mm,精确到1mm)
解:由弧长公式,可得AB的长
因此所要求的展直长度l=2×700+1570=2970(mm).
答:管道的展直长度为2970mm.
700mm
700mm
R=900mm
(
100 °
A
C
B
D
O
(
练习.如图,四边形ABCD是⊙O的内接四边形,☉O的半径为4,∠B=135°,则弧AC的长为_________.
2π
上面图形BAC是扇形吗?
.o
A
B
C
r
B
A
C
.
B
C
A
√
×
×
半径为R的圆的面积S=πR2 ,由于圆所对的中心角是360?,
那么中心角是n?的扇形的面积应是
问题:扇形的弧长公式与面积公式有联系吗?
想一想 扇形的面积公式与什么公式类似?
A
B
O
O
例1 如图,已知圆O的半径12cm,圆心角∠AOB=120o,求AB的长(结果精确到0.1cm2)和扇形OAB的面积(结果精确到0.1cm2).
(
解:AB=
(
为什么这二种解法会产生答案不同,主要是弧长计算时已经是约数了,如果要用第二种解法,弧长要么写成分数,要么多精确一位。
例2 如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm)
O .
B
A
C
解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交AB于点C,连接AC.
∵ OC=0.6, DC=0.3,
∴ OD=OC- DC=0.3,
∴ OD=DC.
又 AD ⊥DC,
∴AD是线段OC的垂直平分线,
∴AC=AO=OC.
从而 ∠AOD=60?, ∠AOB=120?.
有水部分的面积:
S=S扇形OAB - S ΔOAB
┑
D
例2变式.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.
O
A
B
D
C
E
O
O
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
1. (2018·广东)如图,矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为 .(结果保留π)
割补思想
S阴=S?BCD-(S正方形OECD-S扇形OED)
=π
2.将△ABC绕点B逆时针旋转到△A'BC',使A、B、C'在同一直线上,∠BCA=90°,∠BAC=30°,AB =4 cm,则图2中阴影部分面积为__________cm2
S阴=S△A′BC′+S扇形A′BA-
S扇形BCC′-S△ABC=S扇形A′BA-
S扇形BCC′=4π
弧长
扇形
阴影部分面积
求法:整体思想
弓形
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
本课小结
课后作业
1.如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中弧CD、弧DE、弧EF的圆心依次是A、B、C,如果AB=1,求曲线CDEF的长.
解析:连接OB、OC,
∵AB是⊙O的切线,∴AB⊥BO.
∵∠A=30°,∴∠AOB=60°.
∵BC∥AO,∴∠OBC=∠AOB=60°.
在等腰△OBC中,
∠BOC=180°-2∠OBC=180°-2×60°=60°.
∴BC的长为 =2π(cm).
故答案为2π.
2.如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥AO.若∠A=30°,则劣弧BC的长为________cm.
︵
︵
2π
3.(淮安中考)如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点. (1)试判断直线DE与⊙O的位置关系,并说明理由; (2)若⊙O的半径为2,∠B=50°,AC=4.8,求图中阴影部分的面积.
∵点E是AC的中点,O点为AB的中点,∴OE∥BC,∴∠1=∠B,∠2=∠3,∵OB=OD,∴∠B=∠3,∴∠1=∠2,AO=DO,OE=OE(∠1=∠2),∴△AOE≌△DOE,∴∠ODE=∠OAE=90°,∴OD⊥DE,∴DE为⊙O的切线;
解:(1)直线DE与⊙O相切.
理由如下:连接OE、OD,如图,
∵AC是⊙O的切线,∴AB⊥AC,∴∠OAC=90°,
3.(淮安中考)如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点. (1)试判断直线DE与⊙O的位置关系,并说明理由; (2)若⊙O的半径为2,∠B=50°,AC=4.8,求图中阴影部分的面积.
4.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF. (1)求证:OF∥BC; (2)求证:△AFO≌△CEB; (3)若EB=5cm,CD=10 cm,设OE=x,求x的值及阴影部分的面积.
(1)证明:∵AB是⊙O直径,∴∠ACB=90°,
又OF⊥AC,∴CB∥OF;
(2)证明:在△CEB和△AFO中,BE=OF,
∠B=∠AOF,∠CEB=∠AFO=90°,∴△AFO≌△CEB;
4.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF. (1)求证:OF∥BC; (2)求证:△AFO≌△CEB; (3)若EB=5cm,CD=10 cm,设OE=x,求x的值及阴影部分的面积.
5. (2018·河南)如图,在△ABC中,∠ACB=90°,AC=BC=2.将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′,其中点B的运动路径为(BB′),则图中阴影部分的面积为 .
︵
6. (2018·江西)图①是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框上,通过推动左侧活页门开关.图②是其俯视简化示意图,已知轨道AB=120 cm,两扇活页门的宽OC=OB=60 m,点B固定,当点C在AB上左右运动时,OC与OB的长度不变.(所有的结果保留小数点后一位)(1)若∠OBC=50°,求AC的长;
(2)当点C从点A向右运动60 cm时,求点O在此过程中运动的路径长.(参考数据:sin50°≈0.77.cos50°≈0.64,tan50°≈1.19,π取3.14)
7.如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得到线段FG,连接EF, CG.(1)求证:EF // CG;
(2)求点C,点A在旋转过程中形成的
AC,AG与线段CG所围成的阴影部分的面积.
╮
╮
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
