1.6等腰梯形的轴对称性（2）

等腰梯形的轴对称性（二）学案
学习目标：
记住等腰梯形的判定方法。
学习重点与难点：
重点：等腰梯形的性质的应用。
难点：等腰梯形性质的探究。
学习过程：
知识梳理
在同一底上的两个角相等的题型是等腰梯形。
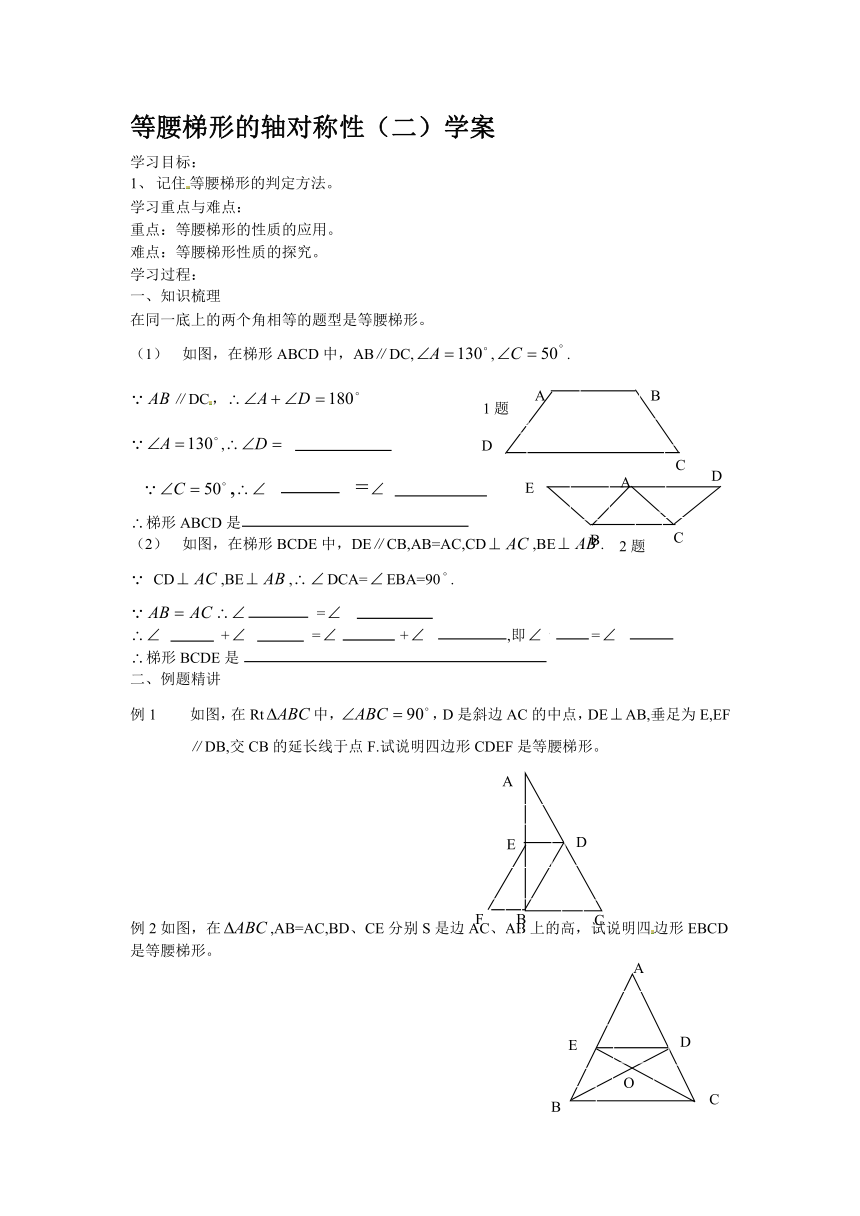
如图，在梯形ABCD中，AB∥DC,,.
∥DC，
,
, =
梯形ABCD是
如图，在梯形BCDE中，DE∥CB,AB=AC,CD,BE.
CD,BE,DCA=EBA=90.
=
+ = + ,即 =
梯形BCDE是
例题精讲
如图，在Rt中，，D是斜边AC的中点，DEAB,垂足为E,EF∥DB,交CB的延长线于点F.试说明四边形CDEF是等腰梯形。
例2如图，在,AB=AC,BD、CE分别S是边AC、AB上的高，试说明四边形EBCD是等腰梯形。
尝试练习
一个四边形的四个内角的度数之比是2：2：1：1，则此四边形的形状为
下列说法正确的是 （ ）
A 一组对边平行，另一组对边相等的四边形是等腰梯形
B 有一组对角互补的梯形是等腰梯形
C有一组对角相等的梯形是等腰梯形
D两组对角分别相等的梯形是等腰梯形
3、如图，9个点在平面上形成3×3的方阵，以这些点为顶点的等腰梯形有（ ）
A 0个 B 2个 C 4个 D 8 个
4、在梯形ABCD中，AD∥BC,E、F分别是AD、BC的中点，且EF则梯形ABCD是等腰梯形吗？为什么？
1题
A
B
D
A
D
C
E
2题
C
B
A
E
D
B
F
C
A
E
D
O
C
B
A
3题
E
D
A
C
B
F