2.7勾股定理的应用（2）

2.7勾股定理的应用（2）学案
一 学习目标
1 利用直角三角形的一些性质与勾股定理相结合解决一些实际问题。
2 在解决实际问题中体会数形结合的思想，感受数学在实际生活中的重要性。
二 预习交流
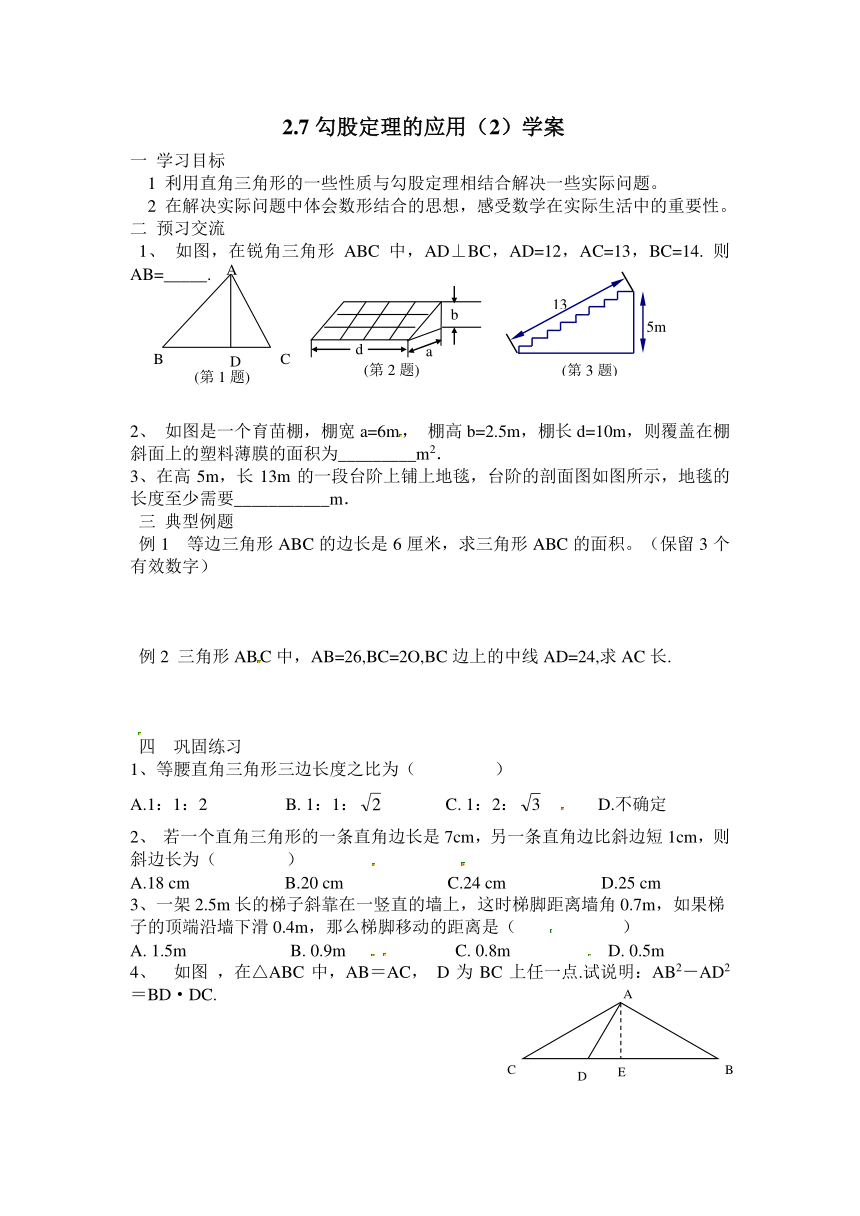
1、 如图，在锐角三角形ABC中，AD⊥BC，AD=12，AC=13，BC=14. 则AB=_____.
2、 如图是一个育苗棚，棚宽a=6m， 棚高b=2.5m，棚长d=10m，则覆盖在棚斜面上的塑料薄膜的面积为_________m2．
3、在高5m，长13m的一段台阶上铺上地毯，台阶的剖面图如图所示，地毯的长度至少需要___________m．
三 典型例题
例1 等边三角形ABC的边长是6厘米，求三角形ABC的面积。（保留3个有效数字）
例2 三角形ABC中，AB=26,BC=2O,BC边上的中线AD=24,求AC长.
四 巩固练习
1、等腰直角三角形三边长度之比为（ ）
A.1：1：2 B. 1：1： C. 1：2： D.不确定
2、 若一个直角三角形的一条直角边长是7cm，另一条直角边比斜边短1cm，则斜边长为（ ）
A.18 cm B.20 cm C.24 cm D.25 cm
3、一架2.5m长的梯子斜靠在一竖直的墙上，这时梯脚距离墙角0.7m，如果梯子的顶端沿墙下滑0.4m，那么梯脚移动的距离是（ ）
A. 1.5m B. 0.9m 　 C. 0.8m 　 D. 0.5m
4、　如图 ，在△ABC中，AB＝AC， D为BC上任一点.试说明：AB2－AD2＝BD·DC.
5、如图 ，一块草坪的形状为四边形ABCD，其中∠B=90 ，AB=3m，BC=4m，CD
=12m，AD=13m，求这块草坪的面积。
6、如图，分别以直角三角形的三边为边长向外作正方形，边长分别a、b、c（c表示斜边）然后分别以三个正方形的中心为圆心、正方形边长的一半为半径作圆，三个圆的面积分别记为S1、S2、S3，试探索三个圆的面积之间的关系.
7、甲
、乙两人在沙漠进行探险，某日早晨8∶00甲先出发，他以6千米/时速度向东南方向行走，1小时后乙出发，他以5千米/时速度向西南方向行走，上午10∶00时，甲、乙两人相距多远？
8、要登上9m高的建筑物，为了安全需要，需使梯子固定在一个高1m的固定架上，并且底端离建筑物6m，梯子至多需要多长？
A
B
C
D
(第1题)
b
d
a
(第2题)
13m
5m
(第3题)
E
A
D
B
C
A
B
C
D