2020-2021学年青岛新版八年级下册数学《第6章 平行四边形》单元测试卷(word解析版)
文档属性
| 名称 | 2020-2021学年青岛新版八年级下册数学《第6章 平行四边形》单元测试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 00:00:00 | ||
图片预览



文档简介
2020-2021学年青岛新版八年级下册数学《第6章
平行四边形》单元测试卷
一.选择题
1.如图所示,在平行四边形ABCD中,对角线AC、BD交于O点,过O点作直线交AD于E,交BC于F,图中能够全等的三角形共有( )
A.2对
B.4对
C.6对
D.8对
2.如图所示,在?ABCD中,EF∥GH∥AB,MN∥BC,则图中的平行四边形的个数为( )
A.12个
B.16个
C.14个
D.18个
3.已知菱形的周长为16CM,一条对角线长为4CM,则菱形的4个角分别为( )
A.30°、150°、30°、150°
B.45°、135°、45°、135°
C.60°、120°、60°、120°
D.以上都不对
4.四边相等的四边形一定是( )
A.矩形
B.菱形
C.正方形
D.无法判定
5.已知四边形ABCD中,AC⊥BD,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH是( )
A.菱形
B.矩形
C.正方形
D.梯形
6.能判别一个四边形是正方形的条件是( )
A.对角线相等,对边平行且相等
B.一组对边平行,一组对角相等
C.对角线互相垂直平分且相等
D.一组邻边相等,对角线互相平分
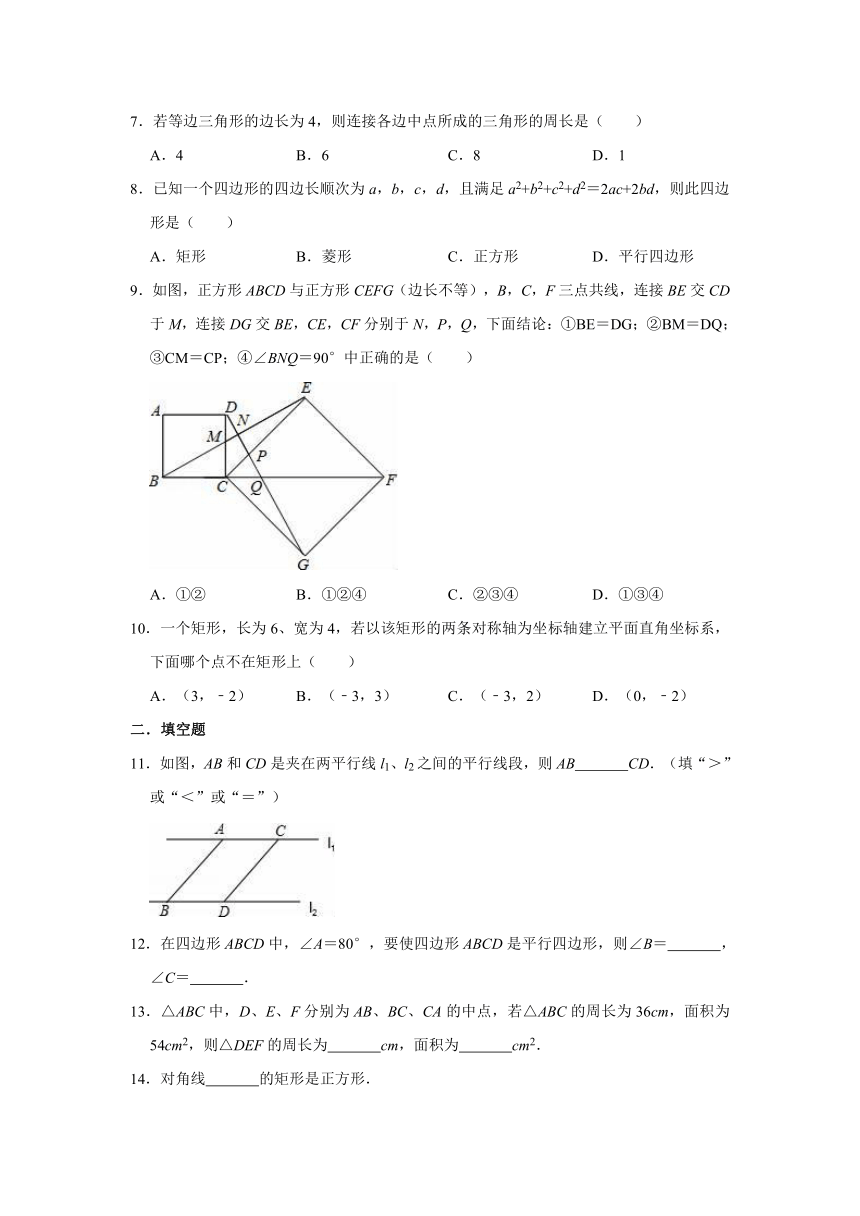
7.若等边三角形的边长为4,则连接各边中点所成的三角形的周长是( )
A.4
B.6
C.8
D.1
8.已知一个四边形的四边长顺次为a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则此四边形是( )
A.矩形
B.菱形
C.正方形
D.平行四边形
9.如图,正方形ABCD与正方形CEFG(边长不等),B,C,F三点共线,连接BE交CD于M,连接DG交BE,CE,CF分别于N,P,Q,下面结论:①BE=DG;②BM=DQ;③CM=CP;④∠BNQ=90°中正确的是( )
A.①②
B.①②④
C.②③④
D.①③④
10.一个矩形,长为6、宽为4,若以该矩形的两条对称轴为坐标轴建立平面直角坐标系,下面哪个点不在矩形上( )
A.(3,﹣2)
B.(﹣3,3)
C.(﹣3,2)
D.(0,﹣2)
二.填空题
11.如图,AB和CD是夹在两平行线l1、l2之间的平行线段,则AB
CD.(填“>”或“<”或“=”)
12.在四边形ABCD中,∠A=80°,要使四边形ABCD是平行四边形,则∠B=
,∠C=
.
13.△ABC中,D、E、F分别为AB、BC、CA的中点,若△ABC的周长为36cm,面积为54cm2,则△DEF的周长为
cm,面积为
cm2.
14.对角线
的矩形是正方形.
15.如图,P是正方形ABCD内任意一点,△APD与△BPC的面积之和为8cm2,则AB=
cm.
16.任意一个平行四边形,当它的一个锐角增大到
度时,就变成了矩形;当它的一组邻边变到
时,就变成了菱形.
17.如图,矩形ABCD的长为8cm,宽为6cm,O是对称中心,则图中阴影部分的面积是
.
18.已知在菱形ABCD中,∠ABC=60°,对角线AC=2,则边长为
.
19.如图,已知四边形ABCD是一个平行四边形,则只须补充条件
,就可以判定它是一个菱形.
20.在?ABCD中,AD=BD,BE是AD边上的高,∠EBD=28°,则∠A的度数为
.
三.解答题
21.如图,已知在平行四边形ABCD中,E,F为边AD,BC上的点,且AE=CF,连接AF,EC,BE,DF交于M,N,试判断MF与NE的关系,并证明你的结论.
22.在直角坐标系中以A(﹣0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,并写出第四个顶点D的坐标.
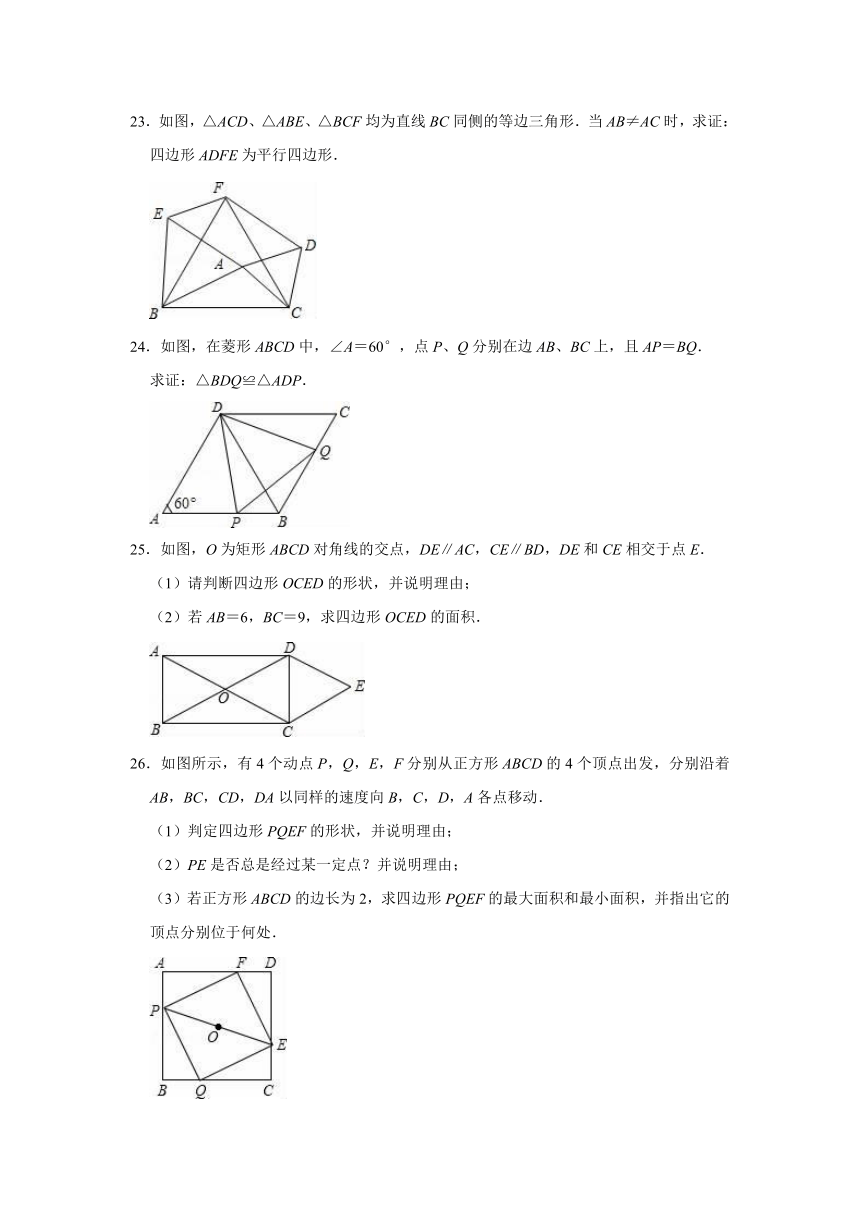
23.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.当AB≠AC时,求证:四边形ADFE为平行四边形.
24.如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.
求证:△BDQ≌△ADP.
25.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD,DE和CE相交于点E.
(1)请判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=9,求四边形OCED的面积.
26.如图所示,有4个动点P,Q,E,F分别从正方形ABCD的4个顶点出发,分别沿着AB,BC,CD,DA以同样的速度向B,C,D,A各点移动.
(1)判定四边形PQEF的形状,并说明理由;
(2)PE是否总是经过某一定点?并说明理由;
(3)若正方形ABCD的边长为2,求四边形PQEF的最大面积和最小面积,并指出它的顶点分别位于何处.
27.在△ABC中,AB=2AC,AF=AB,D、E分别为AB、BC的中点,EF与CA的延长线交于点G,求证:AF=AG.
参考答案与试题解析
一.选择题
1.解:由平行四边形的中心对称性,全等三角形有:△AOB≌△COD,△AOD≌△COB,△AOE≌△COF,△DOE≌△BOF,△ABD≌△CDB,△ABC≌△CDA共6对.
故选:C.
2.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边形AEOM、AEFB、AMND、CNOF、CNMB、CDEF、DNOE、BMOF、AGPM、GPND、MPHB、HPCN、OEGP、OPHF、EGHF、GHCD、AGHB和ABCD都是平行四边形,共18个.
故选:D.
3.解:如图
由菱形周长可得菱形变长为4,即AB=4,
又一条对角线为4,即BD=4,
∴OB=2=AB,
∴在Rt△AOB中,∠OAB=30°,
∴∠DAB=60°
∴∠ADC=120°
故选:C.
4.解:根据菱形的判定:四边相等的四边形是菱形.
故选:B.
5.解:如图,
依题意四边形ABCD,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点,
根据矩形的判定(矩形的对角线相等且相互平分)可得四边形EFGH是矩形.
故选:B.
6.解:A中对边平行且相等,可得其为平行四边形,又对角线相等,可得其为矩形,A错;
B中只能判定是平行四边形,B错;
C中对角线平分且相等是平行四边形,再加上对角线互相垂直,即为正方形,C对;
D中是菱形,D错.
故选:C.
7.解:∵原等边三角形的边长=4,
∴原等边三角形的周长=3×4=12,
∴中点三角形的周长=×12=6.
故选:B.
8.解:根据a2+b2+c2+d2=2ac+2bd,整理得:(a﹣c)2+(b﹣d)2=0.那么a=c,b=d.所以此四边形是平行四边形.
故选:D.
9.解:在正方形ABCD与正方形CEFG中,
BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCD+∠DCE=∠ECG+∠DCE,
即∠BCE=∠DCG,
在△BCE和△DCG中,
,
∴△BCE≌△DCG(SAS),
∴BE=DG,∠CBE=∠CDG,故①正确;
在△BCM和△DCQ中,
,
∴△BCM≌△DCQ(ASA),
∴BM=DQ,CM=CQ,故②正确;
在Rt△CPG中,∠CGP+∠CPG=90°,
在Rt△CDQ中,∠CDQ+∠CQD=90°,
∵正方形ABCD与正方形CEFG的边长不等,
∴∠CDQ≠∠CGP,
∴∠CQD≠CPG,
∴CQ≠CP,
∴CM≠CP,故③错误;
∵∠CBE+∠BMC=90°,∠CBE=∠CDG,∠BMC=∠DMN(对顶角相等),
∴∠CDG+∠DMN=90°,
∴∠DNM=90°,
∴∠BNQ=180°﹣∠DNM=180°﹣90°=90°,故④正确,
综上所述,正确的结论有①②④.
故选:B.
10.解:建立如图所示的直角坐标系,
矩形的四个顶点坐标是(﹣3,2),(﹣3,﹣2),(3,2),(3,﹣2);
或(﹣2,3),(﹣2,﹣3),(2,3),(2,﹣3),
故选:B.
二.填空题
11.解:∵l1∥l2,AB∥CD,
∴ABCD是平行四边形,
∴AB=CD
故答案为:=.
12.解:∵∠A=80°,∠B=100°,
∴∠A+∠B=180°,
∴AD∥BC,
∵∠B=100°,∠C=80°,
∴∠B+∠C=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形,
故答案为:100°;80°.
13.解:∵在△ABC中,点D、E、F分别是AB、BC、CA的中点,
∴===,
∴△DEF∽△CAB,
∴=,=()2=,
∵△ABC的周长为36cm,面积为54cm2,
∴△DEF的周长=×36=18cm,△DEF的面积=×54=13.5cm2.
故答案为:18,13.5.
14.解:对角线互相垂直的矩形是正方形.故答案为:互相垂直.
15.解:如图,过点P作EF∥AB,MN∥BC,则正方形ABCD被分成四个小矩形,
所以,S△APE=S△APM,S△BPM=S△BPF,S△CPF=S△CPN,S△DPE=S△DPN,
∴S△APD+S△BPC=S正方形ABCD,
∵△APD与△BPC的面积之和为8cm2,
∴正方形ABCD的面积为16cm2,
∴AB=4cm.
故答案为:4.
16.解:因为平行四边形两组对边分别平行且相等,所以当一个锐角增加为90°时,四个角都是90°,可得其为矩形;
当平行四边形的一组邻边相等时,四条边都相等,所以四边形是菱形.
故答案为:90,相等.
17.解:∵四边形ABCD是矩形,O是对称中心,
∴BF=DE,
∴S阴影=(BF+AE)?AB=(DE+AE)?AB=AD?AB,
∵矩形ABCD的长为8cm,宽为6cm,
∴S阴影=AD?AB=×8×6=24cm2.
故答案为:24cm2.
18.解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=2.
即边长为2.
故答案为:2.
19.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
20.解:根据平行四边形的性质和题意画出图形,分2种情况:①如图1所示
∵BE是AD边上的高,∠EBD=28°,
∴∠BDE=90°﹣28°=62°,
∵AD=BD,
∴∠A=∠ABD=(180°﹣62°)=59°;
②如图2所示:同①得:∠BDE=62°,
∵AD=BD,
∴∠A=∠ABD,
∴∠A=62°÷2=31°;
上所述:∠A的度数为59°或31°,
故答案为:59°或31°.
三.解答题
21.解:MF=NE,且MF∥NE.理由如下:
∵四边形ABCD是平行四边形,则AD∥BC.
∵AE=CF,
∴DEBF,
∴四边形BEDF是平行四边形,
∴BE∥DF,即ME∥FN.
∵AECF,
∴四边形AECF是平行四边形,
∴MF∥EN,
∴四边形MENF是平行四边形,
∴MF=NE,且MF∥NE.
22.解:如图,根据平行四边形的两组对边分别平行,可得D点有三种情况,
所以D点坐标为(2.5,1)或(﹣2.5,1)或(1.5,﹣1).
23.证明:
∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.
∴∠FBE=∠CBA,
在△FBE和△CBA中,
,
∴△FBE≌△CBA(SAS).
∴EF=AC.
又∵△ADC为等边三角形,
∴CD=AD=AC.
∴EF=AD.
同理可得AE=DF.
∴四边形AEFD是平行四边形.
24.证明:∵四边形ABCD是菱形,且∠A=60°,
∴AD=AB=BC=CD,∠C=∠A=60°,
∴△ABD和△BDC是等边三角形,
∴∠DBQ=∠A=60°,AD=DB,
在△BDQ和△ADP中,
,
∴△BDQ≌△ADP(SAS).
25.解:(1)四边形OCED是菱形,理由如下:
∵DE∥AC,CE∥BD,
∵四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AO=OC=BO=OD.
∴四边形OCED是菱形;
(2)∵四边形ABCD是矩形,AB=6,BC=9,
∴△OCD的面积=矩形ABCD的面积=×AB×BC=×6×9=,
∵四边形OCED是菱形,
∴四边形OCED的面积=2△OCD的面积=27.
26.解:(1)在正方形ABCD中,AP=BQ=CE=DF,AB=BC=CD=DA,
∴BP=QC=ED=FA.
又∵∠BAD=∠B=∠BCD=∠D=90°,
∴△AFP≌△BPQ≌△CQE≌△DEF.
∴FP=PQ=QE=EF,∠APF=∠PQB.
∵∠FPQ=90°,
∴四边形PQEF为正方形;
(2)连接PE交AC于O,连接PC、AE,
∵AP平行且等于EC,
∴四边形APCE为平行四边形.
∴O为对角线AC的中点,
∴对角线PE总过AC的中点;
(3)正方形ABCD与正方形PQEF的对角线交点是重合的,
当OP⊥AB时,四边形PQEF面积最小,为原正方形面积的一半,即为×2×2=2;
当P与顶点B重合时,面积最大,其最大面积等于正方形ABCD的面积即为:2×2=4.
27.证明:取AC的中点M,连接EM,
∵E,M,分别是BC,AC的中点,
∴EM是△ABC的中位线,
又∵EM=AB,AF=AB,
∴AF=EM,
又∵EM∥AB,
∴==,即AG=AM=AC,
∵AC=AB,
∴AG=AB,
∵AF=AB,
∴AG=AF.
平行四边形》单元测试卷
一.选择题
1.如图所示,在平行四边形ABCD中,对角线AC、BD交于O点,过O点作直线交AD于E,交BC于F,图中能够全等的三角形共有( )
A.2对
B.4对
C.6对
D.8对
2.如图所示,在?ABCD中,EF∥GH∥AB,MN∥BC,则图中的平行四边形的个数为( )
A.12个
B.16个
C.14个
D.18个
3.已知菱形的周长为16CM,一条对角线长为4CM,则菱形的4个角分别为( )
A.30°、150°、30°、150°
B.45°、135°、45°、135°
C.60°、120°、60°、120°
D.以上都不对
4.四边相等的四边形一定是( )
A.矩形
B.菱形
C.正方形
D.无法判定
5.已知四边形ABCD中,AC⊥BD,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH是( )
A.菱形
B.矩形
C.正方形
D.梯形
6.能判别一个四边形是正方形的条件是( )
A.对角线相等,对边平行且相等
B.一组对边平行,一组对角相等
C.对角线互相垂直平分且相等
D.一组邻边相等,对角线互相平分
7.若等边三角形的边长为4,则连接各边中点所成的三角形的周长是( )
A.4
B.6
C.8
D.1
8.已知一个四边形的四边长顺次为a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则此四边形是( )
A.矩形
B.菱形
C.正方形
D.平行四边形
9.如图,正方形ABCD与正方形CEFG(边长不等),B,C,F三点共线,连接BE交CD于M,连接DG交BE,CE,CF分别于N,P,Q,下面结论:①BE=DG;②BM=DQ;③CM=CP;④∠BNQ=90°中正确的是( )
A.①②
B.①②④
C.②③④
D.①③④
10.一个矩形,长为6、宽为4,若以该矩形的两条对称轴为坐标轴建立平面直角坐标系,下面哪个点不在矩形上( )
A.(3,﹣2)
B.(﹣3,3)
C.(﹣3,2)
D.(0,﹣2)
二.填空题
11.如图,AB和CD是夹在两平行线l1、l2之间的平行线段,则AB
CD.(填“>”或“<”或“=”)
12.在四边形ABCD中,∠A=80°,要使四边形ABCD是平行四边形,则∠B=
,∠C=
.
13.△ABC中,D、E、F分别为AB、BC、CA的中点,若△ABC的周长为36cm,面积为54cm2,则△DEF的周长为
cm,面积为
cm2.
14.对角线
的矩形是正方形.
15.如图,P是正方形ABCD内任意一点,△APD与△BPC的面积之和为8cm2,则AB=
cm.
16.任意一个平行四边形,当它的一个锐角增大到
度时,就变成了矩形;当它的一组邻边变到
时,就变成了菱形.
17.如图,矩形ABCD的长为8cm,宽为6cm,O是对称中心,则图中阴影部分的面积是
.
18.已知在菱形ABCD中,∠ABC=60°,对角线AC=2,则边长为
.
19.如图,已知四边形ABCD是一个平行四边形,则只须补充条件
,就可以判定它是一个菱形.
20.在?ABCD中,AD=BD,BE是AD边上的高,∠EBD=28°,则∠A的度数为
.
三.解答题
21.如图,已知在平行四边形ABCD中,E,F为边AD,BC上的点,且AE=CF,连接AF,EC,BE,DF交于M,N,试判断MF与NE的关系,并证明你的结论.
22.在直角坐标系中以A(﹣0.5,0),B(2,0),C(0,1)三点为顶点画平行四边形,并写出第四个顶点D的坐标.
23.如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.当AB≠AC时,求证:四边形ADFE为平行四边形.
24.如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.
求证:△BDQ≌△ADP.
25.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD,DE和CE相交于点E.
(1)请判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=9,求四边形OCED的面积.
26.如图所示,有4个动点P,Q,E,F分别从正方形ABCD的4个顶点出发,分别沿着AB,BC,CD,DA以同样的速度向B,C,D,A各点移动.
(1)判定四边形PQEF的形状,并说明理由;
(2)PE是否总是经过某一定点?并说明理由;
(3)若正方形ABCD的边长为2,求四边形PQEF的最大面积和最小面积,并指出它的顶点分别位于何处.
27.在△ABC中,AB=2AC,AF=AB,D、E分别为AB、BC的中点,EF与CA的延长线交于点G,求证:AF=AG.
参考答案与试题解析
一.选择题
1.解:由平行四边形的中心对称性,全等三角形有:△AOB≌△COD,△AOD≌△COB,△AOE≌△COF,△DOE≌△BOF,△ABD≌△CDB,△ABC≌△CDA共6对.
故选:C.
2.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边形AEOM、AEFB、AMND、CNOF、CNMB、CDEF、DNOE、BMOF、AGPM、GPND、MPHB、HPCN、OEGP、OPHF、EGHF、GHCD、AGHB和ABCD都是平行四边形,共18个.
故选:D.
3.解:如图
由菱形周长可得菱形变长为4,即AB=4,
又一条对角线为4,即BD=4,
∴OB=2=AB,
∴在Rt△AOB中,∠OAB=30°,
∴∠DAB=60°
∴∠ADC=120°
故选:C.
4.解:根据菱形的判定:四边相等的四边形是菱形.
故选:B.
5.解:如图,
依题意四边形ABCD,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点,
根据矩形的判定(矩形的对角线相等且相互平分)可得四边形EFGH是矩形.
故选:B.
6.解:A中对边平行且相等,可得其为平行四边形,又对角线相等,可得其为矩形,A错;
B中只能判定是平行四边形,B错;
C中对角线平分且相等是平行四边形,再加上对角线互相垂直,即为正方形,C对;
D中是菱形,D错.
故选:C.
7.解:∵原等边三角形的边长=4,
∴原等边三角形的周长=3×4=12,
∴中点三角形的周长=×12=6.
故选:B.
8.解:根据a2+b2+c2+d2=2ac+2bd,整理得:(a﹣c)2+(b﹣d)2=0.那么a=c,b=d.所以此四边形是平行四边形.
故选:D.
9.解:在正方形ABCD与正方形CEFG中,
BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCD+∠DCE=∠ECG+∠DCE,
即∠BCE=∠DCG,
在△BCE和△DCG中,
,
∴△BCE≌△DCG(SAS),
∴BE=DG,∠CBE=∠CDG,故①正确;
在△BCM和△DCQ中,
,
∴△BCM≌△DCQ(ASA),
∴BM=DQ,CM=CQ,故②正确;
在Rt△CPG中,∠CGP+∠CPG=90°,
在Rt△CDQ中,∠CDQ+∠CQD=90°,
∵正方形ABCD与正方形CEFG的边长不等,
∴∠CDQ≠∠CGP,
∴∠CQD≠CPG,
∴CQ≠CP,
∴CM≠CP,故③错误;
∵∠CBE+∠BMC=90°,∠CBE=∠CDG,∠BMC=∠DMN(对顶角相等),
∴∠CDG+∠DMN=90°,
∴∠DNM=90°,
∴∠BNQ=180°﹣∠DNM=180°﹣90°=90°,故④正确,
综上所述,正确的结论有①②④.
故选:B.
10.解:建立如图所示的直角坐标系,
矩形的四个顶点坐标是(﹣3,2),(﹣3,﹣2),(3,2),(3,﹣2);
或(﹣2,3),(﹣2,﹣3),(2,3),(2,﹣3),
故选:B.
二.填空题
11.解:∵l1∥l2,AB∥CD,
∴ABCD是平行四边形,
∴AB=CD
故答案为:=.
12.解:∵∠A=80°,∠B=100°,
∴∠A+∠B=180°,
∴AD∥BC,
∵∠B=100°,∠C=80°,
∴∠B+∠C=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形,
故答案为:100°;80°.
13.解:∵在△ABC中,点D、E、F分别是AB、BC、CA的中点,
∴===,
∴△DEF∽△CAB,
∴=,=()2=,
∵△ABC的周长为36cm,面积为54cm2,
∴△DEF的周长=×36=18cm,△DEF的面积=×54=13.5cm2.
故答案为:18,13.5.
14.解:对角线互相垂直的矩形是正方形.故答案为:互相垂直.
15.解:如图,过点P作EF∥AB,MN∥BC,则正方形ABCD被分成四个小矩形,
所以,S△APE=S△APM,S△BPM=S△BPF,S△CPF=S△CPN,S△DPE=S△DPN,
∴S△APD+S△BPC=S正方形ABCD,
∵△APD与△BPC的面积之和为8cm2,
∴正方形ABCD的面积为16cm2,
∴AB=4cm.
故答案为:4.
16.解:因为平行四边形两组对边分别平行且相等,所以当一个锐角增加为90°时,四个角都是90°,可得其为矩形;
当平行四边形的一组邻边相等时,四条边都相等,所以四边形是菱形.
故答案为:90,相等.
17.解:∵四边形ABCD是矩形,O是对称中心,
∴BF=DE,
∴S阴影=(BF+AE)?AB=(DE+AE)?AB=AD?AB,
∵矩形ABCD的长为8cm,宽为6cm,
∴S阴影=AD?AB=×8×6=24cm2.
故答案为:24cm2.
18.解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=2.
即边长为2.
故答案为:2.
19.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
20.解:根据平行四边形的性质和题意画出图形,分2种情况:①如图1所示
∵BE是AD边上的高,∠EBD=28°,
∴∠BDE=90°﹣28°=62°,
∵AD=BD,
∴∠A=∠ABD=(180°﹣62°)=59°;
②如图2所示:同①得:∠BDE=62°,
∵AD=BD,
∴∠A=∠ABD,
∴∠A=62°÷2=31°;
上所述:∠A的度数为59°或31°,
故答案为:59°或31°.
三.解答题
21.解:MF=NE,且MF∥NE.理由如下:
∵四边形ABCD是平行四边形,则AD∥BC.
∵AE=CF,
∴DEBF,
∴四边形BEDF是平行四边形,
∴BE∥DF,即ME∥FN.
∵AECF,
∴四边形AECF是平行四边形,
∴MF∥EN,
∴四边形MENF是平行四边形,
∴MF=NE,且MF∥NE.
22.解:如图,根据平行四边形的两组对边分别平行,可得D点有三种情况,
所以D点坐标为(2.5,1)或(﹣2.5,1)或(1.5,﹣1).
23.证明:
∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.
∴∠FBE=∠CBA,
在△FBE和△CBA中,
,
∴△FBE≌△CBA(SAS).
∴EF=AC.
又∵△ADC为等边三角形,
∴CD=AD=AC.
∴EF=AD.
同理可得AE=DF.
∴四边形AEFD是平行四边形.
24.证明:∵四边形ABCD是菱形,且∠A=60°,
∴AD=AB=BC=CD,∠C=∠A=60°,
∴△ABD和△BDC是等边三角形,
∴∠DBQ=∠A=60°,AD=DB,
在△BDQ和△ADP中,
,
∴△BDQ≌△ADP(SAS).
25.解:(1)四边形OCED是菱形,理由如下:
∵DE∥AC,CE∥BD,
∵四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AO=OC=BO=OD.
∴四边形OCED是菱形;
(2)∵四边形ABCD是矩形,AB=6,BC=9,
∴△OCD的面积=矩形ABCD的面积=×AB×BC=×6×9=,
∵四边形OCED是菱形,
∴四边形OCED的面积=2△OCD的面积=27.
26.解:(1)在正方形ABCD中,AP=BQ=CE=DF,AB=BC=CD=DA,
∴BP=QC=ED=FA.
又∵∠BAD=∠B=∠BCD=∠D=90°,
∴△AFP≌△BPQ≌△CQE≌△DEF.
∴FP=PQ=QE=EF,∠APF=∠PQB.
∵∠FPQ=90°,
∴四边形PQEF为正方形;
(2)连接PE交AC于O,连接PC、AE,
∵AP平行且等于EC,
∴四边形APCE为平行四边形.
∴O为对角线AC的中点,
∴对角线PE总过AC的中点;
(3)正方形ABCD与正方形PQEF的对角线交点是重合的,
当OP⊥AB时,四边形PQEF面积最小,为原正方形面积的一半,即为×2×2=2;
当P与顶点B重合时,面积最大,其最大面积等于正方形ABCD的面积即为:2×2=4.
27.证明:取AC的中点M,连接EM,
∵E,M,分别是BC,AC的中点,
∴EM是△ABC的中位线,
又∵EM=AB,AF=AB,
∴AF=EM,
又∵EM∥AB,
∴==,即AG=AM=AC,
∵AC=AB,
∴AG=AB,
∵AF=AB,
∴AG=AF.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
