2020-2021学年人教版八年级物理下册课件-9.3 大气压强(30张)
文档属性
| 名称 | 2020-2021学年人教版八年级物理下册课件-9.3 大气压强(30张) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-01 19:57:12 | ||
图片预览










文档简介
第3节 大气压强
瓶吞气球
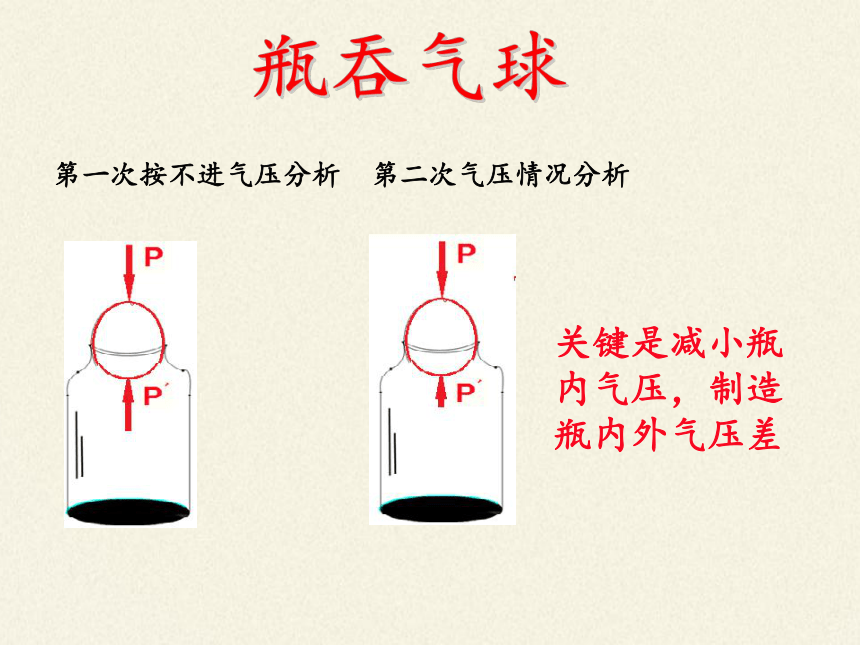
瓶吞气球
第一次按不进气压分析
第二次气压情况分析
关键是减小瓶内气压,制造瓶内外气压差
看也看不到,
摸也摸不着。
要想显示它,
制造气压差。
大气压
减小瓶内压,
实验器材
1组和4组实验要用到水槽中的水
一. 大气的方向:向各个方向都有压强
二.大气压产生的原因
大气受重力作用并具有流动性
第3节 大气压强
模拟马德堡半球实验
感受大气压大小
1654年5月8日,德国马德堡市的市民们看到了一件令人既惊奇又困惑的事情:他们的市长、发明抽气机的奥托·格里克,把两个直径35.5 cm的空心铜半球紧贴在一起,抽出球内的空气,然后用两队马,每队八匹马,向相反的方向拉两个半球,当这16匹马竭尽全力终于把两个半球拉开时,竟然像放炮一样发出了巨大的响声.这就是著名的马德堡半球实验.
马德堡半球实验
马德堡半球实验的意义
大气压究竟有多大?
我们想办法测出它的数值。
2.大气压很大
1.证明了大气压的存在
3.大气压不是无限大
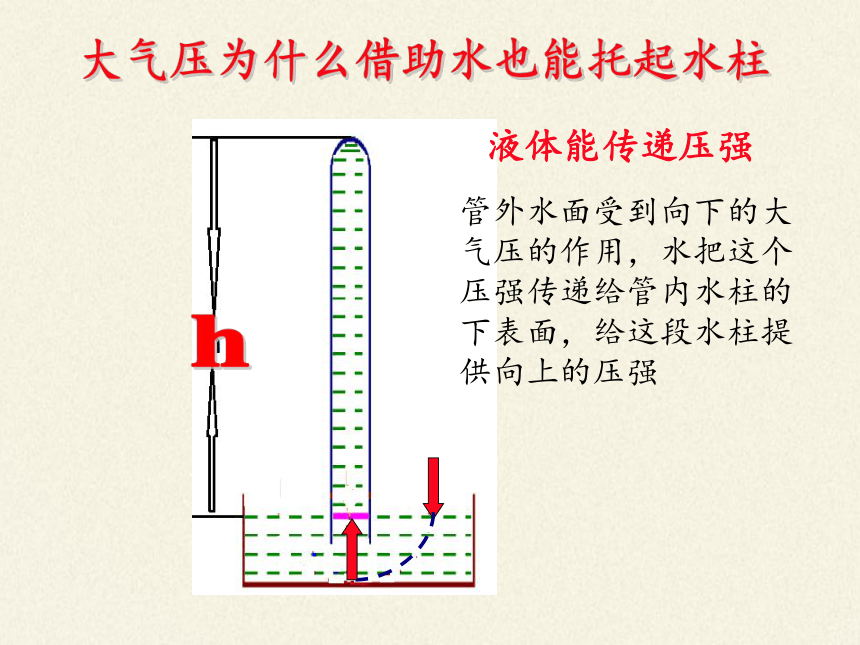
液体能传递压强
管外水面受到向下的大气压的作用,水把这个压强传递给管内水柱的下表面,给这段水柱提供向上的压强
大气压为什么借助水也能托起水柱
h
1.大气压托起的水柱可以无限高吗?为什么?
2.假设用无限长的玻璃管装满水,
倒立在水槽中,玻璃管中的水会怎样?
3.追问,一直下落吗?什么时候不再下落?
4.大气压究竟能托起多高的水柱?
理论探究
大气压能托起多高的水柱?
怎样计算出大气压的数值?
P大气=P水柱=ρ水gh
P大气= P液柱 =ρ液gh
物质
密度/(kg/m3)
物质
密度/(kg/m3)
水银
13.6×103
植物油
0.9×103
硫酸
1.8×103
煤油
0.8×103
海水
1.03×103
酒精
0.8×103
纯水
1.0×103
汽油
0.71×103
一些液体的密度(常温常压)
世界上最早精确测出大气压值的实验
二、大气压的测量
托里拆利实验
托里拆利
2. 760mm高水银柱产生的压强与大气压强
的关系是怎样的?
思考问题:
1. 管内水银柱不再下降是靠什么托住了它?
3.怎样计算出760mm高水银柱产生的压强
=13.6×103 kg/m3×9.8 N/kg×0.76 m
= ρ水银 gh
=1.013×105 Pa
p大气=p水银
标准大气压 p0= 1.013×105 Pa
粗略计算标准大气压可取为105 Pa
大气压有多大
1.管内水银柱的高度和是否将玻璃管提起、
玻璃管的粗细、倾斜有关吗?
(无关。 p大气= p水银= ρ水银gh )
2.如果玻璃管顶部破了会怎么样?
(玻璃管内水银下降至与水槽内水银液面相平)
讨论一:
1.如果在实验中细管内不小心混进了一些空气,
则测量值比真实值_____. (偏大,偏小,不变)
偏小
2.如果在实验中,外界大气压突然变小了,则玻璃
管中的水银柱高度将_____. (变大,变小,不变)
变小
讨论二:
一个油罐的表面积约为200m2,标准大气压取105 Pa,大气压对油罐的压力有多大?这么大的压力为什么没把油罐压瘪呢?抽去油罐里的空气会怎样?
想想议议1:
抽去油罐里的空气会怎样
我们人体每时每刻都承受着大气压作用,
为什么没有被压瘪呢?
想想议议2:
大气压的应用
观看视频
记下视频中介绍的大气压有哪些应用?
大气压的应用
究竟是吸上来的还是大气压上来的呢?
吸管吸饮料
没有大气压会怎样?
小结
一大气压产生的原因是
二 大气压方向特点
三 证实大气压存在的著名实验
马德堡半球实验
四 最早测出大气压值的实验
标准大气压的值是
粗略计算取
大气受到重力和具有流动性
向各个方向都有压强
托里拆利实验
1.013×105Pa
105 Pa
1.把装满水的试管浸入水中,口朝下如图那样抓住管底向上提,在管口离开水面前,试管露出水面的部分( )
A 是空的 B 有水,但不满
C 充满水 D 以上都有可能
C
2、在冬天,保温瓶未装满水,当瓶内温度下降时软木塞不易拔出,这主要是( )
A、塞子与瓶口间摩擦力太大
B、瓶口遇冷收缩
C、瓶内气压小于大气压
D、原先塞子塞的太紧
C
3、一同学在标准大气压下做托里拆利实验,测得管中水银面比槽里水银面高750毫米,他失败的原因( )
A管子粗了一些。
B管子长了一些
C管子不在竖直位置。
D管中漏入少量空气。
D
谢 谢
瓶吞气球
瓶吞气球
第一次按不进气压分析
第二次气压情况分析
关键是减小瓶内气压,制造瓶内外气压差
看也看不到,
摸也摸不着。
要想显示它,
制造气压差。
大气压
减小瓶内压,
实验器材
1组和4组实验要用到水槽中的水
一. 大气的方向:向各个方向都有压强
二.大气压产生的原因
大气受重力作用并具有流动性
第3节 大气压强
模拟马德堡半球实验
感受大气压大小
1654年5月8日,德国马德堡市的市民们看到了一件令人既惊奇又困惑的事情:他们的市长、发明抽气机的奥托·格里克,把两个直径35.5 cm的空心铜半球紧贴在一起,抽出球内的空气,然后用两队马,每队八匹马,向相反的方向拉两个半球,当这16匹马竭尽全力终于把两个半球拉开时,竟然像放炮一样发出了巨大的响声.这就是著名的马德堡半球实验.
马德堡半球实验
马德堡半球实验的意义
大气压究竟有多大?
我们想办法测出它的数值。
2.大气压很大
1.证明了大气压的存在
3.大气压不是无限大
液体能传递压强
管外水面受到向下的大气压的作用,水把这个压强传递给管内水柱的下表面,给这段水柱提供向上的压强
大气压为什么借助水也能托起水柱
h
1.大气压托起的水柱可以无限高吗?为什么?
2.假设用无限长的玻璃管装满水,
倒立在水槽中,玻璃管中的水会怎样?
3.追问,一直下落吗?什么时候不再下落?
4.大气压究竟能托起多高的水柱?
理论探究
大气压能托起多高的水柱?
怎样计算出大气压的数值?
P大气=P水柱=ρ水gh
P大气= P液柱 =ρ液gh
物质
密度/(kg/m3)
物质
密度/(kg/m3)
水银
13.6×103
植物油
0.9×103
硫酸
1.8×103
煤油
0.8×103
海水
1.03×103
酒精
0.8×103
纯水
1.0×103
汽油
0.71×103
一些液体的密度(常温常压)
世界上最早精确测出大气压值的实验
二、大气压的测量
托里拆利实验
托里拆利
2. 760mm高水银柱产生的压强与大气压强
的关系是怎样的?
思考问题:
1. 管内水银柱不再下降是靠什么托住了它?
3.怎样计算出760mm高水银柱产生的压强
=13.6×103 kg/m3×9.8 N/kg×0.76 m
= ρ水银 gh
=1.013×105 Pa
p大气=p水银
标准大气压 p0= 1.013×105 Pa
粗略计算标准大气压可取为105 Pa
大气压有多大
1.管内水银柱的高度和是否将玻璃管提起、
玻璃管的粗细、倾斜有关吗?
(无关。 p大气= p水银= ρ水银gh )
2.如果玻璃管顶部破了会怎么样?
(玻璃管内水银下降至与水槽内水银液面相平)
讨论一:
1.如果在实验中细管内不小心混进了一些空气,
则测量值比真实值_____. (偏大,偏小,不变)
偏小
2.如果在实验中,外界大气压突然变小了,则玻璃
管中的水银柱高度将_____. (变大,变小,不变)
变小
讨论二:
一个油罐的表面积约为200m2,标准大气压取105 Pa,大气压对油罐的压力有多大?这么大的压力为什么没把油罐压瘪呢?抽去油罐里的空气会怎样?
想想议议1:
抽去油罐里的空气会怎样
我们人体每时每刻都承受着大气压作用,
为什么没有被压瘪呢?
想想议议2:
大气压的应用
观看视频
记下视频中介绍的大气压有哪些应用?
大气压的应用
究竟是吸上来的还是大气压上来的呢?
吸管吸饮料
没有大气压会怎样?
小结
一大气压产生的原因是
二 大气压方向特点
三 证实大气压存在的著名实验
马德堡半球实验
四 最早测出大气压值的实验
标准大气压的值是
粗略计算取
大气受到重力和具有流动性
向各个方向都有压强
托里拆利实验
1.013×105Pa
105 Pa
1.把装满水的试管浸入水中,口朝下如图那样抓住管底向上提,在管口离开水面前,试管露出水面的部分( )
A 是空的 B 有水,但不满
C 充满水 D 以上都有可能
C
2、在冬天,保温瓶未装满水,当瓶内温度下降时软木塞不易拔出,这主要是( )
A、塞子与瓶口间摩擦力太大
B、瓶口遇冷收缩
C、瓶内气压小于大气压
D、原先塞子塞的太紧
C
3、一同学在标准大气压下做托里拆利实验,测得管中水银面比槽里水银面高750毫米,他失败的原因( )
A管子粗了一些。
B管子长了一些
C管子不在竖直位置。
D管中漏入少量空气。
D
谢 谢
