2012届福建省高考数学研讨会材料--强调应用
文档属性
| 名称 | 2012届福建省高考数学研讨会材料--强调应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-29 00:00:00 | ||
图片预览


文档简介
强调应用
一、学科内应用
例1 (2009福建单科质检文12)
已知函数f(x)=1-,x∈[0,1],对于满足0<<1的任意、,给出下列结论:
①(-)[f()-f()]<0; ② f()③f()-f()>-; ④
其中正确结论的序号 ( )
A.①② B.①③ C.②④ D.③④
例2 (2009福建质检理20)
已知函数.
(Ⅰ)求函数的极值;
(Ⅱ)对于曲线上的不同两点,,如果存在曲线上的点,且,使得曲线在点处的切线∥,则称为弦的伴随切线。特别地,当时,又称为的λ-伴随切线。
(ⅰ)求证:曲线的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ⅱ)是否存在曲线C,使得曲线C的任意一条弦均有伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
例3(2010福建质检理10).
已知是定义在上的函数,其图像是一条连续不断的曲线,且满足下列条件:
①的值域为,且;
②对任意不同的,都有.
那么关于的方程在上的根的情况是
A .没有实数根 B.有且只有一个实数根
C.恰有两个不同的实数根 D.有无数个不同的实数根
例4(2011福建质检文12)
已知函数.设是函数的零点的最大值,则下述论断一定错误的是
A. B. C. D.
例5(2011福建质检理9)
函数的图像上关于轴对称的点共有
A. 0对 B. 1 对 C. 2对 D. 3对
相关链接
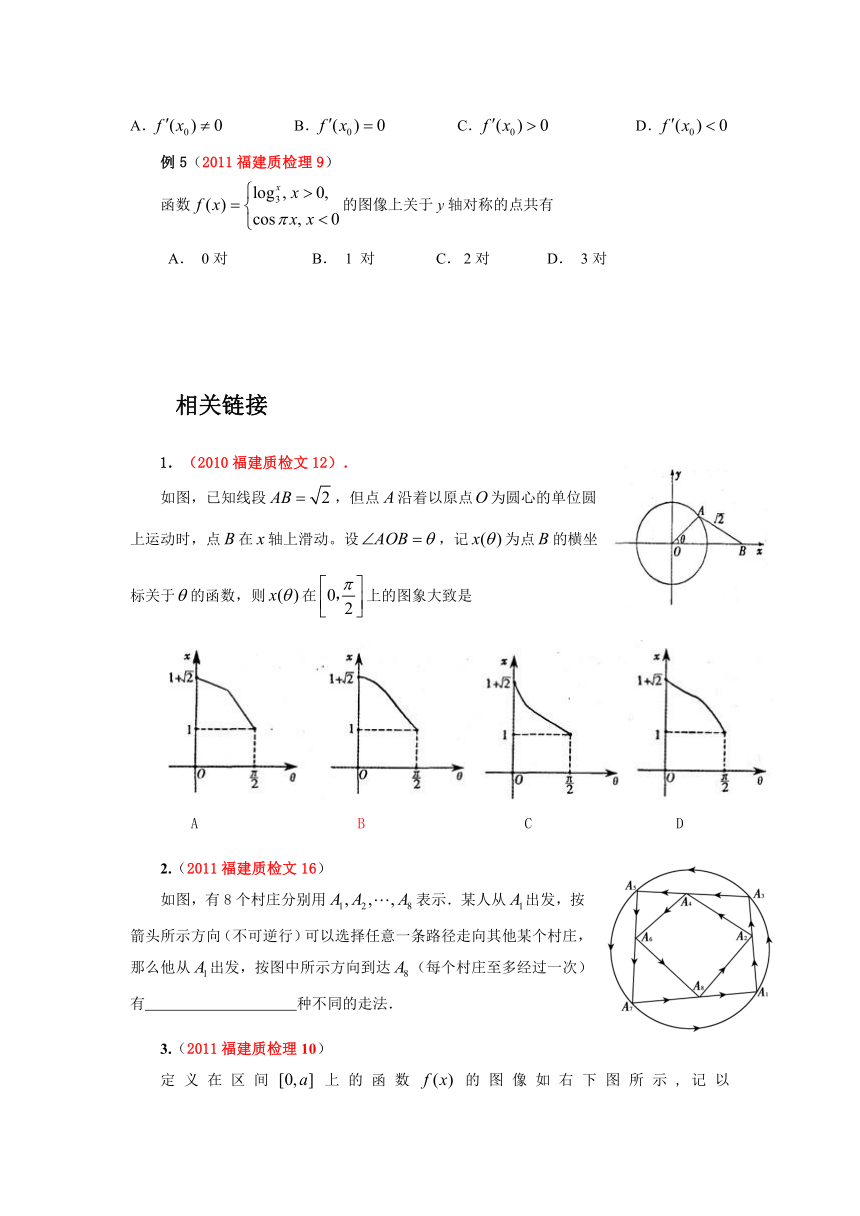
1.(2010福建质检文12).
如图,已知线段,但点沿着以原点为圆心的单位圆
上运动时,点在轴上滑动。设,记为点的横坐
标关于的函数,则在上的图象大致是
A B C D
2.(2011福建质检文16)
如图,有8个村庄分别用表示.某人从出发,按箭头所示方向(不可逆行)可以选择任意一条路径走向其他某个村庄,那么他从出发,按图中所示方向到达(每个村庄至多经过一次)有 种不同的走法.
3.(2011福建质检理10)
定义在区间上的函数的图像如右下图所示,记以为顶点的三角形的面积为,则函数的导函数的图像大致是
二、实际应用
例1 (2009福建单科质检理19)
已知某企业原有员工2000人,每人每年可为企业创利润3.5万元.为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的5%,并且每年给每位待岗员工发放生活补贴O.5万元.据评估,当待岗员工人数x不超过原有员工1%时,留岗员工每人每年可为企业多创利润(1-)万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利润O.9595万元.为使企业年利润最大,应安排多少员工待岗
例2(2009福建质检理17)
甲、乙两位学生参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参
加合适?请说明理由;
(Ⅲ)若将频率视为概率,对甲同学在今后的3次数学竞赛成绩进行预测,记这3次成
绩中高于80分的次数为,求的分布列及数学期望.
例3(2010福建质检理9)
今有甲、乙、丙、丁四人通过“拔河”进行“体力”较量.当甲、乙两人为一方,丙、丁两人为另一方时,双方势均力敌;当甲与丙对调之后,甲、丁一方轻易举战胜了乙、丙一方;而乙凭其一人之力便战胜了甲、丙两人的组合,那么,甲、乙、丙、丁四人的“体力”由强到弱的顺序是
A.丁、乙、甲、丙 B.乙、丁、甲、丙
C.丁、乙、丙、甲 D.乙、丁、丙、甲
例4(2010福建质检理18)
某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作.比赛时每运动员自选一个系列完成,两个动作得分之和为该运动员的成绩.假设每个运动员完成每个系列中的两个动作的得分是相互独立.根据赛前训练的统计数据,某运动员完成甲系列和乙系列动作的情况如下表:
表1:甲系列 表2:乙系列
动作 K动作 D动作
得分 100 80 40 10
概率
动作 K动作 D动作
得分 90 50 20 0
概率
现该运动员最后一个出场,之前其他运动员的最高得分为115分。
(Ⅰ)若该运动员希望获得该项目的第一名,应选择哪个系列?说明理由,并求其获得第一名的概率;
(Ⅱ)若该运动员选择乙系列,求其成绩的分布列及其数学期望.
例5(2011福建质检文20)
国家“十二五”规划纲要把保障和改善民生作为出发点和落脚点. “十二五”时期将提高住房保障水平,使城镇保障性住房覆盖率达到20%左右. 某城市2010年底有商品房万套,保障性住房万套. 预计2011年新增商品房万套,以后每年商品房新增量是上一年新增量的2倍. 问“十二五”时期(2011年2015年)该城市保障性住房建设年均应增加多少万套才能使覆盖率达到20%?(保障性住房覆盖率=,)
例6(2011福建质检理15)
某棋赛采用单循环赛(每两名选手均比赛一盘)方式进行,并规定:每盘胜者得1分,负者得0分,平局各得分.今有8位选手参加这项比赛,已知他们的得分互不相等,且按得分从高到低排名后,第二名选手的得分恰好是最后四名的得分之和.以下给出五个判断:
①第二名选手得分必不多于分;
②第二名选手得分必不少于分;
③第二名选手得分一定是分;
④第二名选手得分可能是分;
⑤第二名选手得分可能是分.
其中正确的判断的序号是 (填写所有正确判断的序号).
例7(2011福建质检理17)
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别对甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
(Ⅰ)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为,求的分布列和数学期望;
(Ⅱ)根据频率分布直方图填写下面列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关.
甲班(A方式) 乙班(B方式) 总计
成绩优秀
成绩不优秀
总计
附:(此公式也可写成)
0.25 0.15 0.10 0.05 0.025
1.323 2.072 2.706 3.840 5.024
相关链接
1.(2009福建质检文18)
甲、乙两位学生参加数学竞赛培训,在活动期间,,他们参加的5次测试成绩记录如下:
甲 82 82 79 95 87
乙 95 75 80 90 85
(Ⅰ)用茎叶图表示这两组数据;
(II)从甲、乙两人的成绩中各随机抽取一次,求甲的成绩比乙高的概率.
(III)若要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由;
2.(2009福建质检文20)
国家汽车产业振兴规划的政策极大地刺激了小排量汽车的销售.据分析预测,某地今年小排量型车每月的销量将以10%的增长率增长,小排量型车的销量每月递增20辆.已知该地今年1月份销售型车和型车均为60辆.据此推测,该地今年这两款车的销售总量能否超过3000辆 (参考数据:,,)
3.(2009福建单科质检理14)
某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
由表中数据算出线性回归方程中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为_________件.(参考公式:)
4.(2010福建质检文13)
为了解某地居民的月收入情况,一个社会调查机构调查了20000人,并根据所得数据画出样本的频率分布直方图,如图。现按月收入分层,用分层抽样的方法在这20000人中抽出200人作进一步调查,则月收入在(单位:元)的应抽取 人。
5.(2010福建质检文17)
某城市有连接8个小区、、、、、、、和
市中心的整齐方格形道路网,每个小方格均为正方形,如图。
某人从道路网中随机地选择一条最短路径,由小区前往。
(Ⅰ)列出此人从小区到的所有最短路径(自至依
次用所经过的小区的字母表示);
(Ⅱ)求他经过市中心的概率
6.(2010福建质检文16)
从甲、乙、丙、丁、戊、己6人中选出3人组成一个辩论赛队,要求满足如下三个条件:
①甲、丙两人中至少要选上一人;
②乙、戊两人中至少要选上一人;
③乙、丙两人中的每个人都不能与戊同时入选
如果乙未被选上,则一定入选的两人是 。
7.(2011福建质检文18)
某中学100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师用A、B两种不同的教学方式分别对甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名同学的成绩进行统计,作出茎叶图如下. 记成绩不低于90分者为“成绩优秀”.
(I)在乙班的20个样本中,现从不低于86分的成绩中随机抽取2个,求抽出的两个成绩均优秀的概率;
(II) 由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
甲班(A方式) 乙班(B方式) 总计
成绩优秀
成绩不优秀
总计
附:(此公式也可写成)
0.25 0.15 0.10 0.05 0.025
1.323 2.072 2.706 3.840 5.024
一、学科内应用
例1 (2009福建单科质检文12)
已知函数f(x)=1-,x∈[0,1],对于满足0<<1的任意、,给出下列结论:
①(-)[f()-f()]<0; ② f()
其中正确结论的序号 ( )
A.①② B.①③ C.②④ D.③④
例2 (2009福建质检理20)
已知函数.
(Ⅰ)求函数的极值;
(Ⅱ)对于曲线上的不同两点,,如果存在曲线上的点,且,使得曲线在点处的切线∥,则称为弦的伴随切线。特别地,当时,又称为的λ-伴随切线。
(ⅰ)求证:曲线的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ⅱ)是否存在曲线C,使得曲线C的任意一条弦均有伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
例3(2010福建质检理10).
已知是定义在上的函数,其图像是一条连续不断的曲线,且满足下列条件:
①的值域为,且;
②对任意不同的,都有.
那么关于的方程在上的根的情况是
A .没有实数根 B.有且只有一个实数根
C.恰有两个不同的实数根 D.有无数个不同的实数根
例4(2011福建质检文12)
已知函数.设是函数的零点的最大值,则下述论断一定错误的是
A. B. C. D.
例5(2011福建质检理9)
函数的图像上关于轴对称的点共有
A. 0对 B. 1 对 C. 2对 D. 3对
相关链接
1.(2010福建质检文12).
如图,已知线段,但点沿着以原点为圆心的单位圆
上运动时,点在轴上滑动。设,记为点的横坐
标关于的函数,则在上的图象大致是
A B C D
2.(2011福建质检文16)
如图,有8个村庄分别用表示.某人从出发,按箭头所示方向(不可逆行)可以选择任意一条路径走向其他某个村庄,那么他从出发,按图中所示方向到达(每个村庄至多经过一次)有 种不同的走法.
3.(2011福建质检理10)
定义在区间上的函数的图像如右下图所示,记以为顶点的三角形的面积为,则函数的导函数的图像大致是
二、实际应用
例1 (2009福建单科质检理19)
已知某企业原有员工2000人,每人每年可为企业创利润3.5万元.为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的5%,并且每年给每位待岗员工发放生活补贴O.5万元.据评估,当待岗员工人数x不超过原有员工1%时,留岗员工每人每年可为企业多创利润(1-)万元;当待岗员工人数x超过原有员工1%时,留岗员工每人每年可为企业多创利润O.9595万元.为使企业年利润最大,应安排多少员工待岗
例2(2009福建质检理17)
甲、乙两位学生参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参
加合适?请说明理由;
(Ⅲ)若将频率视为概率,对甲同学在今后的3次数学竞赛成绩进行预测,记这3次成
绩中高于80分的次数为,求的分布列及数学期望.
例3(2010福建质检理9)
今有甲、乙、丙、丁四人通过“拔河”进行“体力”较量.当甲、乙两人为一方,丙、丁两人为另一方时,双方势均力敌;当甲与丙对调之后,甲、丁一方轻易举战胜了乙、丙一方;而乙凭其一人之力便战胜了甲、丙两人的组合,那么,甲、乙、丙、丁四人的“体力”由强到弱的顺序是
A.丁、乙、甲、丙 B.乙、丁、甲、丙
C.丁、乙、丙、甲 D.乙、丁、丙、甲
例4(2010福建质检理18)
某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作.比赛时每运动员自选一个系列完成,两个动作得分之和为该运动员的成绩.假设每个运动员完成每个系列中的两个动作的得分是相互独立.根据赛前训练的统计数据,某运动员完成甲系列和乙系列动作的情况如下表:
表1:甲系列 表2:乙系列
动作 K动作 D动作
得分 100 80 40 10
概率
动作 K动作 D动作
得分 90 50 20 0
概率
现该运动员最后一个出场,之前其他运动员的最高得分为115分。
(Ⅰ)若该运动员希望获得该项目的第一名,应选择哪个系列?说明理由,并求其获得第一名的概率;
(Ⅱ)若该运动员选择乙系列,求其成绩的分布列及其数学期望.
例5(2011福建质检文20)
国家“十二五”规划纲要把保障和改善民生作为出发点和落脚点. “十二五”时期将提高住房保障水平,使城镇保障性住房覆盖率达到20%左右. 某城市2010年底有商品房万套,保障性住房万套. 预计2011年新增商品房万套,以后每年商品房新增量是上一年新增量的2倍. 问“十二五”时期(2011年2015年)该城市保障性住房建设年均应增加多少万套才能使覆盖率达到20%?(保障性住房覆盖率=,)
例6(2011福建质检理15)
某棋赛采用单循环赛(每两名选手均比赛一盘)方式进行,并规定:每盘胜者得1分,负者得0分,平局各得分.今有8位选手参加这项比赛,已知他们的得分互不相等,且按得分从高到低排名后,第二名选手的得分恰好是最后四名的得分之和.以下给出五个判断:
①第二名选手得分必不多于分;
②第二名选手得分必不少于分;
③第二名选手得分一定是分;
④第二名选手得分可能是分;
⑤第二名选手得分可能是分.
其中正确的判断的序号是 (填写所有正确判断的序号).
例7(2011福建质检理17)
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别对甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
(Ⅰ)从乙班随机抽取2名学生的成绩,记“成绩优秀”的个数为,求的分布列和数学期望;
(Ⅱ)根据频率分布直方图填写下面列联表,并判断是否有95%的把握认为:“成绩优秀”与教学方式有关.
甲班(A方式) 乙班(B方式) 总计
成绩优秀
成绩不优秀
总计
附:(此公式也可写成)
0.25 0.15 0.10 0.05 0.025
1.323 2.072 2.706 3.840 5.024
相关链接
1.(2009福建质检文18)
甲、乙两位学生参加数学竞赛培训,在活动期间,,他们参加的5次测试成绩记录如下:
甲 82 82 79 95 87
乙 95 75 80 90 85
(Ⅰ)用茎叶图表示这两组数据;
(II)从甲、乙两人的成绩中各随机抽取一次,求甲的成绩比乙高的概率.
(III)若要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由;
2.(2009福建质检文20)
国家汽车产业振兴规划的政策极大地刺激了小排量汽车的销售.据分析预测,某地今年小排量型车每月的销量将以10%的增长率增长,小排量型车的销量每月递增20辆.已知该地今年1月份销售型车和型车均为60辆.据此推测,该地今年这两款车的销售总量能否超过3000辆 (参考数据:,,)
3.(2009福建单科质检理14)
某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
由表中数据算出线性回归方程中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月毛衣的销售量约为_________件.(参考公式:)
4.(2010福建质检文13)
为了解某地居民的月收入情况,一个社会调查机构调查了20000人,并根据所得数据画出样本的频率分布直方图,如图。现按月收入分层,用分层抽样的方法在这20000人中抽出200人作进一步调查,则月收入在(单位:元)的应抽取 人。
5.(2010福建质检文17)
某城市有连接8个小区、、、、、、、和
市中心的整齐方格形道路网,每个小方格均为正方形,如图。
某人从道路网中随机地选择一条最短路径,由小区前往。
(Ⅰ)列出此人从小区到的所有最短路径(自至依
次用所经过的小区的字母表示);
(Ⅱ)求他经过市中心的概率
6.(2010福建质检文16)
从甲、乙、丙、丁、戊、己6人中选出3人组成一个辩论赛队,要求满足如下三个条件:
①甲、丙两人中至少要选上一人;
②乙、戊两人中至少要选上一人;
③乙、丙两人中的每个人都不能与戊同时入选
如果乙未被选上,则一定入选的两人是 。
7.(2011福建质检文18)
某中学100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师用A、B两种不同的教学方式分别对甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名同学的成绩进行统计,作出茎叶图如下. 记成绩不低于90分者为“成绩优秀”.
(I)在乙班的20个样本中,现从不低于86分的成绩中随机抽取2个,求抽出的两个成绩均优秀的概率;
(II) 由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
甲班(A方式) 乙班(B方式) 总计
成绩优秀
成绩不优秀
总计
附:(此公式也可写成)
0.25 0.15 0.10 0.05 0.025
1.323 2.072 2.706 3.840 5.024
同课章节目录
