2012届福建省高考数学研讨会材料--追求“开放”与“多样”
文档属性
| 名称 | 2012届福建省高考数学研讨会材料--追求“开放”与“多样” |

|
|
| 格式 | zip | ||
| 文件大小 | 280.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-29 00:00:00 | ||
图片预览

文档简介
追求“开放”与“多样”
例1(2009福建单科质检理17)——条件开放、选择性
记△ABC的三个内角A,B,C所对的边分别为a,b,c,向量,,且.
(Ⅰ)求A 的大小;
(Ⅱ)现给出下列四个条件:①a=1;②b=2sinB;③;④B=45°.
试从中再选择两个条件以确定ABC,并求出你所确定的ABC的面积.
(注:只需选择一个方案答题,如果用多种方案答题,则按第一种方案给分)
例2 (2009福建质检理17)——结论开放
甲、乙两位学生参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中
随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由;
(Ⅲ)若将频率视为概率,对甲同学在今后的3次数学竞赛成绩进行预测,记这3次成绩中高于80分的次数为,求的分布列及数学期望.
例3 (2009福建质检理20)——结论开放、解法开放、设问形式多样
已知函数.
(Ⅰ)求函数的极值;
(Ⅱ)对于曲线上的不同两点,,如果存在曲线上的点,且,使得曲线在点处的切线∥,则称为弦的伴随切线。特别地,当时,又称为的λ-伴随切线。
(ⅰ)求证:曲线的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ⅱ)是否存在曲线C,使得曲线C的任意一条弦均有伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
例4(2009福建质检理19)—— 解法开放
已知椭圆C的离心率,长轴的左右端点分
别为,。
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线与椭圆C交于P、Q两点,直线与交于点S。试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由。
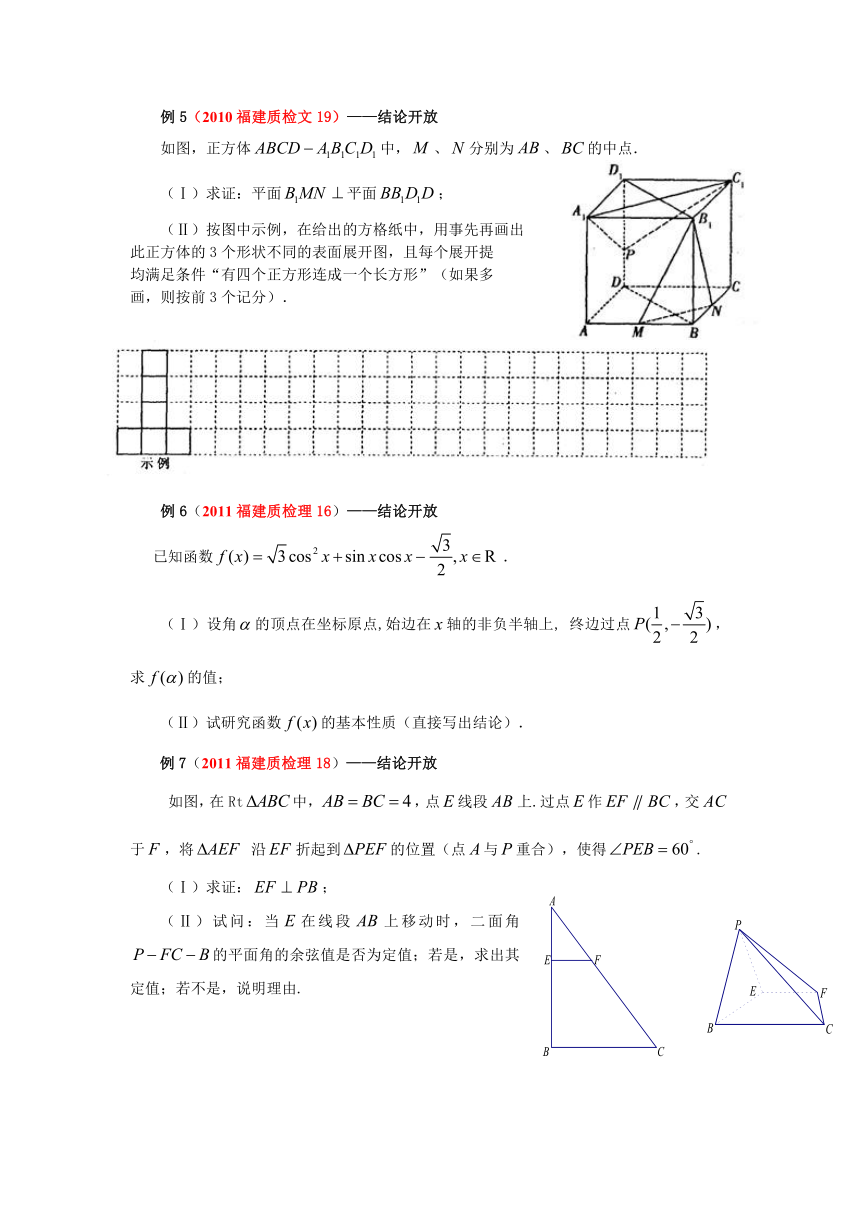
例5(2010福建质检文19)——结论开放
如图,正方体中,、分别为、的中点.
(Ⅰ)求证:平面平面;
(Ⅱ)按图中示例,在给出的方格纸中,用事先再画出
此正方体的3个形状不同的表面展开图,且每个展开提
均满足条件“有四个正方形连成一个长方形”(如果多
画,则按前3个记分).
例6(2011福建质检理16)——结论开放
已知函数.
(Ⅰ)设角的顶点在坐标原点,始边在轴的非负半轴上, 终边过点,求的值;
(Ⅱ)试研究函数的基本性质(直接写出结论).
例7(2011福建质检理18)——结论开放
如图,在Rt中,,点线段上.过点作,交于,将 沿折起到的位置(点与重合),使得.
(Ⅰ)求证:;
(Ⅱ)试问:当在线段上移动时,二面角的平面角的余弦值是否为定值;若是,求出其定值;若不是,说明理由.
例8(2011福建质检理20)——结论开放、解法开放、设问形式多样
已知椭圆的中心在原点,焦点在x轴上,离心率为,且过抛物线C:的焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)过坐标平面上的过点作抛物线C的两条切线和,它们分别交抛物线C的另一条切线于两点.
(ⅰ)若点恰好是点关于x轴的对称点,且与抛物线C的切点恰好为抛物线的顶点(如图)求证:的外接圆过点;
(ⅱ)试探究:若改变点的位置,或切线的位置,或抛物线C的开口大小,(ⅰ)中的结论是否仍然成立?由此给出一个使(ⅰ)中的结论成立的命题,并加以证明.(温馨提示:本小题将根据给出结论的一般性和综合性程度给分,但若给出的命题是假命题,本小题不得分)
相关链接
1.(2009考试说明样卷理19)—— 解法开放
以F1(0,-1),F2(0,1)为焦点的椭圆C过点P(,1).
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点S(,0)的动直线l交椭圆C于A、B两点,
试问:在坐标平面上是否存在一个定点T,使得无论l
如何转动,以AB为直径的圆恒过点T 若存在,求
出点T的坐标;若不存在,请说明理由.
2.(2009福建单科质检理21)—— 设问多样、解法开放
已知x=O是函数的一个极值点.
(I)求实数b的值;
(II)若函数恰有一个零点,求实数m的取值范围;
(III)当a=1时,函数的图象在处的切线与x轴的交点是(,0).若=1,,问是否存在等差数列{},使得对一切都成立 若存在,求出数列{}的通项公式;若不存在,请说明理由.
3.(2009福建单科质检理20)——设问形式多样
椭圆()的一个焦点在直线上,且离心率.
(Ⅰ)求椭圆方程;
(Ⅱ)如果、为椭圆上不同的两点,且弦的中点在直线上,试证:轴上存在定点,对于所有满足条件的、恒有;
(Ⅲ)在(Ⅱ)的条件,是否可能为等腰直角三角形?证明你的结论。
4.(2010福建质检理17)——条件开放、选择性
如图,是两条互相垂直的异面直线,点P、C在直线上,点A、B在直线上,M、N分别是线段AB、AP的中点,且PC=AC=,PA=
(Ⅰ)证明:PC⊥平面ABC;
(Ⅱ)设平面MNC与平面PBC所成的角为
现给出下列四个条件:
①CM=AB; ②AB=; ③CM⊥AB; ④BC⊥AC.
请你从中再选择两个条件以确定cos的值,并求之.
5.(2010福建质检文20)—— 解法开放
已知为递增的等比数列,且。
(Ⅰ)求数列的通项公式;
(Ⅱ)是否存在等差数列,使得对一切都成立?若存在,求出;若不存在,说明理由.
6.(2011福建质检文17)
设函数.
(Ⅰ)求的值;
(Ⅱ))试讨论函数的基本性质(直接写出结论).
7.(2011福建质检文22)——结论开放、解法开放、设问形式多样
已知抛物线()上一点到其焦点的距离为.
(Ⅰ)求抛物线的方程;
(Ⅱ)过坐标平面上的过点作抛物线C的两条切线和,分别交 分别交轴于两点.
(i) 若点的座标为,如图,求证:的外接圆过点;
(ii)试探究:若改变点的位置,或抛物线的开口大小,(i)中的结论是否依然成立 由此给出一个使(i)中结论成立的命题,并加以证明。(温馨提示:本小题将根据给出结论的一般性和综合性程度给分,但若给出的命题是假命题,本小题不得分)
例1(2009福建单科质检理17)——条件开放、选择性
记△ABC的三个内角A,B,C所对的边分别为a,b,c,向量,,且.
(Ⅰ)求A 的大小;
(Ⅱ)现给出下列四个条件:①a=1;②b=2sinB;③;④B=45°.
试从中再选择两个条件以确定ABC,并求出你所确定的ABC的面积.
(注:只需选择一个方案答题,如果用多种方案答题,则按第一种方案给分)
例2 (2009福建质检理17)——结论开放
甲、乙两位学生参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中
随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由;
(Ⅲ)若将频率视为概率,对甲同学在今后的3次数学竞赛成绩进行预测,记这3次成绩中高于80分的次数为,求的分布列及数学期望.
例3 (2009福建质检理20)——结论开放、解法开放、设问形式多样
已知函数.
(Ⅰ)求函数的极值;
(Ⅱ)对于曲线上的不同两点,,如果存在曲线上的点,且,使得曲线在点处的切线∥,则称为弦的伴随切线。特别地,当时,又称为的λ-伴随切线。
(ⅰ)求证:曲线的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ⅱ)是否存在曲线C,使得曲线C的任意一条弦均有伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
例4(2009福建质检理19)—— 解法开放
已知椭圆C的离心率,长轴的左右端点分
别为,。
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线与椭圆C交于P、Q两点,直线与交于点S。试问:当m变化时,点S是否恒在一条定直线上?若是,请写出这条直线方程,并证明你的结论;若不是,请说明理由。
例5(2010福建质检文19)——结论开放
如图,正方体中,、分别为、的中点.
(Ⅰ)求证:平面平面;
(Ⅱ)按图中示例,在给出的方格纸中,用事先再画出
此正方体的3个形状不同的表面展开图,且每个展开提
均满足条件“有四个正方形连成一个长方形”(如果多
画,则按前3个记分).
例6(2011福建质检理16)——结论开放
已知函数.
(Ⅰ)设角的顶点在坐标原点,始边在轴的非负半轴上, 终边过点,求的值;
(Ⅱ)试研究函数的基本性质(直接写出结论).
例7(2011福建质检理18)——结论开放
如图,在Rt中,,点线段上.过点作,交于,将 沿折起到的位置(点与重合),使得.
(Ⅰ)求证:;
(Ⅱ)试问:当在线段上移动时,二面角的平面角的余弦值是否为定值;若是,求出其定值;若不是,说明理由.
例8(2011福建质检理20)——结论开放、解法开放、设问形式多样
已知椭圆的中心在原点,焦点在x轴上,离心率为,且过抛物线C:的焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)过坐标平面上的过点作抛物线C的两条切线和,它们分别交抛物线C的另一条切线于两点.
(ⅰ)若点恰好是点关于x轴的对称点,且与抛物线C的切点恰好为抛物线的顶点(如图)求证:的外接圆过点;
(ⅱ)试探究:若改变点的位置,或切线的位置,或抛物线C的开口大小,(ⅰ)中的结论是否仍然成立?由此给出一个使(ⅰ)中的结论成立的命题,并加以证明.(温馨提示:本小题将根据给出结论的一般性和综合性程度给分,但若给出的命题是假命题,本小题不得分)
相关链接
1.(2009考试说明样卷理19)—— 解法开放
以F1(0,-1),F2(0,1)为焦点的椭圆C过点P(,1).
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点S(,0)的动直线l交椭圆C于A、B两点,
试问:在坐标平面上是否存在一个定点T,使得无论l
如何转动,以AB为直径的圆恒过点T 若存在,求
出点T的坐标;若不存在,请说明理由.
2.(2009福建单科质检理21)—— 设问多样、解法开放
已知x=O是函数的一个极值点.
(I)求实数b的值;
(II)若函数恰有一个零点,求实数m的取值范围;
(III)当a=1时,函数的图象在处的切线与x轴的交点是(,0).若=1,,问是否存在等差数列{},使得对一切都成立 若存在,求出数列{}的通项公式;若不存在,请说明理由.
3.(2009福建单科质检理20)——设问形式多样
椭圆()的一个焦点在直线上,且离心率.
(Ⅰ)求椭圆方程;
(Ⅱ)如果、为椭圆上不同的两点,且弦的中点在直线上,试证:轴上存在定点,对于所有满足条件的、恒有;
(Ⅲ)在(Ⅱ)的条件,是否可能为等腰直角三角形?证明你的结论。
4.(2010福建质检理17)——条件开放、选择性
如图,是两条互相垂直的异面直线,点P、C在直线上,点A、B在直线上,M、N分别是线段AB、AP的中点,且PC=AC=,PA=
(Ⅰ)证明:PC⊥平面ABC;
(Ⅱ)设平面MNC与平面PBC所成的角为
现给出下列四个条件:
①CM=AB; ②AB=; ③CM⊥AB; ④BC⊥AC.
请你从中再选择两个条件以确定cos的值,并求之.
5.(2010福建质检文20)—— 解法开放
已知为递增的等比数列,且。
(Ⅰ)求数列的通项公式;
(Ⅱ)是否存在等差数列,使得对一切都成立?若存在,求出;若不存在,说明理由.
6.(2011福建质检文17)
设函数.
(Ⅰ)求的值;
(Ⅱ))试讨论函数的基本性质(直接写出结论).
7.(2011福建质检文22)——结论开放、解法开放、设问形式多样
已知抛物线()上一点到其焦点的距离为.
(Ⅰ)求抛物线的方程;
(Ⅱ)过坐标平面上的过点作抛物线C的两条切线和,分别交 分别交轴于两点.
(i) 若点的座标为,如图,求证:的外接圆过点;
(ii)试探究:若改变点的位置,或抛物线的开口大小,(i)中的结论是否依然成立 由此给出一个使(i)中结论成立的命题,并加以证明。(温馨提示:本小题将根据给出结论的一般性和综合性程度给分,但若给出的命题是假命题,本小题不得分)
同课章节目录
