5.5 用二次函数解决问题 同步训练(含解析)
文档属性
| 名称 | 5.5 用二次函数解决问题 同步训练(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学苏科版九年级下册
5.5
用二次函数解决问题
同步训练
一、单选题(本大题共10题,每题3分,共30分)
1.国家实施”精准扶贫“政策以来,很多贫困人口走向了致富的道路.某地区2016年底有贫困人口9万人,通过社会各界的努力,2018年底贫困人口减少至1万人.设2016年底至2018年底该地区贫困人口的年平均下降率为
,根据题意列方程得(??
)
A.?????????????????????B.?????????????????????C.?????????????????????D.?
2.服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为( )
A.?150元?????????????????????????????????B.?160元?????????????????????????????????C.?170元?????????????????????????????????D.?180元
3.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )
A.?60m2??????????????????????????????????B.?63m2??????????????????????????????????C.?64m2??????????????????????????????????D.?66m2
4.某公园有一个圆形喷水池,喷出的水流呈抛物线,一条水流的高度h(单位:m)与水流运动时间t(单位:s)之间的关系式为h=30t﹣5t2
,
那么水流从抛出至回落到地面所需要的时间是(??
)
A.?6s?????????????????????????????????????????B.?4s?????????????????????????????????????????C.?3s?????????????????????????????????????????D.?2s
5.某旅游景点的收入受季节的影响较大,有时候出现赔本的经营状况.因此,公司规定:若无利润时,该景点关闭.经跟踪测算,该景点一年中的利润W(万元)与月份x之间满足二次函数W=﹣x2+16x﹣48,则该景点一年中处于关闭状态有(??
)月.
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
6.从地面竖直向上抛出一小球,小球的高度
h
(单位:
m
)与小球运动时间
(单位:
s
)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是
40m
;②小球运动的时间为
6s
;③小球抛出3秒时,速度为0;
④当
时,小球的高度
.其中正确的是(???
)
A.?①④????????????????????????????????????B.?①②????????????????????????????????????C.?②③④????????????????????????????????????D.?②④
7.如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是(??
)
A.????????????????????????????????????????????B.?
C.?????????????????????????????????????????????D.?
8.如图,某隧道美化施工,横截面形状为抛物线y
=-
x2
+
8(单位:米),施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF
=
3:2,则脚手架高DE为( )
A.?7米??????????????????????????????????????B.?6.3米??????????????????????????????????????C.?6米??????????????????????????????????????D.?5米
9.图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=﹣
(x﹣80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为(???
)
?
A.?16
米?????????????????????????????B.?米?????????????????????????????C.?16
米?????????????????????????????D.?米
10.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是
,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有(?
)
A.?1个????????????????????????????????????????B.?2个????????????????????????????????????????C.?3个????????????????????????????????????????D.?4
二、填空题(本大题共8题,每题2分,共16分)
11.小明推铅球,铅球行进高度
与水平距离
之间的关系为
,则小明推球的成绩是________m.
12.把一个小球以20米/秒的速度竖直向上弹出,它在空中的高度h(米)与时间t(秒),满足关系:h=20t-5t2
,
当小球达到最高点时,小球的运动时间为第________秒时.
13.如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,则水流的落地点C到水枪底部B的距离为________.
14.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为________.
15.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为
,两侧距底面
高处各有一盏灯,两灯间的水平距离为
,则这个隧道入口的最大高度为________
.
16.一养鸡专业户计划用116m长的篱笆围成如图所示的三间长方形鸡舍,门MN宽2m,门PQ和RS的宽都是1m,围成的鸡舍面积最大是________平方米.
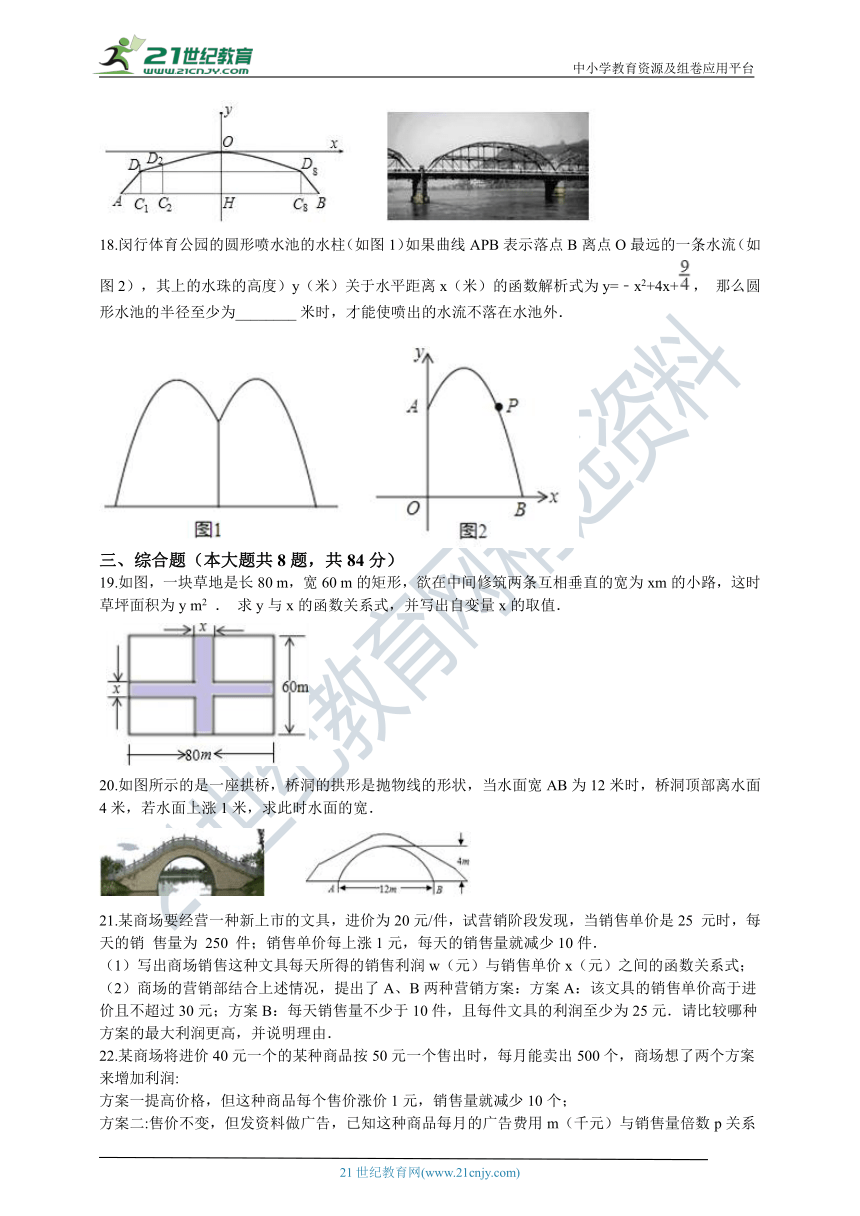
17.如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.
18.闵行体育公园的圆形喷水池的水柱(如图1)如果曲线APB表示落点B离点O最远的一条水流(如图2),其上的水珠的高度)y(米)关于水平距离x(米)的函数解析式为y=﹣x2+4x+,
那么圆形水池的半径至少为________?米时,才能使喷出的水流不落在水池外.
三、综合题(本大题共8题,共84分)
19.如图,一块草地是长80
m,宽60
m的矩形,欲在中间修筑两条互相垂直的宽为xm的小路,这时草坪面积为y
m2
.
求y与x的函数关系式,并写出自变量x的取值.
20.如图所示的是一座拱桥,桥洞的拱形是抛物线的形状,当水面宽AB为12米时,桥洞顶部离水面4米,若水面上涨1米,求此时水面的宽.
?
21.某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现,当销售单价是25
元时,每天的销
售量为
250
件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)商场的营销部结合上述情况,提出了A、B两种营销方案:方案A:该文具的销售单价高于进价且不超过30元;方案B:每天销售量不少于10件,且每件文具的利润至少为25元.请比较哪种方案的最大利润更高,并说明理由.
22.某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个,商场想了两个方案来增加利润:
方案一提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告,已知这种商品每月的广告费用m(千元)与销售量倍数p关系为p=-0.4m2+2m,
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由.
23.某服装厂生产A品种服装,每件成本为71元,零售商到此服装厂一次性批发A品牌服装x件时,批发单价为y元,y与x之间满足如下图所示的函数关系,其中批发件数x为10的正整数倍.
(1)当100≤x≤300
时,则y与x的函数关系式为________;
(2)某零售商到此服装厂一次性批发A品牌服装200件,需要支付________元;
(3)若零售商到此服装厂一次性批发A品牌服装x(100≤x≤400)
件,服装厂的利润为w元,求:x
为何值时,w最大?最大值是多少?
24.“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量
(件)与销售单价
(元)之间存在一次函数关系,如图所示.
(1)求
与
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
25.某商店销售一种进价50元/件的商品,经市场调查发现:该商品的每天销售量y(件)是售价x(元/件)的一次函数,其售价、销售量的二组对应值如下表:
售价x(元/件)
55
65
销售量y(件/天)
90
70
(1)若某天销售利润为800元,求该天的售价为多少元/件.
(2)由于某种原因,该商品进价提高了a元/件(a>0),商店售价不低于进价,物价部门规定该商品售价不得超过70元件,该商店在今后的销售中,每天能获得的销售最大利润是960元,求a的值.
26.如图1,地面BD上两根等长立柱AB,CD之问悬挂一根近似成抛物线y=
x2-
x+3的绳子.
?????
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米.求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
答案解析部分
一、单选题
1.【答案】
B
【考点】二次函数的实际应用-百分率问题
解:设这两年全省贫困人口的年平均下降率为
,根据题意得:
,
故答案为:B.
【分析】设两年来的平均下降率为x,根据题意得到关于x的方程,进行计算求值即可。
2.【答案】
A
【考点】二次函数的实际应用-销售问题
解:设获得的利润为y元,由题意得:
?
∵a=﹣1<0
∴当x=150时,y取得最大值2500元.
故答案为:A
.
【分析】设获得的利润为y元,由题意得关于x的二次函数,配方,写成顶点式,利用二次函数的性质可得答案.
3.【答案】
C
【考点】二次函数的实际应用-几何问题
解:设BC=xm,则AB=(16﹣x)m,矩形ABCD面积为ym2
,
根据题意得:y=(16﹣x)x=﹣x2+16x=﹣(x﹣8)2+64,
当x=8m时,ymax=64m2
,
则所围成矩形ABCD的最大面积是64m2
.
故选C.
【分析】设BC=xm,表示出AB,矩形面积为ym2
,
表示出y与x的关系式,利用二次函数性质求出面积最大值即可.
4.【答案】
A
【考点】二次函数的实际应用-喷水问题
解:水流从抛出至回落到地面时高度h为0,
把h=0代入h=30t﹣5t2得:5t2﹣30t=0,
解得:t1=0(舍去),t2=6.
故水流从抛出至回落到地面所需要的时间6s.
故选A.
【分析】由于水流从抛出至回落到地面时高度h为0,把h=0代入h=30t﹣5t2即可求出t,也就求出了水流从抛出至回落到地面所需要的时间.
5.【答案】
A
【考点】二次函数的实际应用-销售问题
解:由W=﹣x2+16x﹣48,令W=0,则x2﹣16x+48=0,解得x=12或4,
∴不等式﹣x2+16x﹣48>0的解为,4<x<12,
∴该景点一年中处于关闭状态有5个月.
故答案为:A.
【分析】关闭状态时的利润即为w=0,可得关于x的一元二次方程,解方程可求得x的值;再结合不关闭状态即为w>0可得关于x的范围,则题意可求解.
6.【答案】
C
【考点】二次函数的实际应用-抛球问题
解:①由图象知小球在空中达到的最大高度是40m,故①不符合题意;
②当t=6时,高度为0,则运动时间是6s,故②符合题意;
③小球抛出3秒时达到最高点即速度为0,故③符合题意;
④设函数解析式为:h=a(t-3)2+40,
把O点(0,0)代入得
,
解得:
,
∴
,
当t=1.5时,
,
解得:h=30米,故④符合题意;
故答案为:C.
【分析】根据函数图像依次判断各选项即可.
7.【答案】
A
【考点】分段函数,根据实际问题列二次函数关系式,二次函数的实际应用-动态几何问题
解:设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y
∴当C从D点运动到E点时,即0?x?2时,y=
×2×2?
?(2?x)×(2?x)=?
x?+2x.
当A从D点运动到E点时,即2×[2?(x?2)]×[2?(x?2)]=
x??4x+8
∴y与x之间的函数关系
由函数关系式可看出A中的函数图象与所求的分段函数对应。
故答案为:A.
【分析】根据已知观察图像,可知此题分两段求解,即当C从D点运动到E点时,即0?x?2时;当A从D点运动到E点时,即28.【答案】
C
【考点】二次函数的实际应用-拱桥问题
解:设EF=2k,
EF=3k,
∴OF=k,
∴G(k,3k),
∴3k=
-??k2?+
8?,
∴k2+6k-16=0,
∴(k+8)(k-2)=0,
∴k=-8(舍去),
或k=2,
∴DE=3k=6(米).
故答案为:C.
【分析】设EF=2k,
EF=3k,
把G的坐标用含k的代数式表示,
代入函数式求出求出k值,则脚手架高DE可求.
9.【答案】
B
【考点】二次函数的实际应用-拱桥问题
解:∵AC⊥x轴,OA=10米,
∴点C的横坐标为﹣10,
当x=﹣10时,y=﹣
(x﹣80)2+16=﹣
(﹣10﹣80)2+16=﹣
,
∴C(﹣10,﹣
),∴桥面离水面的高度AC为
m.
故答案为:B.
【分析】根据图象求出点C的横坐标,再将-10代入抛物线解析式计算即可。
10.【答案】
D
【考点】二次函数的实际应用-喷水问题
解:当x=0时,y=3,故柱子OA的高度为3m;(1)正确;
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点是(1,4),
故喷出的水流距柱子1m处达到最大高度,喷出的水流距水平面的最大高度是4米;故(2)(3)正确;
解方程-x2+2x+3=0,
得x1=-1,x2=3,
故水池的半径至少要3米,才能使喷出的水流不至于落在水池外,(4)正确.
故答案为:D.
【分析】根据已知抛物线的解析式,利用其性质,求出顶点坐标,抛物线与x轴、y轴的交点,再逐一判断即可解答。
二、填空题
11.【答案】
10
【考点】二次函数的实际应用-抛球问题
解:令函数式
中y=0,得
,
解得x1=10,x2=-2(舍去).
即铅球推出的距离是10m.
故答案为:10.
【分析】根据铅球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
12.【答案】
2
【考点】二次函数的实际应用-抛球问题
解:h=20t-5t2=-5(t-2)2+20,
∵-5<0,∴函数有最大值,
则当t=2时,球的高度最高.
故答案为2.
【分析】根据二次函数的性质解答即可.
13.【答案】
【考点】二次函数的实际应用-喷水问题
解:如图,
∵喷水口A距地面2m,
∴点A(0,2),
∵如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,
∴抛物线的顶点坐标为(2,3),
设抛物线的解析式为:y=a(x-2)2+3.
∴4a+3=2
解之:a=-
∴
当y=0时,
解之:x=(取正值).
故答案为:.
【分析】以点B为坐标原点建立平面直角坐标系,可得到点A,P的坐标,利用待定系数法求出抛物线的解析式;再求出当y=0时的x的值,根据点C的坐标,可得到点C到点B的距离。
14.【答案】0<a≤5
【考点】二次函数的实际应用-销售问题
解:设未来30天每天获得的利润为y,
y=(110-40-t)(20+4t)﹣(20+4t)a
化简,得
y=﹣4t2+(260-4a)t+1400﹣20a
每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,
∴
≥﹣4×302+×30+1400﹣20a
解得,a≤5,
又∵a>0,
即a的取值范围是:0<a≤5
【分析】设未来30天每天获得的利润为y,则每天销售的数量为:(20+4t)件,每件的利润为(110-40-t)元,销售商品所获得的利润为(110-40-t)(20+4t)元,需要缴纳电商平台推广费(20+4t)a元,根据每天实际获得的利润等于销售商品获得的利润减去需要缴纳电商平台推广费列出函数关系式,根据题意列出不等式,求解得出a的取值范围。
15.【答案】
【考点】二次函数的实际应用-拱桥问题
解:如图,建立平面直角坐标系,
设抛物线解析式为:
,
设
,
,
将点A和点B代入解析式,得
,解得
,
∴
,
,
则最大高度是
.
故答案为:
.
【分析】建立平面直角坐标系,设解析式为
,
将点
,
代入解析式,求出a和m的值,求出点B的坐标,点B的纵坐标的绝对值就是隧道的最大高度.
16.【答案】
450
【考点】二次函数的实际应用-几何问题
解:设鸡舍面积为y平方米,AB=xm,则AD=
+1=(60﹣2x)m
由题意得:y=x(60﹣2x)=﹣2x2+60x
∴当x=﹣
=15时,围成的鸡舍面积最大,最大值为:﹣2×152+60×15=450(平方米)
故答案为:450.
【分析】根据矩形面积=长宽可列出面积y与AB的长x之间的函数关系式,并将这个函数解析式配成顶点式结合二次函数的性质即可求解.
17.【答案】
7.24
【考点】二次函数的实际应用-拱桥问题
解:设抛物线D1OD8的解析式为y=ax2
,
将x=-13,y=-1.69代入,解得a=-
∵横梁D1D8=C1C8=AB-2AC1=36m
∴点D1的横坐标是-18,代入y=-
x2里可得y=3.24
又∵∠A=45°,
∴D1C1=AC1=4m
∴OH=3.24+4=7.24m.
【分析】根据函数图像设抛物线D1OD8的解析式为y=ax2
,
将x=-13,y=-1.69代入建立关于a的方程,解方程求出a的值,根据题意可得到点D1的横坐标是-18,将其代入函数解析式可求出对应的函数值,再求出D1C1=AC1=4m,然后求出OH的长。
18.【答案】
【考点】二次函数的实际应用-喷水问题
解:当y=0时,即﹣x2+4x+=0,
解得x1=,
x2=﹣(舍去).
答:水池的半径至少米时,才能使喷出的水流不落在水池外.
故答案为:.
【分析】根据二次函数的解析式求得抛物线与x轴的交点坐标的横坐标,即为所求的结果.
三、综合题
19.【答案】
解:依题意得把两条路分别进行平移,
长为80m的路移动到上方,长为60m的路移动左方,
∴草坪就变成了边长为(80﹣x)和(60﹣x)的长方形,
∴y=(80﹣x)(60﹣x)=x2﹣140x+4800,
自变量的取值应大于等于0,但应小于60,即0<x<60.
故填空答案:y=(80﹣x)(60﹣x)=x2﹣140x+4800(0<x<60).
【考点】二次函数的实际应用-几何问题
分析:由题意可得,除去道路后,
草坪就变成了边长为(80﹣x)和(60﹣x)的长方形,所以可得
y=(80﹣x)(60﹣x)
,整理即可求解。
?
20.【答案】
解:如图,以抛物线的顶点为原点,建立平面直角坐标系.
由题意可知抛物线过点(6,-4)
设抛物线的函数表达式为:
把(6,-4)代入
,可得
则抛物线的函数表达式为:
当水面上涨1米,水面所在的位置为直线
令
,则
,解得:
∴此时水面的宽为:6
米.
【考点】二次函数的实际应用-拱桥问题
分析:由题意建立适当的平面直角坐标系,用待定系数法可求抛物线的函数解析式,然后把
代入解析式即可求解.
21.【答案】
(1)解:根据题意得:
W=(x-20)[250-10(x-25)]=-10x2+700x-10000;
(2)解:∵W=-10x2+700x-10000=-10(x-35)2+2250
当x<35时W随x的增大而增大
A方案:20<x≤30,
∴当x=30时W最大值为-10×25+2250=2000;
B方案中,根据题意得:
解之:45≤x≤49
∵当x>35时y随x的增大而减小
∴当x=45时W最大值为-10×100+2250=1250
2000>1250
∴A种方案利润更高.
【考点】二次函数与不等式(组)的综合应用,二次函数的实际应用-销售问题
分析:(1)利用每天所得的销售利润w=每一件的利润×销售量,根据题意可得到W与x之间的函数解析式。
(2)将(1)中的函数解析式转化为顶点式,利用二次函数的性质可得到当x<35时W随x的增大而增大,可求出A方案中的最大利润;当x>35时y随x的增大而减小,列不等式组求出x的取值范围,从而可求出W的最大值,然后比较大小可得答案。
22.【答案】
解:设涨价x元,利润为y元,则①;y=(50十x-40)(500-10x)=-10x2+400x+5000=-10(x-20)2+9000,
∴方案一的最大利润为9000元②y=(50-40)×500p-1000m=-2000m2+9000m=-2000(x-2.25)2+10125,∴方案二的最大利润为10125元;
∴选择方案二能获得更大的利润.
【考点】二次函数的实际应用-销售问题
分析:根据利润y=每一件的利润×销售量,可得到y与x的函数解析式,再利用方案一求出最大利润;然后求出方案二的利润,比较大小可得答案。
23.【答案】
(1)
(2)18000
(3)解:当100≤x≤300时,
∵
<0,抛物线开口向下,
当x<195
时,w
随
x的增大而增大.
又x
为10的正整数倍,∴x=190时,w最大,最大值是3800.
当x>195
时,
w随x
的增大而减小.
又
x为10的正整数倍,∴x=200时,w
最大,最大值是3800.
当300<x≤400
时,
w=(80-71)x=9x.∵k=9>0,则w随x的增大而增大
∴x=400时,w
最大,最大值是3600.
?
∵3800>3600,∴当x=190
或x=200
时,w最大,最大值是3800.
【考点】一次函数的实际应用,二次函数的实际应用-销售问题
解:(2)当x=200
时,y=-20+110=90,200×90=18000元
即零售商一次性批发200件,需要支付18000元
【分析】(1)利用待定系数法求出一次函数解析式即可;
(2)当x=200时,代入?中,求出y的值,即得批发单价,根据总价=批发单价×数量200,即得结论;
(3)分别求出当100≤x≤300时,当300<x≤400
时,?y的最大值,然后比较即可.
24.【答案】
(1)解:由题意得:
.
故y与x之间的函数关系式为:y=-10x+700.
(2)解:由题意,得-10x+700≥240,
解得x≤46,
设利润为w=(x-30)?y=(x-30)(-10x+700),
w=-10x2+1000x-21000=-10(x-50)2+4000,
∵-10<0,
∴x<50时,w随x的增大而增大,
∴x=46时,w大=-10(46-50)2+4000=3840,
答:当销售单价为46元时,每天获取的利润最大,最大利润是3840元
(3)解:w-150=-10x2+1000x-21000-150=3600,
-10(x-50)2=-250,
x-50=±5,
x1=55,x2=45,
如图所示,由图象得:
当45≤x≤55时,捐款后每天剩余利润不低于3600元.
【考点】待定系数法求一次函数解析式,二次函数的最值,二次函数的实际应用-销售问题
分析:(1)用待定系数法求函数表达式,一次函数关系式可设y=kx+b。
(2)由利润=销售量×单件利润可以列出利润表达式,再通过二次函数的性质即可求出利润的最大值;
(3)首先根据利润w与单价x的表达式求出利润为3600元对应的x的值,再根据增减性即可求出销售单价x的范围。
25.【答案】
(1)解:依题意设y=kx+b,则有
,解得:
,
所以y=﹣2x+200,
若某天销售利润为800元,则(x﹣50)(﹣2x+200)=800,
解得:x1=60,x2=90,
该天的售价为60元或者90元;
(2)解:设总利润为w,根据题意得,
w=(x﹣50﹣a)(﹣2x+200)
=﹣2x2+(300+2a)x﹣10000﹣200a
∵a>0,∴对称轴x=
>75,∵﹣2<0,∴抛物线的开口向下,
∵x≤70,∴w随x的增大而增大,当x=70时,w最大=960,
即960=﹣2×702+(300+2a)×70﹣10000﹣200a,
解得:a=4.
【考点】一次函数的实际应用,二次函数的实际应用-销售问题
分析:(1)由已知可知y是x的一次函数,利用待定系数法求出一次函数的解析式,再由y=800,代入计算求出x的值即可。
(2)设总利润为w,根据总利润=每一件的利润×销售量,列出W与x之间的函数解析式,再利用二次函数的性质可求出a的值。
26.【答案】
(1)解:a=
>0,.抛物线顶点为最低点,
y=
x2-
x+3=
(x-4)2+
∴绳子最低点离地面的距离为
米
(2)解:由(1)可知,BD=8,
令x=0得y=3,,A(0,3),C(8,3),
由题意可得:抛物线F1的顶点坐标为:(2,1.8),
设F1的解析式为:y=a(x-2)2+1.8,
将(0,3)代入得:4a+1.8=3,
解得:a=0.3,
∴抛物线F1为:y=0.3(x-2)2+1.8
当x=3时,y=0.3×1+1.8=2.1,
∴MN的长度为:2.1米
(3)解:∵MN=DC=3,
∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上,
∴抛物线F2的顶点坐标为:(
m+4,k),
∴抛物线F2的解析式为:y=
(x-
m-4)2+k,
把C(8,3)代入得:
(x-
m-4)2+k=3,
解得:k=-
(4-
m)2+3,
∴k=-
(m-8)+3,
∴k是关于m的二次函数,
∴由已知m<8,在对称轴的左侧,
∴k随m的增大而增大,
∴当k-2时,-
(m-8)2+3=2,
16解得:m1=4,m2=12(不符合题意,舍去)
当k=2.5时,-
(m-8)2+3=2.5,
解得:m1=8-
,m2=8+2
(不符合题意,舍去),
当2≤k≤2.5时,m的取值范围是:4≤m≤8-2
【考点】二次函数的实际应用-拱桥问题
分析:(1)利用配方法将二次函数解析式化为顶点式,进而求出二次函数最值即可;
(2)利用顶点式求出抛物线F1的解析式,进而得出x=3时,y的值,即为MN的长;
(3)先利用抛物线的轴对称性可知抛物线F2的顶点在ND的垂直平分线上,据此设出抛物线F2的顶点坐标,并用顶点式表示出其解析式,然后利用待定系数法求出抛物线F2的解析式,从而可求出k的值,进而得出m的取值范围。?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
初中数学苏科版九年级下册
5.5
用二次函数解决问题
同步训练
一、单选题(本大题共10题,每题3分,共30分)
1.国家实施”精准扶贫“政策以来,很多贫困人口走向了致富的道路.某地区2016年底有贫困人口9万人,通过社会各界的努力,2018年底贫困人口减少至1万人.设2016年底至2018年底该地区贫困人口的年平均下降率为
,根据题意列方程得(??
)
A.?????????????????????B.?????????????????????C.?????????????????????D.?
2.服装店将进价为每件100元的服装按每件x(x>100)元出售,每天可销售(200﹣x)件,若想获得最大利润,则x应定为( )
A.?150元?????????????????????????????????B.?160元?????????????????????????????????C.?170元?????????????????????????????????D.?180元
3.如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )
A.?60m2??????????????????????????????????B.?63m2??????????????????????????????????C.?64m2??????????????????????????????????D.?66m2
4.某公园有一个圆形喷水池,喷出的水流呈抛物线,一条水流的高度h(单位:m)与水流运动时间t(单位:s)之间的关系式为h=30t﹣5t2
,
那么水流从抛出至回落到地面所需要的时间是(??
)
A.?6s?????????????????????????????????????????B.?4s?????????????????????????????????????????C.?3s?????????????????????????????????????????D.?2s
5.某旅游景点的收入受季节的影响较大,有时候出现赔本的经营状况.因此,公司规定:若无利润时,该景点关闭.经跟踪测算,该景点一年中的利润W(万元)与月份x之间满足二次函数W=﹣x2+16x﹣48,则该景点一年中处于关闭状态有(??
)月.
A.?5???????????????????????????????????????????B.?6???????????????????????????????????????????C.?7???????????????????????????????????????????D.?8
6.从地面竖直向上抛出一小球,小球的高度
h
(单位:
m
)与小球运动时间
(单位:
s
)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是
40m
;②小球运动的时间为
6s
;③小球抛出3秒时,速度为0;
④当
时,小球的高度
.其中正确的是(???
)
A.?①④????????????????????????????????????B.?①②????????????????????????????????????C.?②③④????????????????????????????????????D.?②④
7.如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是(??
)
A.????????????????????????????????????????????B.?
C.?????????????????????????????????????????????D.?
8.如图,某隧道美化施工,横截面形状为抛物线y
=-
x2
+
8(单位:米),施工队计划在隧道正中搭建一个矩形脚手架DEFG,已知DE:EF
=
3:2,则脚手架高DE为( )
A.?7米??????????????????????????????????????B.?6.3米??????????????????????????????????????C.?6米??????????????????????????????????????D.?5米
9.图2是图1中拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可近似看成抛物线y=﹣
(x﹣80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴,若OA=10米,则桥面离水面的高度AC为(???
)
?
A.?16
米?????????????????????????????B.?米?????????????????????????????C.?16
米?????????????????????????????D.?米
10.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是
,则下列结论:(1)柱子OA的高度为3m;(2)喷出的水流距柱子1m处达到最大高度;(3)喷出的水流距水平面的最大高度是4m;(4)水池的半径至少要3m才能使喷出的水流不至于落在池外.其中正确的有(?
)
A.?1个????????????????????????????????????????B.?2个????????????????????????????????????????C.?3个????????????????????????????????????????D.?4
二、填空题(本大题共8题,每题2分,共16分)
11.小明推铅球,铅球行进高度
与水平距离
之间的关系为
,则小明推球的成绩是________m.
12.把一个小球以20米/秒的速度竖直向上弹出,它在空中的高度h(米)与时间t(秒),满足关系:h=20t-5t2
,
当小球达到最高点时,小球的运动时间为第________秒时.
13.如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,则水流的落地点C到水枪底部B的距离为________.
14.某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0).未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元.通过市场调研发现,该时装单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为________.
15.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为
,两侧距底面
高处各有一盏灯,两灯间的水平距离为
,则这个隧道入口的最大高度为________
.
16.一养鸡专业户计划用116m长的篱笆围成如图所示的三间长方形鸡舍,门MN宽2m,门PQ和RS的宽都是1m,围成的鸡舍面积最大是________平方米.
17.如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.
18.闵行体育公园的圆形喷水池的水柱(如图1)如果曲线APB表示落点B离点O最远的一条水流(如图2),其上的水珠的高度)y(米)关于水平距离x(米)的函数解析式为y=﹣x2+4x+,
那么圆形水池的半径至少为________?米时,才能使喷出的水流不落在水池外.
三、综合题(本大题共8题,共84分)
19.如图,一块草地是长80
m,宽60
m的矩形,欲在中间修筑两条互相垂直的宽为xm的小路,这时草坪面积为y
m2
.
求y与x的函数关系式,并写出自变量x的取值.
20.如图所示的是一座拱桥,桥洞的拱形是抛物线的形状,当水面宽AB为12米时,桥洞顶部离水面4米,若水面上涨1米,求此时水面的宽.
?
21.某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现,当销售单价是25
元时,每天的销
售量为
250
件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)商场的营销部结合上述情况,提出了A、B两种营销方案:方案A:该文具的销售单价高于进价且不超过30元;方案B:每天销售量不少于10件,且每件文具的利润至少为25元.请比较哪种方案的最大利润更高,并说明理由.
22.某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个,商场想了两个方案来增加利润:
方案一提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告,已知这种商品每月的广告费用m(千元)与销售量倍数p关系为p=-0.4m2+2m,
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由.
23.某服装厂生产A品种服装,每件成本为71元,零售商到此服装厂一次性批发A品牌服装x件时,批发单价为y元,y与x之间满足如下图所示的函数关系,其中批发件数x为10的正整数倍.
(1)当100≤x≤300
时,则y与x的函数关系式为________;
(2)某零售商到此服装厂一次性批发A品牌服装200件,需要支付________元;
(3)若零售商到此服装厂一次性批发A品牌服装x(100≤x≤400)
件,服装厂的利润为w元,求:x
为何值时,w最大?最大值是多少?
24.“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量
(件)与销售单价
(元)之间存在一次函数关系,如图所示.
(1)求
与
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
25.某商店销售一种进价50元/件的商品,经市场调查发现:该商品的每天销售量y(件)是售价x(元/件)的一次函数,其售价、销售量的二组对应值如下表:
售价x(元/件)
55
65
销售量y(件/天)
90
70
(1)若某天销售利润为800元,求该天的售价为多少元/件.
(2)由于某种原因,该商品进价提高了a元/件(a>0),商店售价不低于进价,物价部门规定该商品售价不得超过70元件,该商店在今后的销售中,每天能获得的销售最大利润是960元,求a的值.
26.如图1,地面BD上两根等长立柱AB,CD之问悬挂一根近似成抛物线y=
x2-
x+3的绳子.
?????
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米.求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
答案解析部分
一、单选题
1.【答案】
B
【考点】二次函数的实际应用-百分率问题
解:设这两年全省贫困人口的年平均下降率为
,根据题意得:
,
故答案为:B.
【分析】设两年来的平均下降率为x,根据题意得到关于x的方程,进行计算求值即可。
2.【答案】
A
【考点】二次函数的实际应用-销售问题
解:设获得的利润为y元,由题意得:
?
∵a=﹣1<0
∴当x=150时,y取得最大值2500元.
故答案为:A
.
【分析】设获得的利润为y元,由题意得关于x的二次函数,配方,写成顶点式,利用二次函数的性质可得答案.
3.【答案】
C
【考点】二次函数的实际应用-几何问题
解:设BC=xm,则AB=(16﹣x)m,矩形ABCD面积为ym2
,
根据题意得:y=(16﹣x)x=﹣x2+16x=﹣(x﹣8)2+64,
当x=8m时,ymax=64m2
,
则所围成矩形ABCD的最大面积是64m2
.
故选C.
【分析】设BC=xm,表示出AB,矩形面积为ym2
,
表示出y与x的关系式,利用二次函数性质求出面积最大值即可.
4.【答案】
A
【考点】二次函数的实际应用-喷水问题
解:水流从抛出至回落到地面时高度h为0,
把h=0代入h=30t﹣5t2得:5t2﹣30t=0,
解得:t1=0(舍去),t2=6.
故水流从抛出至回落到地面所需要的时间6s.
故选A.
【分析】由于水流从抛出至回落到地面时高度h为0,把h=0代入h=30t﹣5t2即可求出t,也就求出了水流从抛出至回落到地面所需要的时间.
5.【答案】
A
【考点】二次函数的实际应用-销售问题
解:由W=﹣x2+16x﹣48,令W=0,则x2﹣16x+48=0,解得x=12或4,
∴不等式﹣x2+16x﹣48>0的解为,4<x<12,
∴该景点一年中处于关闭状态有5个月.
故答案为:A.
【分析】关闭状态时的利润即为w=0,可得关于x的一元二次方程,解方程可求得x的值;再结合不关闭状态即为w>0可得关于x的范围,则题意可求解.
6.【答案】
C
【考点】二次函数的实际应用-抛球问题
解:①由图象知小球在空中达到的最大高度是40m,故①不符合题意;
②当t=6时,高度为0,则运动时间是6s,故②符合题意;
③小球抛出3秒时达到最高点即速度为0,故③符合题意;
④设函数解析式为:h=a(t-3)2+40,
把O点(0,0)代入得
,
解得:
,
∴
,
当t=1.5时,
,
解得:h=30米,故④符合题意;
故答案为:C.
【分析】根据函数图像依次判断各选项即可.
7.【答案】
A
【考点】分段函数,根据实际问题列二次函数关系式,二次函数的实际应用-动态几何问题
解:设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y
∴当C从D点运动到E点时,即0?x?2时,y=
×2×2?
?(2?x)×(2?x)=?
x?+2x.
当A从D点运动到E点时,即2
x??4x+8
∴y与x之间的函数关系
由函数关系式可看出A中的函数图象与所求的分段函数对应。
故答案为:A.
【分析】根据已知观察图像,可知此题分两段求解,即当C从D点运动到E点时,即0?x?2时;当A从D点运动到E点时,即2
C
【考点】二次函数的实际应用-拱桥问题
解:设EF=2k,
EF=3k,
∴OF=k,
∴G(k,3k),
∴3k=
-??k2?+
8?,
∴k2+6k-16=0,
∴(k+8)(k-2)=0,
∴k=-8(舍去),
或k=2,
∴DE=3k=6(米).
故答案为:C.
【分析】设EF=2k,
EF=3k,
把G的坐标用含k的代数式表示,
代入函数式求出求出k值,则脚手架高DE可求.
9.【答案】
B
【考点】二次函数的实际应用-拱桥问题
解:∵AC⊥x轴,OA=10米,
∴点C的横坐标为﹣10,
当x=﹣10时,y=﹣
(x﹣80)2+16=﹣
(﹣10﹣80)2+16=﹣
,
∴C(﹣10,﹣
),∴桥面离水面的高度AC为
m.
故答案为:B.
【分析】根据图象求出点C的横坐标,再将-10代入抛物线解析式计算即可。
10.【答案】
D
【考点】二次函数的实际应用-喷水问题
解:当x=0时,y=3,故柱子OA的高度为3m;(1)正确;
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点是(1,4),
故喷出的水流距柱子1m处达到最大高度,喷出的水流距水平面的最大高度是4米;故(2)(3)正确;
解方程-x2+2x+3=0,
得x1=-1,x2=3,
故水池的半径至少要3米,才能使喷出的水流不至于落在水池外,(4)正确.
故答案为:D.
【分析】根据已知抛物线的解析式,利用其性质,求出顶点坐标,抛物线与x轴、y轴的交点,再逐一判断即可解答。
二、填空题
11.【答案】
10
【考点】二次函数的实际应用-抛球问题
解:令函数式
中y=0,得
,
解得x1=10,x2=-2(舍去).
即铅球推出的距离是10m.
故答案为:10.
【分析】根据铅球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
12.【答案】
2
【考点】二次函数的实际应用-抛球问题
解:h=20t-5t2=-5(t-2)2+20,
∵-5<0,∴函数有最大值,
则当t=2时,球的高度最高.
故答案为2.
【分析】根据二次函数的性质解答即可.
13.【答案】
【考点】二次函数的实际应用-喷水问题
解:如图,
∵喷水口A距地面2m,
∴点A(0,2),
∵如果水流的最高点P到喷水枪AB所在直线的距离为2m,且到地面的距离为3m,
∴抛物线的顶点坐标为(2,3),
设抛物线的解析式为:y=a(x-2)2+3.
∴4a+3=2
解之:a=-
∴
当y=0时,
解之:x=(取正值).
故答案为:.
【分析】以点B为坐标原点建立平面直角坐标系,可得到点A,P的坐标,利用待定系数法求出抛物线的解析式;再求出当y=0时的x的值,根据点C的坐标,可得到点C到点B的距离。
14.【答案】0<a≤5
【考点】二次函数的实际应用-销售问题
解:设未来30天每天获得的利润为y,
y=(110-40-t)(20+4t)﹣(20+4t)a
化简,得
y=﹣4t2+(260-4a)t+1400﹣20a
每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,
∴
≥﹣4×302+×30+1400﹣20a
解得,a≤5,
又∵a>0,
即a的取值范围是:0<a≤5
【分析】设未来30天每天获得的利润为y,则每天销售的数量为:(20+4t)件,每件的利润为(110-40-t)元,销售商品所获得的利润为(110-40-t)(20+4t)元,需要缴纳电商平台推广费(20+4t)a元,根据每天实际获得的利润等于销售商品获得的利润减去需要缴纳电商平台推广费列出函数关系式,根据题意列出不等式,求解得出a的取值范围。
15.【答案】
【考点】二次函数的实际应用-拱桥问题
解:如图,建立平面直角坐标系,
设抛物线解析式为:
,
设
,
,
将点A和点B代入解析式,得
,解得
,
∴
,
,
则最大高度是
.
故答案为:
.
【分析】建立平面直角坐标系,设解析式为
,
将点
,
代入解析式,求出a和m的值,求出点B的坐标,点B的纵坐标的绝对值就是隧道的最大高度.
16.【答案】
450
【考点】二次函数的实际应用-几何问题
解:设鸡舍面积为y平方米,AB=xm,则AD=
+1=(60﹣2x)m
由题意得:y=x(60﹣2x)=﹣2x2+60x
∴当x=﹣
=15时,围成的鸡舍面积最大,最大值为:﹣2×152+60×15=450(平方米)
故答案为:450.
【分析】根据矩形面积=长宽可列出面积y与AB的长x之间的函数关系式,并将这个函数解析式配成顶点式结合二次函数的性质即可求解.
17.【答案】
7.24
【考点】二次函数的实际应用-拱桥问题
解:设抛物线D1OD8的解析式为y=ax2
,
将x=-13,y=-1.69代入,解得a=-
∵横梁D1D8=C1C8=AB-2AC1=36m
∴点D1的横坐标是-18,代入y=-
x2里可得y=3.24
又∵∠A=45°,
∴D1C1=AC1=4m
∴OH=3.24+4=7.24m.
【分析】根据函数图像设抛物线D1OD8的解析式为y=ax2
,
将x=-13,y=-1.69代入建立关于a的方程,解方程求出a的值,根据题意可得到点D1的横坐标是-18,将其代入函数解析式可求出对应的函数值,再求出D1C1=AC1=4m,然后求出OH的长。
18.【答案】
【考点】二次函数的实际应用-喷水问题
解:当y=0时,即﹣x2+4x+=0,
解得x1=,
x2=﹣(舍去).
答:水池的半径至少米时,才能使喷出的水流不落在水池外.
故答案为:.
【分析】根据二次函数的解析式求得抛物线与x轴的交点坐标的横坐标,即为所求的结果.
三、综合题
19.【答案】
解:依题意得把两条路分别进行平移,
长为80m的路移动到上方,长为60m的路移动左方,
∴草坪就变成了边长为(80﹣x)和(60﹣x)的长方形,
∴y=(80﹣x)(60﹣x)=x2﹣140x+4800,
自变量的取值应大于等于0,但应小于60,即0<x<60.
故填空答案:y=(80﹣x)(60﹣x)=x2﹣140x+4800(0<x<60).
【考点】二次函数的实际应用-几何问题
分析:由题意可得,除去道路后,
草坪就变成了边长为(80﹣x)和(60﹣x)的长方形,所以可得
y=(80﹣x)(60﹣x)
,整理即可求解。
?
20.【答案】
解:如图,以抛物线的顶点为原点,建立平面直角坐标系.
由题意可知抛物线过点(6,-4)
设抛物线的函数表达式为:
把(6,-4)代入
,可得
则抛物线的函数表达式为:
当水面上涨1米,水面所在的位置为直线
令
,则
,解得:
∴此时水面的宽为:6
米.
【考点】二次函数的实际应用-拱桥问题
分析:由题意建立适当的平面直角坐标系,用待定系数法可求抛物线的函数解析式,然后把
代入解析式即可求解.
21.【答案】
(1)解:根据题意得:
W=(x-20)[250-10(x-25)]=-10x2+700x-10000;
(2)解:∵W=-10x2+700x-10000=-10(x-35)2+2250
当x<35时W随x的增大而增大
A方案:20<x≤30,
∴当x=30时W最大值为-10×25+2250=2000;
B方案中,根据题意得:
解之:45≤x≤49
∵当x>35时y随x的增大而减小
∴当x=45时W最大值为-10×100+2250=1250
2000>1250
∴A种方案利润更高.
【考点】二次函数与不等式(组)的综合应用,二次函数的实际应用-销售问题
分析:(1)利用每天所得的销售利润w=每一件的利润×销售量,根据题意可得到W与x之间的函数解析式。
(2)将(1)中的函数解析式转化为顶点式,利用二次函数的性质可得到当x<35时W随x的增大而增大,可求出A方案中的最大利润;当x>35时y随x的增大而减小,列不等式组求出x的取值范围,从而可求出W的最大值,然后比较大小可得答案。
22.【答案】
解:设涨价x元,利润为y元,则①;y=(50十x-40)(500-10x)=-10x2+400x+5000=-10(x-20)2+9000,
∴方案一的最大利润为9000元②y=(50-40)×500p-1000m=-2000m2+9000m=-2000(x-2.25)2+10125,∴方案二的最大利润为10125元;
∴选择方案二能获得更大的利润.
【考点】二次函数的实际应用-销售问题
分析:根据利润y=每一件的利润×销售量,可得到y与x的函数解析式,再利用方案一求出最大利润;然后求出方案二的利润,比较大小可得答案。
23.【答案】
(1)
(2)18000
(3)解:当100≤x≤300时,
∵
<0,抛物线开口向下,
当x<195
时,w
随
x的增大而增大.
又x
为10的正整数倍,∴x=190时,w最大,最大值是3800.
当x>195
时,
w随x
的增大而减小.
又
x为10的正整数倍,∴x=200时,w
最大,最大值是3800.
当300<x≤400
时,
w=(80-71)x=9x.∵k=9>0,则w随x的增大而增大
∴x=400时,w
最大,最大值是3600.
?
∵3800>3600,∴当x=190
或x=200
时,w最大,最大值是3800.
【考点】一次函数的实际应用,二次函数的实际应用-销售问题
解:(2)当x=200
时,y=-20+110=90,200×90=18000元
即零售商一次性批发200件,需要支付18000元
【分析】(1)利用待定系数法求出一次函数解析式即可;
(2)当x=200时,代入?中,求出y的值,即得批发单价,根据总价=批发单价×数量200,即得结论;
(3)分别求出当100≤x≤300时,当300<x≤400
时,?y的最大值,然后比较即可.
24.【答案】
(1)解:由题意得:
.
故y与x之间的函数关系式为:y=-10x+700.
(2)解:由题意,得-10x+700≥240,
解得x≤46,
设利润为w=(x-30)?y=(x-30)(-10x+700),
w=-10x2+1000x-21000=-10(x-50)2+4000,
∵-10<0,
∴x<50时,w随x的增大而增大,
∴x=46时,w大=-10(46-50)2+4000=3840,
答:当销售单价为46元时,每天获取的利润最大,最大利润是3840元
(3)解:w-150=-10x2+1000x-21000-150=3600,
-10(x-50)2=-250,
x-50=±5,
x1=55,x2=45,
如图所示,由图象得:
当45≤x≤55时,捐款后每天剩余利润不低于3600元.
【考点】待定系数法求一次函数解析式,二次函数的最值,二次函数的实际应用-销售问题
分析:(1)用待定系数法求函数表达式,一次函数关系式可设y=kx+b。
(2)由利润=销售量×单件利润可以列出利润表达式,再通过二次函数的性质即可求出利润的最大值;
(3)首先根据利润w与单价x的表达式求出利润为3600元对应的x的值,再根据增减性即可求出销售单价x的范围。
25.【答案】
(1)解:依题意设y=kx+b,则有
,解得:
,
所以y=﹣2x+200,
若某天销售利润为800元,则(x﹣50)(﹣2x+200)=800,
解得:x1=60,x2=90,
该天的售价为60元或者90元;
(2)解:设总利润为w,根据题意得,
w=(x﹣50﹣a)(﹣2x+200)
=﹣2x2+(300+2a)x﹣10000﹣200a
∵a>0,∴对称轴x=
>75,∵﹣2<0,∴抛物线的开口向下,
∵x≤70,∴w随x的增大而增大,当x=70时,w最大=960,
即960=﹣2×702+(300+2a)×70﹣10000﹣200a,
解得:a=4.
【考点】一次函数的实际应用,二次函数的实际应用-销售问题
分析:(1)由已知可知y是x的一次函数,利用待定系数法求出一次函数的解析式,再由y=800,代入计算求出x的值即可。
(2)设总利润为w,根据总利润=每一件的利润×销售量,列出W与x之间的函数解析式,再利用二次函数的性质可求出a的值。
26.【答案】
(1)解:a=
>0,.抛物线顶点为最低点,
y=
x2-
x+3=
(x-4)2+
∴绳子最低点离地面的距离为
米
(2)解:由(1)可知,BD=8,
令x=0得y=3,,A(0,3),C(8,3),
由题意可得:抛物线F1的顶点坐标为:(2,1.8),
设F1的解析式为:y=a(x-2)2+1.8,
将(0,3)代入得:4a+1.8=3,
解得:a=0.3,
∴抛物线F1为:y=0.3(x-2)2+1.8
当x=3时,y=0.3×1+1.8=2.1,
∴MN的长度为:2.1米
(3)解:∵MN=DC=3,
∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上,
∴抛物线F2的顶点坐标为:(
m+4,k),
∴抛物线F2的解析式为:y=
(x-
m-4)2+k,
把C(8,3)代入得:
(x-
m-4)2+k=3,
解得:k=-
(4-
m)2+3,
∴k=-
(m-8)+3,
∴k是关于m的二次函数,
∴由已知m<8,在对称轴的左侧,
∴k随m的增大而增大,
∴当k-2时,-
(m-8)2+3=2,
16解得:m1=4,m2=12(不符合题意,舍去)
当k=2.5时,-
(m-8)2+3=2.5,
解得:m1=8-
,m2=8+2
(不符合题意,舍去),
当2≤k≤2.5时,m的取值范围是:4≤m≤8-2
【考点】二次函数的实际应用-拱桥问题
分析:(1)利用配方法将二次函数解析式化为顶点式,进而求出二次函数最值即可;
(2)利用顶点式求出抛物线F1的解析式,进而得出x=3时,y的值,即为MN的长;
(3)先利用抛物线的轴对称性可知抛物线F2的顶点在ND的垂直平分线上,据此设出抛物线F2的顶点坐标,并用顶点式表示出其解析式,然后利用待定系数法求出抛物线F2的解析式,从而可求出k的值,进而得出m的取值范围。?
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
