六年级数学上册试题 一课一练《数学广角-数与形》习题-人教版(含答案)
文档属性
| 名称 | 六年级数学上册试题 一课一练《数学广角-数与形》习题-人教版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 119.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 00:00:00 | ||
图片预览


文档简介
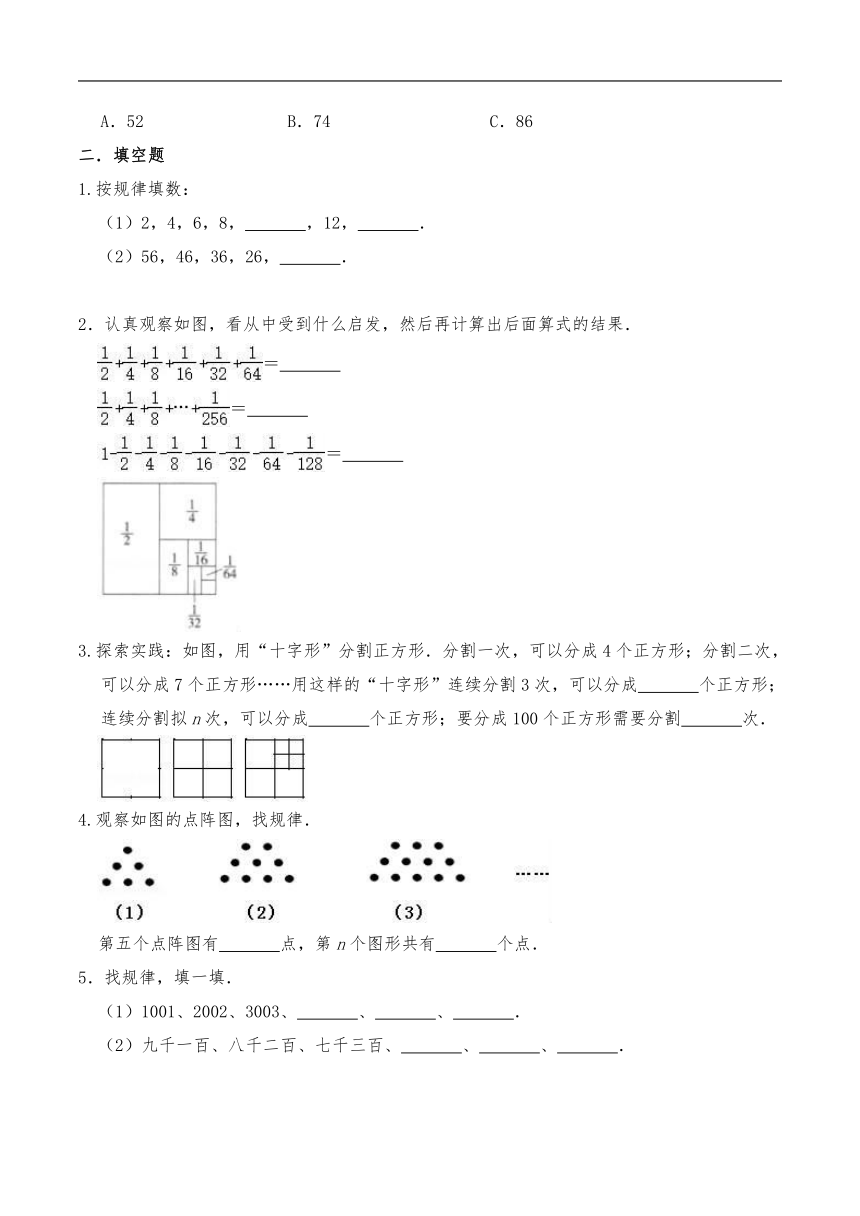
《数学广角-数与形》习题
一.选择题
1.根据1÷11=0.
,2÷11=0.
,3÷11=0.
,可以推出9÷11=( )
A.0.
B.0.
C.0.
D.0.
2.如图是用棋子摆成的图形,摆第一个图形需要3枚棋子,摆第二个图形需要6枚棋子,摆第三个图形需要9枚棋子……照这样的规律摆第11个图形需要( )枚棋子.
A.27
B.30
C.33
D.36
3.寒假的时候,同学们去莲花山滑雪场滑雪,有些同学用雪杖摆成了如图:
像上面那样摆10个三角形,至少需要( )根滑雪杖.
A.21
B.20
C.9
D.30
4.用小棒摆正六边形,(如图所示),按照这样的方法摆下去,摆n个正六边形需要( )小棒.
A.6n
B.5n
C.5n+1
D.6n+1
5.如图的每个正方形中的四个数之间都有相同的规律,请根据此规律,计算出m的值是( )
A.86
B.74
C.52
6.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,n等于( )
A.52
B.74
C.86
二.填空题
1.按规律填数:
(1)2,4,6,8,
,12,
.
(2)56,46,36,26,
.
2.认真观察如图,看从中受到什么启发,然后再计算出后面算式的结果.
=
=
=
3.探索实践:如图,用“十字形”分割正方形.分割一次,可以分成4个正方形;分割二次,可以分成7个正方形……用这样的“十字形”连续分割3次,可以分成
个正方形;连续分割拟n次,可以分成
个正方形;要分成100个正方形需要分割
次.
4.观察如图的点阵图,找规律.
第五个点阵图有
点,第n个图形共有
个点.
5.找规律,填一填.
(1)1001、2002、3003、
、
、
.
(2)九千一百、八千二百、七千三百、
、
、
.
6.现有若干个圆环,它们的外直径都是5厘米,环宽5毫米,将它们扣在一起(如图所示)拉紧后测量总长度.
圆环个数
1
2
3
4
…
总长度(cm)
5
9
13
17
…
像这样,10个圆环拉紧后的长度是
厘米.如果圆环的个数为n,拉紧后总长度是
厘米.
三.判断题
1.用小棒照图搭正方形,搭一个正方形用4根,搭两个正方形用7根,搭a个正方形有4a根.(
)
2.按1、8、27、
、125、216的规律排,横线中的数应为64.(
)
3.第五个点阵中点的个数是:1+4×4=17.(
)
4.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒.(
)
5.如图:
那么第7个点阵有45个点.(
)
四.应用题
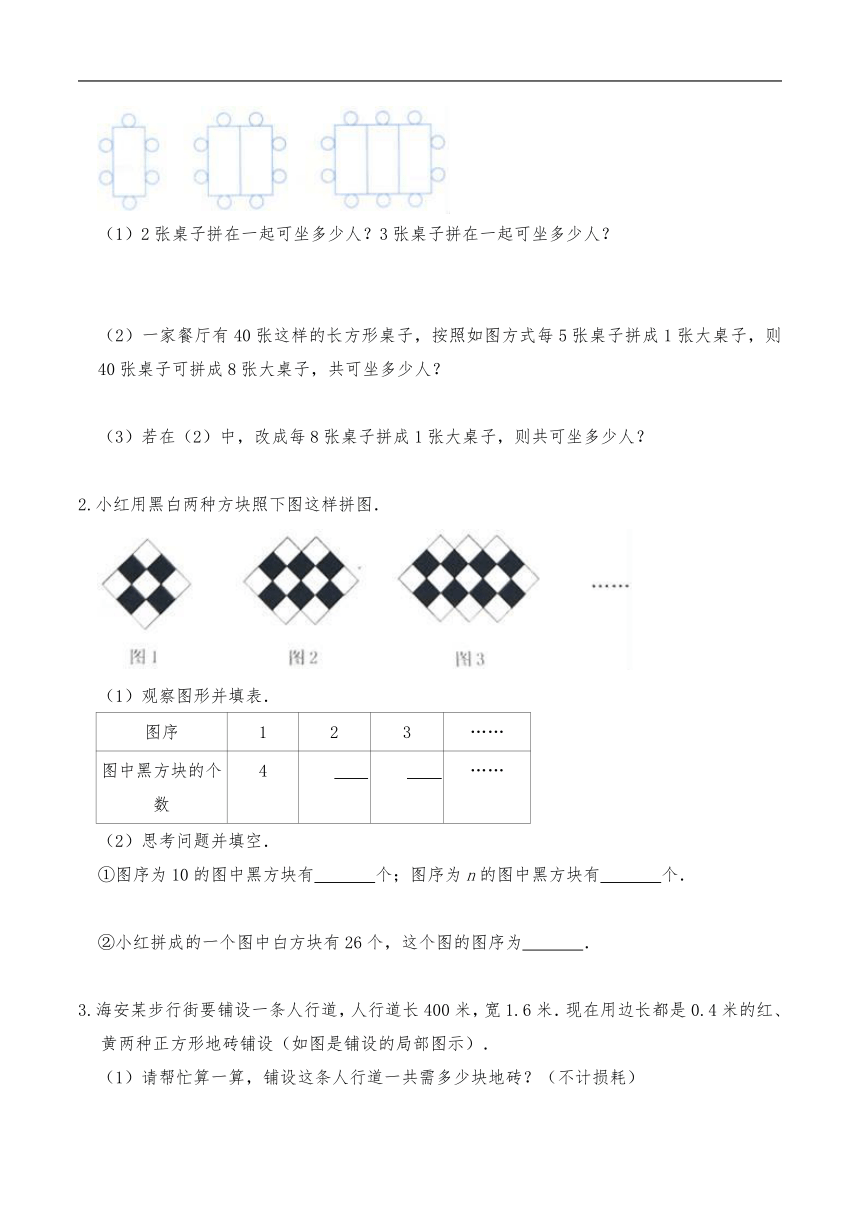
1.一张长方形桌子可坐6人,按下列方式将桌子拼在一起.
(1)2张桌子拼在一起可坐多少人?3张桌子拼在一起可坐多少人?
(2)一家餐厅有40张这样的长方形桌子,按照如图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)若在(2)中,改成每8张桌子拼成1张大桌子,则共可坐多少人?
2.小红用黑白两种方块照下图这样拼图.
(1)观察图形并填表.
图序
1
2
3
……
图中黑方块的个数
4
……
(2)思考问题并填空.
①图序为10的图中黑方块有
个;图序为n的图中黑方块有
个.
②小红拼成的一个图中白方块有26个,这个图的图序为
.
3.海安某步行街要铺设一条人行道,人行道长400米,宽1.6米.现在用边长都是0.4米的红、黄两种正方形地砖铺设(如图是铺设的局部图示).
(1)请帮忙算一算,铺设这条人行道一共需多少块地砖?(不计损耗)
(2)铺设这条人行道一共需要多少块红色地砖?(不计损耗)
4.如图,把同样大小的黑色棋子摆放在正多边形的边上,按这样的规律摆下去,第6个图形需要黑色棋子多少个?则第n(n是大于0的整数)个图形需要黑色棋子多少个?
5.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
6.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张这样的餐桌拼接起来,四周分别可坐
.
人:若把8张这样的餐桌拼接起来,四周分别可坐
人.
(2)若有餐的人数有90人,则这样的餐桌需要多少张?
答案
一.选择题
1.D.2.C.3.A.4.C.5.A.6.C.
二.填空题
1.10,14;16.
2.;;.
3.10;(3n+1);33.
4.18;3(n+1).
5.4004、5005、6006;六千四百、五千五百、四千六百.
6.41;(4n+1).
三.判断题
1.×.2.√.3.√.4.√.5.×.
四.应用题
1.解:(1)6+2=8(人)
6+2+2=10(人)
答:2张桌子拼在一起可坐8人;3张桌子拼在一起可坐10人.
(2)6+2+2+2+2=14(人)
8×14=112(人)
答:共可坐112人.
(3)6+2+2+2+2+2+2+2
=6+2×(8﹣1)
=6+14
=20(人)
40÷8×20
5×20
=100(人)
答:改成每8张桌子拼成1张大桌子,则共可坐100人.
2.解:(1)填表如下:
图序
1
2
3
……
图中黑方块的个数
4
6
8
……
(2)①图1黑色方块4个
图2黑色方块4+2=6(个)
图3黑色方块:4+2+2=8(个)
……
图10黑方块的个数:
2×10+2
=20+2
=22(个)
……
第n个图形黑色方块的个数为:4+2(n﹣1)=(2n+2)个
答:图序为10的图中黑方块有22个;图序为n的图中黑方块有(2n+2)个.
②白方块的排列规律为:
图1:5个
图2:5+3=9(个)
图3:5+3+3=11(个)
……
第n个图形白方块个数:5+3(n﹣1)=(3n+2)个
3n+2=26
3n=24
n=8
答:白方块有26个,这个图的图序为8.
故答案为:6,8;22,(2n+2);8.
3.解:(1)400×1.6÷0.42
=640÷0.16
=4000(块)
答:铺设这条人行道一共需4000块地砖.
(2)4000÷16×4
=250×4
=1000(块)
答:铺设这条人行道一共需要1000块红色地砖.
4.解:第一个图形可以摆棋子数:1×3=3个
第二个图形可以摆棋子数:2×4=8(个)
第三个图形可以摆棋子数:3×5=15(个)
……
第6个图形可以摆棋子数:
(6+2)×6
=8×6
=48(个)
……
第n个图形可以摆棋子数:(n+2)n个
答:第6个图形需要黑色棋子48个;则第n(n是大于0的整数)个图形需要黑色棋子(n+2)n个.
5.解:(1)由分析可知,第(5)个图形要用多少张小正方形卡纸是:
6+2×5
=6+10
=16(张)
答:第(5)个图形要用16张小正方形卡纸.
(2)由分析可知,第n个图形的周长是10+2n
因此,如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要(10+2n)厘米铁丝
答:至少需要(10+2n)厘米铁丝.
6.解:根据分析可得,
第n张餐桌,需要可坐(2+4n)人.
(1)2+4×4=18(人)
2+4×8=34(人)
答:若把4张这样的餐桌拼接起来,四周分别可坐
18人.若把8张这样的餐桌拼接起来,四周分别可坐
34人.
(2)2+4n=90
4n=88
n=22
答:若有餐的人数有90人,则这样的餐桌需要22张.
故答案为:18,34.
一.选择题
1.根据1÷11=0.
,2÷11=0.
,3÷11=0.
,可以推出9÷11=( )
A.0.
B.0.
C.0.
D.0.
2.如图是用棋子摆成的图形,摆第一个图形需要3枚棋子,摆第二个图形需要6枚棋子,摆第三个图形需要9枚棋子……照这样的规律摆第11个图形需要( )枚棋子.
A.27
B.30
C.33
D.36
3.寒假的时候,同学们去莲花山滑雪场滑雪,有些同学用雪杖摆成了如图:
像上面那样摆10个三角形,至少需要( )根滑雪杖.
A.21
B.20
C.9
D.30
4.用小棒摆正六边形,(如图所示),按照这样的方法摆下去,摆n个正六边形需要( )小棒.
A.6n
B.5n
C.5n+1
D.6n+1
5.如图的每个正方形中的四个数之间都有相同的规律,请根据此规律,计算出m的值是( )
A.86
B.74
C.52
6.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,n等于( )
A.52
B.74
C.86
二.填空题
1.按规律填数:
(1)2,4,6,8,
,12,
.
(2)56,46,36,26,
.
2.认真观察如图,看从中受到什么启发,然后再计算出后面算式的结果.
=
=
=
3.探索实践:如图,用“十字形”分割正方形.分割一次,可以分成4个正方形;分割二次,可以分成7个正方形……用这样的“十字形”连续分割3次,可以分成
个正方形;连续分割拟n次,可以分成
个正方形;要分成100个正方形需要分割
次.
4.观察如图的点阵图,找规律.
第五个点阵图有
点,第n个图形共有
个点.
5.找规律,填一填.
(1)1001、2002、3003、
、
、
.
(2)九千一百、八千二百、七千三百、
、
、
.
6.现有若干个圆环,它们的外直径都是5厘米,环宽5毫米,将它们扣在一起(如图所示)拉紧后测量总长度.
圆环个数
1
2
3
4
…
总长度(cm)
5
9
13
17
…
像这样,10个圆环拉紧后的长度是
厘米.如果圆环的个数为n,拉紧后总长度是
厘米.
三.判断题
1.用小棒照图搭正方形,搭一个正方形用4根,搭两个正方形用7根,搭a个正方形有4a根.(
)
2.按1、8、27、
、125、216的规律排,横线中的数应为64.(
)
3.第五个点阵中点的个数是:1+4×4=17.(
)
4.摆1个正方形需要4根小棒,往后每多摆1个正方形就增加3根小棒,按这样的规律摆10个正方形,一共需要31根小棒.(
)
5.如图:
那么第7个点阵有45个点.(
)
四.应用题
1.一张长方形桌子可坐6人,按下列方式将桌子拼在一起.
(1)2张桌子拼在一起可坐多少人?3张桌子拼在一起可坐多少人?
(2)一家餐厅有40张这样的长方形桌子,按照如图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)若在(2)中,改成每8张桌子拼成1张大桌子,则共可坐多少人?
2.小红用黑白两种方块照下图这样拼图.
(1)观察图形并填表.
图序
1
2
3
……
图中黑方块的个数
4
……
(2)思考问题并填空.
①图序为10的图中黑方块有
个;图序为n的图中黑方块有
个.
②小红拼成的一个图中白方块有26个,这个图的图序为
.
3.海安某步行街要铺设一条人行道,人行道长400米,宽1.6米.现在用边长都是0.4米的红、黄两种正方形地砖铺设(如图是铺设的局部图示).
(1)请帮忙算一算,铺设这条人行道一共需多少块地砖?(不计损耗)
(2)铺设这条人行道一共需要多少块红色地砖?(不计损耗)
4.如图,把同样大小的黑色棋子摆放在正多边形的边上,按这样的规律摆下去,第6个图形需要黑色棋子多少个?则第n(n是大于0的整数)个图形需要黑色棋子多少个?
5.小明用面积为1cm2的正方形卡纸拼摆图形.
(1)像这样拼下去,第(5)个图形要用多少张小正方形卡纸?
(2)如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要多少厘米铁丝?
6.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张这样的餐桌拼接起来,四周分别可坐
.
人:若把8张这样的餐桌拼接起来,四周分别可坐
人.
(2)若有餐的人数有90人,则这样的餐桌需要多少张?
答案
一.选择题
1.D.2.C.3.A.4.C.5.A.6.C.
二.填空题
1.10,14;16.
2.;;.
3.10;(3n+1);33.
4.18;3(n+1).
5.4004、5005、6006;六千四百、五千五百、四千六百.
6.41;(4n+1).
三.判断题
1.×.2.√.3.√.4.√.5.×.
四.应用题
1.解:(1)6+2=8(人)
6+2+2=10(人)
答:2张桌子拼在一起可坐8人;3张桌子拼在一起可坐10人.
(2)6+2+2+2+2=14(人)
8×14=112(人)
答:共可坐112人.
(3)6+2+2+2+2+2+2+2
=6+2×(8﹣1)
=6+14
=20(人)
40÷8×20
5×20
=100(人)
答:改成每8张桌子拼成1张大桌子,则共可坐100人.
2.解:(1)填表如下:
图序
1
2
3
……
图中黑方块的个数
4
6
8
……
(2)①图1黑色方块4个
图2黑色方块4+2=6(个)
图3黑色方块:4+2+2=8(个)
……
图10黑方块的个数:
2×10+2
=20+2
=22(个)
……
第n个图形黑色方块的个数为:4+2(n﹣1)=(2n+2)个
答:图序为10的图中黑方块有22个;图序为n的图中黑方块有(2n+2)个.
②白方块的排列规律为:
图1:5个
图2:5+3=9(个)
图3:5+3+3=11(个)
……
第n个图形白方块个数:5+3(n﹣1)=(3n+2)个
3n+2=26
3n=24
n=8
答:白方块有26个,这个图的图序为8.
故答案为:6,8;22,(2n+2);8.
3.解:(1)400×1.6÷0.42
=640÷0.16
=4000(块)
答:铺设这条人行道一共需4000块地砖.
(2)4000÷16×4
=250×4
=1000(块)
答:铺设这条人行道一共需要1000块红色地砖.
4.解:第一个图形可以摆棋子数:1×3=3个
第二个图形可以摆棋子数:2×4=8(个)
第三个图形可以摆棋子数:3×5=15(个)
……
第6个图形可以摆棋子数:
(6+2)×6
=8×6
=48(个)
……
第n个图形可以摆棋子数:(n+2)n个
答:第6个图形需要黑色棋子48个;则第n(n是大于0的整数)个图形需要黑色棋子(n+2)n个.
5.解:(1)由分析可知,第(5)个图形要用多少张小正方形卡纸是:
6+2×5
=6+10
=16(张)
答:第(5)个图形要用16张小正方形卡纸.
(2)由分析可知,第n个图形的周长是10+2n
因此,如果要在第n个图形的外围用铁丝镶上一圈边框,至少需要(10+2n)厘米铁丝
答:至少需要(10+2n)厘米铁丝.
6.解:根据分析可得,
第n张餐桌,需要可坐(2+4n)人.
(1)2+4×4=18(人)
2+4×8=34(人)
答:若把4张这样的餐桌拼接起来,四周分别可坐
18人.若把8张这样的餐桌拼接起来,四周分别可坐
34人.
(2)2+4n=90
4n=88
n=22
答:若有餐的人数有90人,则这样的餐桌需要22张.
故答案为:18,34.
