六年级下册数学一课一练-3.2圆锥 人教版(含答案)
文档属性
| 名称 | 六年级下册数学一课一练-3.2圆锥 人教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 37.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 00:00:00 | ||
图片预览


文档简介
六年级下册数学一课一练-3.2圆锥
一、单选题
1.一个圆锥和一个圆柱体积相等,底面积也相等,圆锥的高是12厘米,圆柱的高是(?? )厘米.
A.?4?????????????????????????????????????????????B.?12?????????????????????????????????????????????C.?36
2.一个圆柱与一个圆锥等底等高,它们的体积之和是60dm2 , 圆锥的体积是( ??)。
A.?15dm3???????????????????????????????B.?20dm3???????????????????????????????C.?30dm3???????????????????????????????D.?45dm3
3.1个圆柱形铁块可以浇铸成( ???)个与它等底等高的圆锥形铁块。
A.?1??????????????????????????????????????????????B.?2??????????????????????????????????????????????C.?3
4.一个圆锥的体积是100立方厘米,底面积是50平方厘米,它的高是(? ??)厘米。
A.?2??????????????????????????????????????????B.???????????????????????????????????????????C.?6??????????????????????????????????????????D.?10
二、判断题
5.两个等高的圆锥,底面半径的比为3:1,那么体积的比就是9:1。(??? )
6.从圆锥的顶点到底面圆周上任意一点的距离是圆锥的高。( ??)
7..圆锥的体积总是圆柱体积的 .(??? )
8.一个圆柱的体积是27m3 , 和它等底等高的圆锥的体积是9m3. (??? )
三、填空题
9.把圆柱的侧面沿高展开,得到的是一个________形;把圆锥的侧面展开,得到的是一个________形.
10.一个圆锥的体积是81立方厘米,底面积是27平方厘米,它的高是________厘米。
11.一个圆柱体和一个圆锥体的底面积相等,高的比是4∶3,体积比是________∶________。
12.一个底面半径是20cm、高是15cm的圆柱形铁块,可以熔铸成________个底面直径是20cm、高是15cm的圆锥形铁块。(损耗不计)
四、解答题
13.一个圆锥形的沙堆,底面积是31.4平方米,高3米。用这堆沙在10米宽的公路上铺0.02米厚的路面,可以铺多少米长?
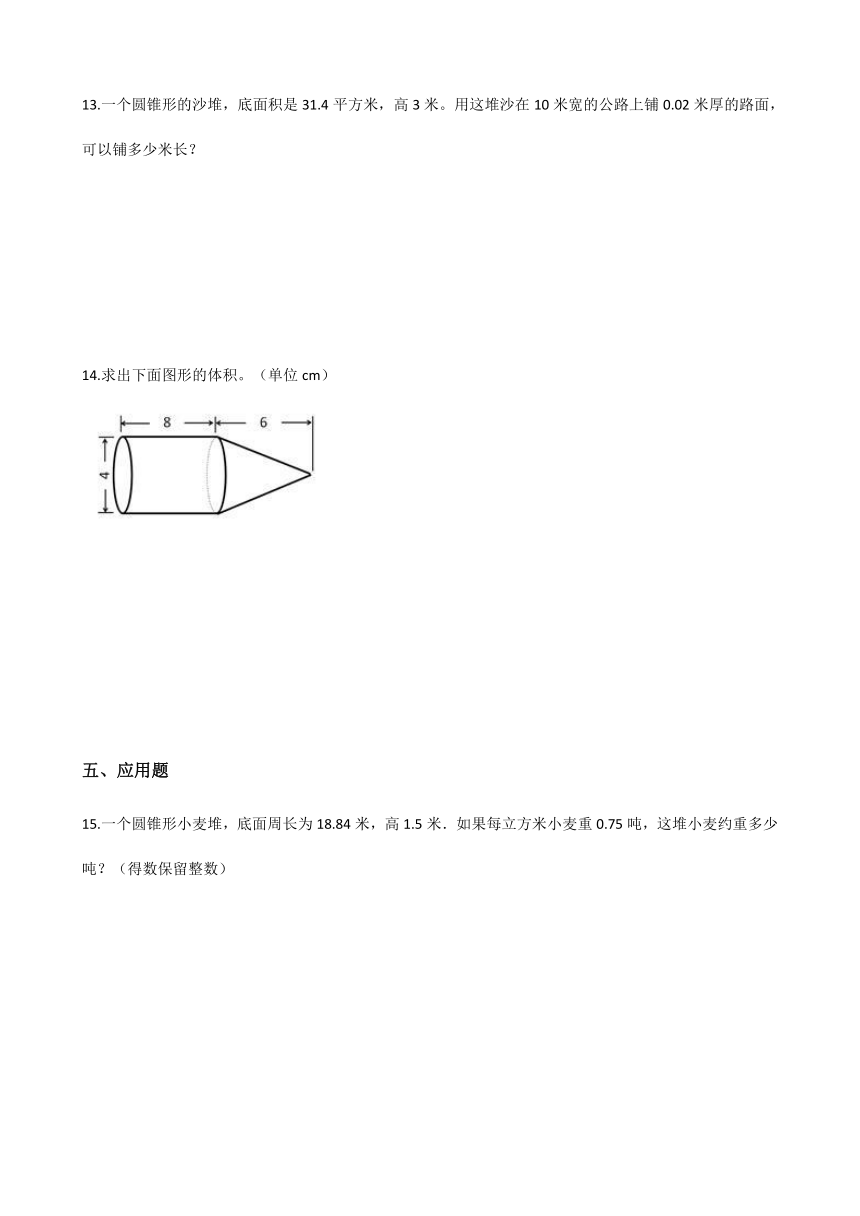
14.求出下面图形的体积。(单位cm)
五、应用题
15.一个圆锥形小麦堆,底面周长为18.84米,高1.5米.如果每立方米小麦重0.75吨,这堆小麦约重多少吨?(得数保留整数)
参考答案
一、单选题
1.【答案】 A
【解析】【解答】12÷3=4(厘米)
故答案为:A.
【分析】体积相等的圆柱和圆锥,当底面积相等时,圆锥的高是圆柱高的3倍,据此列式解答.
2.【答案】 A
【解析】【解答】解:60÷(3+1)
=60÷4
=15(dm?)
故答案为:A。
【分析】等底等高的圆柱体积是圆锥体积的3倍,圆锥的体积是1份,圆柱的体积就是3份。用体积和除以份数和即可求出1份是多少,也就是圆锥的体积。
3.【答案】 C
【解析】【解答】 1个圆柱形铁块可以浇铸成3个与它等底等高的圆锥形铁块。
故答案为:C。
【分析】等底等高,圆柱的体积是圆锥体积的3倍,故 1个圆柱形铁块可以浇铸成3个与它等底等高的圆锥形铁块。
4.【答案】 C
【解析】【解答】100×3÷50=300÷50=6(厘米)
故答案为:C。
【分析】圆锥的高=体积×3÷底面积。
二、判断题
5.【答案】正确
【解析】解答:两个等高的圆锥,底面半径的比为3:1,设 ,所以由体积公式可知,两者的体积之比为 。
分析:由圆锥的体积公式即可得。
6.【答案】 错误
【解析】【解答】解:从圆锥的顶点到底面圆心的距离是圆锥的高。原题说法错误。
故答案为:错误。
【分析】圆锥只有一条高,是圆锥顶点到底面圆心的距离。
7.【答案】 错误
【解析】【解答】圆锥的体积是等底等高的圆柱体积的.
故答案为:错误。
【分析】根据等底等高的圆锥体积与圆柱体积的关系:等底等高的圆柱体积是圆锥体积的3倍,据此解答即可。
8.【答案】 正确
【解析】【解答】解:27÷3=9(m?),原题说法正确.
故答案为:正确
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,所以等底等高的圆柱体积是圆锥体积的3倍,这样用圆柱的体积除以3即可求出和它等底等高的圆锥的体积.
三、填空题
9.【答案】 长方;扇
【解析】【解答】解:把圆柱的侧面沿高展开,得到的是一个长方形;把圆锥的侧面展开,得到的是一个扇形。
故答案为:长方;扇。
【分析】把圆柱的侧面沿着高剪开后会得到一个长方形或正方形,把圆锥的侧面展开,得到的是一个扇形。
10.【答案】 9
【解析】【解答】81×3÷27
=243÷27
=9(厘米)
故答案为:9.
【分析】根据圆锥的体积公式:V=Sh,已知圆锥的体积和底面积,求圆锥的高,用圆锥的体积×3÷圆锥的底面积=圆锥的高,据此列式解答.
11.【答案】4 ;1
【解析】【解答】解:假设底面积都是1,则体积比是:(1×4):(1×3×)=4:1.
故答案为:4;1
【分析】圆柱体积=底面积×高,圆锥体积=底面积×高×,假设底面积都是1,根据体积公式计算出体积,然后写出圆柱和圆锥的体积的最简整数比.
12.【答案】 12
【解析】【解答】解:20÷2=10(cm)
(3.14×20?×15)÷(3.14×10?×15×)
=(3.14×6000)÷(3.14×500)
=6000÷500
=12(个)
故答案为:12。
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×, 用圆柱的体积除以圆锥的体积即可求出熔铸乘圆锥的个数。
四、解答题
13.【答案】 解:×31.4×3
=×3×31.4
=1×31.4
=31.4(立方米)
31.4÷10÷0.02
=3.14÷0.02
=314÷2
=157(米)
答:可以铺157米路。
【解析】【分析】圆锥的体积=×底面积×高;长方体的体积=长×宽×高,长=长方体的体积÷宽÷高;代入数值计算即可。
14.【答案】 解:4÷2=2(cm)
3.14×22×8+3.14×22×6×
=3.14×4×8+3.14×4×6×
=100.48+25.12
=125.6(cm3)
【解析】【分析】观察图可知,这个组合图形是由一个圆柱和一个圆锥组合成的,圆柱和圆锥的底面积相等,圆柱的体积+圆锥的体积=组合图形的体积,据此列式解答。
五、应用题
15.【答案】 解:麦堆的体积:
×3.14×(18.84÷3.14÷2)2×1.5,
= ×3.14×32×1.5,
=3.14×9×0.5,
=14.13(立方米),麦的重量:
14.13×0.75≈11(吨);
答:这堆小麦约重11吨
【解析】【分析】要求这堆小麦的重量,先求得麦堆的体积,麦堆的形状是圆锥形的,利用圆锥的体积计算公式求得体积,进一步再求小麦的重量,问题得解.
一、单选题
1.一个圆锥和一个圆柱体积相等,底面积也相等,圆锥的高是12厘米,圆柱的高是(?? )厘米.
A.?4?????????????????????????????????????????????B.?12?????????????????????????????????????????????C.?36
2.一个圆柱与一个圆锥等底等高,它们的体积之和是60dm2 , 圆锥的体积是( ??)。
A.?15dm3???????????????????????????????B.?20dm3???????????????????????????????C.?30dm3???????????????????????????????D.?45dm3
3.1个圆柱形铁块可以浇铸成( ???)个与它等底等高的圆锥形铁块。
A.?1??????????????????????????????????????????????B.?2??????????????????????????????????????????????C.?3
4.一个圆锥的体积是100立方厘米,底面积是50平方厘米,它的高是(? ??)厘米。
A.?2??????????????????????????????????????????B.???????????????????????????????????????????C.?6??????????????????????????????????????????D.?10
二、判断题
5.两个等高的圆锥,底面半径的比为3:1,那么体积的比就是9:1。(??? )
6.从圆锥的顶点到底面圆周上任意一点的距离是圆锥的高。( ??)
7..圆锥的体积总是圆柱体积的 .(??? )
8.一个圆柱的体积是27m3 , 和它等底等高的圆锥的体积是9m3. (??? )
三、填空题
9.把圆柱的侧面沿高展开,得到的是一个________形;把圆锥的侧面展开,得到的是一个________形.
10.一个圆锥的体积是81立方厘米,底面积是27平方厘米,它的高是________厘米。
11.一个圆柱体和一个圆锥体的底面积相等,高的比是4∶3,体积比是________∶________。
12.一个底面半径是20cm、高是15cm的圆柱形铁块,可以熔铸成________个底面直径是20cm、高是15cm的圆锥形铁块。(损耗不计)
四、解答题
13.一个圆锥形的沙堆,底面积是31.4平方米,高3米。用这堆沙在10米宽的公路上铺0.02米厚的路面,可以铺多少米长?
14.求出下面图形的体积。(单位cm)
五、应用题
15.一个圆锥形小麦堆,底面周长为18.84米,高1.5米.如果每立方米小麦重0.75吨,这堆小麦约重多少吨?(得数保留整数)
参考答案
一、单选题
1.【答案】 A
【解析】【解答】12÷3=4(厘米)
故答案为:A.
【分析】体积相等的圆柱和圆锥,当底面积相等时,圆锥的高是圆柱高的3倍,据此列式解答.
2.【答案】 A
【解析】【解答】解:60÷(3+1)
=60÷4
=15(dm?)
故答案为:A。
【分析】等底等高的圆柱体积是圆锥体积的3倍,圆锥的体积是1份,圆柱的体积就是3份。用体积和除以份数和即可求出1份是多少,也就是圆锥的体积。
3.【答案】 C
【解析】【解答】 1个圆柱形铁块可以浇铸成3个与它等底等高的圆锥形铁块。
故答案为:C。
【分析】等底等高,圆柱的体积是圆锥体积的3倍,故 1个圆柱形铁块可以浇铸成3个与它等底等高的圆锥形铁块。
4.【答案】 C
【解析】【解答】100×3÷50=300÷50=6(厘米)
故答案为:C。
【分析】圆锥的高=体积×3÷底面积。
二、判断题
5.【答案】正确
【解析】解答:两个等高的圆锥,底面半径的比为3:1,设 ,所以由体积公式可知,两者的体积之比为 。
分析:由圆锥的体积公式即可得。
6.【答案】 错误
【解析】【解答】解:从圆锥的顶点到底面圆心的距离是圆锥的高。原题说法错误。
故答案为:错误。
【分析】圆锥只有一条高,是圆锥顶点到底面圆心的距离。
7.【答案】 错误
【解析】【解答】圆锥的体积是等底等高的圆柱体积的.
故答案为:错误。
【分析】根据等底等高的圆锥体积与圆柱体积的关系:等底等高的圆柱体积是圆锥体积的3倍,据此解答即可。
8.【答案】 正确
【解析】【解答】解:27÷3=9(m?),原题说法正确.
故答案为:正确
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,所以等底等高的圆柱体积是圆锥体积的3倍,这样用圆柱的体积除以3即可求出和它等底等高的圆锥的体积.
三、填空题
9.【答案】 长方;扇
【解析】【解答】解:把圆柱的侧面沿高展开,得到的是一个长方形;把圆锥的侧面展开,得到的是一个扇形。
故答案为:长方;扇。
【分析】把圆柱的侧面沿着高剪开后会得到一个长方形或正方形,把圆锥的侧面展开,得到的是一个扇形。
10.【答案】 9
【解析】【解答】81×3÷27
=243÷27
=9(厘米)
故答案为:9.
【分析】根据圆锥的体积公式:V=Sh,已知圆锥的体积和底面积,求圆锥的高,用圆锥的体积×3÷圆锥的底面积=圆锥的高,据此列式解答.
11.【答案】4 ;1
【解析】【解答】解:假设底面积都是1,则体积比是:(1×4):(1×3×)=4:1.
故答案为:4;1
【分析】圆柱体积=底面积×高,圆锥体积=底面积×高×,假设底面积都是1,根据体积公式计算出体积,然后写出圆柱和圆锥的体积的最简整数比.
12.【答案】 12
【解析】【解答】解:20÷2=10(cm)
(3.14×20?×15)÷(3.14×10?×15×)
=(3.14×6000)÷(3.14×500)
=6000÷500
=12(个)
故答案为:12。
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×, 用圆柱的体积除以圆锥的体积即可求出熔铸乘圆锥的个数。
四、解答题
13.【答案】 解:×31.4×3
=×3×31.4
=1×31.4
=31.4(立方米)
31.4÷10÷0.02
=3.14÷0.02
=314÷2
=157(米)
答:可以铺157米路。
【解析】【分析】圆锥的体积=×底面积×高;长方体的体积=长×宽×高,长=长方体的体积÷宽÷高;代入数值计算即可。
14.【答案】 解:4÷2=2(cm)
3.14×22×8+3.14×22×6×
=3.14×4×8+3.14×4×6×
=100.48+25.12
=125.6(cm3)
【解析】【分析】观察图可知,这个组合图形是由一个圆柱和一个圆锥组合成的,圆柱和圆锥的底面积相等,圆柱的体积+圆锥的体积=组合图形的体积,据此列式解答。
五、应用题
15.【答案】 解:麦堆的体积:
×3.14×(18.84÷3.14÷2)2×1.5,
= ×3.14×32×1.5,
=3.14×9×0.5,
=14.13(立方米),麦的重量:
14.13×0.75≈11(吨);
答:这堆小麦约重11吨
【解析】【分析】要求这堆小麦的重量,先求得麦堆的体积,麦堆的形状是圆锥形的,利用圆锥的体积计算公式求得体积,进一步再求小麦的重量,问题得解.
