28.2.2直线与圆的位置关系课件
文档属性
| 名称 | 28.2.2直线与圆的位置关系课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 173.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-29 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
学习目标:
1、理解直线和圆的三种位置关系。
2、掌握判定直线和圆的位置关系的方法,能判断
简单的位置关系。
重点、难点:
利用圆心到直线的距离与半径的关系判别直线 与圆的位置关系。
海上升明月 天涯共此时
●O
●O
●O
思考:直线与圆有几种位置关系
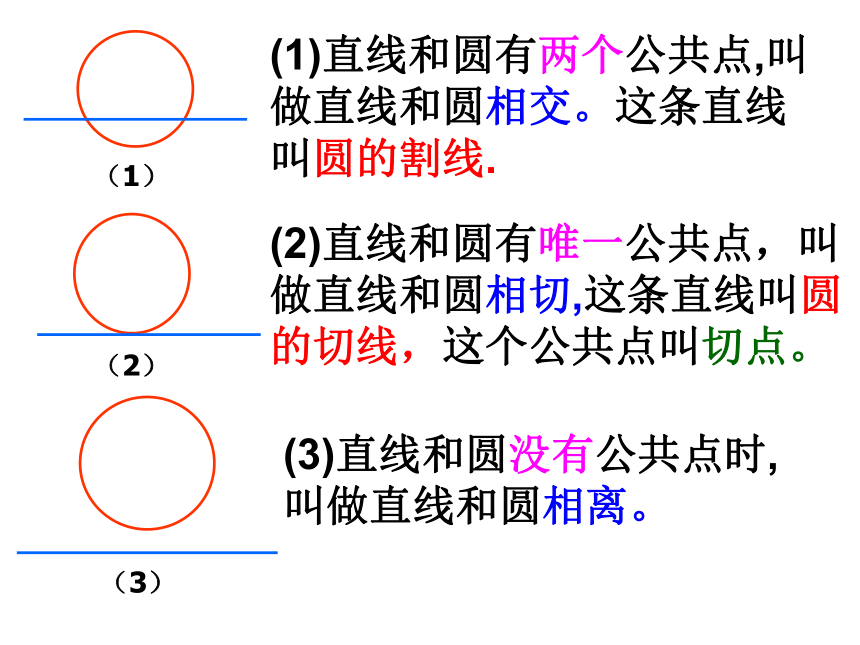
(2)直线和圆有唯一公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点。
(1)直线和圆有两个公共点,叫做直线和圆相交。这条直线叫圆的割线.
(3)直线和圆没有公共点时,叫做直线和圆相离。
(1)
(2)
(3)
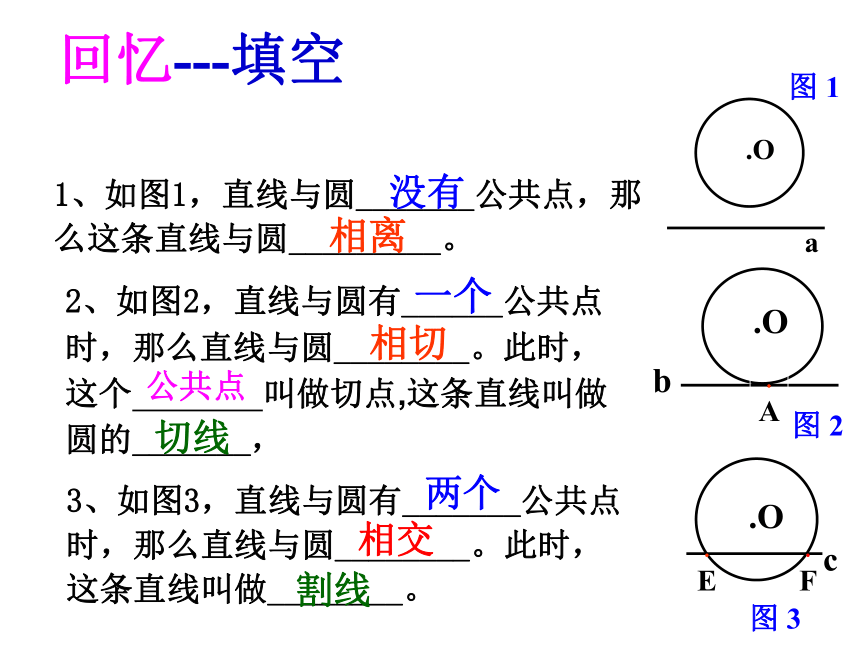
回忆---填空
图 1
b
.
A
.O
图 2
c
.
F
.E
.O
图 3
2、如图2,直线与圆有______公共点时,那么直线与圆________。此时,这个 叫做切点,这条直线叫做圆的_______,
相切
相离
.O
a
1、如图1,直线与圆_______公共点,那么这条直线与圆_________。
没有
一个
3、如图3,直线与圆有_______公共点时,那么直线与圆________。此时,这条直线叫做________。
切线
两个
相交
割线
公共点
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
l
l
l
.A
.B
.
C
.D
.E
.F
. N
H
Q
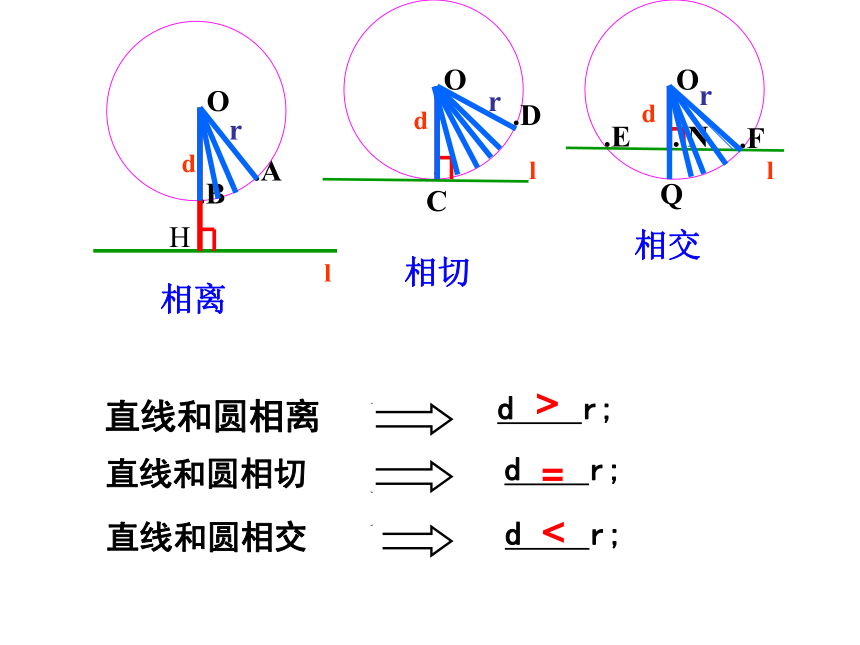
直线和圆相离
d r;
d r;
直线和圆相切
直线和圆相交
d r;
<
=
>
直线和圆相离
d = r
d > r
直线和圆相切
直线和圆相交
d < r
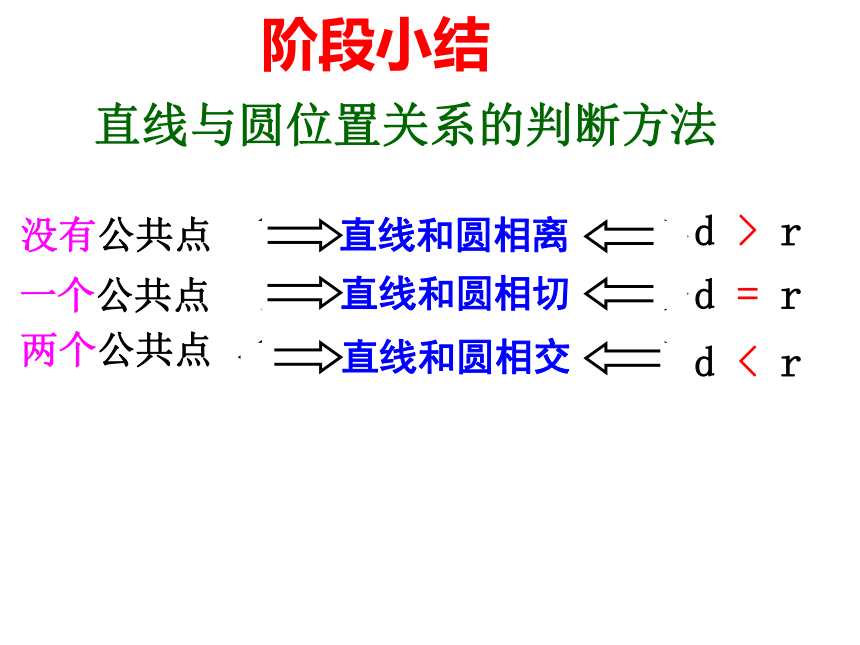
没有公共点
一个公共点
两个公共点
直线与圆位置关系的判断方法
阶段小结
基础练习1
1、直线与圆最多有两个公共点 。… ( )
√
×
判断
3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( )
.A
.O
2、若直线与圆相交,则直线上的点都在圆内。( )
4 、若C为⊙O外的一点,则过点C的直线CD与
⊙O 相交或相离。………( )
×
×
.C
例题:
在Rt△ABC中,∠C为90度,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm (2)r=2.4cm (3)r=3cm
B
C A
解:过C作CD⊥AB,垂足为D
D
在Rt△ABC中,
AB=
5
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm
(1)当r=2cm时,
有d>r,
因此⊙C和AB相离。
B
C A
(2)当r=2.4cm时,
有d=r,
因此⊙C和AB相切。
B
C
B
C A
(3)当r=3cm时,
有d因此,⊙C和AB相交。
D
D
1.已知圆的半径为5cm,如果直线和圆心的距离为:
(1)4cm (2)5cm (3)6cm
那么直线和圆有几个公共点?它与圆成何种位置关系?
基础练习2
2.如图,已知∠ AOB=30° ,M为OB上一点,且OM=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?
(1) r = 2cm
(2) r = 4cm
(3) r = 2.5cm
M
O
A
B
C
基础练习3
填空:
1、已知⊙O的半径为5cm,点O到直线a的距离为5cm,则⊙O与直线a的位置关系是_____;直线a与⊙O的公共点个数是____.
相切
2、已知⊙O的直径为10cm,直线a与⊙O只有一个公共点,则圆心到直线a的距离是____。
一个
3、圆心O到直线m上一点A的距离等于⊙O的
半径,则直线m与⊙O的位置关系是 。
相切
5cm
随堂检测
1. ⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
2.直线上一点到圆心O的距离等于⊙O的半径,则直线和⊙O的位置 关系是( )
A.相离 B.相交 C.相切 D.相切或相交
判断: 若线段和圆没有公共点,该圆圆心到线段的距离大于半径. ( )
请做随堂练习!
A
D
×
4.判断:若直线和圆相切,则该直线和圆一定有一个公共点. ( )
√
5、在等腰△ABC中,AB=AC=2cm,若以A为圆心,1cm为半径的圆与BC相切,则∠BAC的度数为多少?( )
A、30°B、60°C、90°D、120°
A
C
B
2
2
D
解:过A点作AD⊥BC于D,
∵⊙O与BC相切, AD⊥BC
∴AD= ⊙O的半径 =1cm,
在RtABD中,∠ADB=90°
∵BC=1/2 AD,
∴∠ABC=30°,∠BAC=120°
D
在等腰△ABC中,AB=AC=2,⊙A的半径为1
(1)当∠BAC满足 时,
直线AB与⊙A相交;
(2)当∠BAC满足 时,
直线AB与⊙A相离。
C
B
A
变式练习
C
B
A
120°< ∠BAC<180°
0°< ∠BAC<120°
为什么车轮做成圆的?
课堂小结:直线与圆的位置关系
0
d>r
1
d=r
切点
切线
2
d.O
d
r
┐
┐
.o
d
r
.O
d
┐
r
.
P
C
B
.
相离
相切
相交
A
割线
交点
课下作业
课本: P54(第5、6题)
学习目标:
1、理解直线和圆的三种位置关系。
2、掌握判定直线和圆的位置关系的方法,能判断
简单的位置关系。
重点、难点:
利用圆心到直线的距离与半径的关系判别直线 与圆的位置关系。
海上升明月 天涯共此时
●O
●O
●O
思考:直线与圆有几种位置关系
(2)直线和圆有唯一公共点,叫做直线和圆相切,这条直线叫圆的切线,这个公共点叫切点。
(1)直线和圆有两个公共点,叫做直线和圆相交。这条直线叫圆的割线.
(3)直线和圆没有公共点时,叫做直线和圆相离。
(1)
(2)
(3)
回忆---填空
图 1
b
.
A
.O
图 2
c
.
F
.E
.O
图 3
2、如图2,直线与圆有______公共点时,那么直线与圆________。此时,这个 叫做切点,这条直线叫做圆的_______,
相切
相离
.O
a
1、如图1,直线与圆_______公共点,那么这条直线与圆_________。
没有
一个
3、如图3,直线与圆有_______公共点时,那么直线与圆________。此时,这条直线叫做________。
切线
两个
相交
割线
公共点
d
d
d
.O
.O
.O
r
r
r
相离
相切
相交
l
l
l
.A
.B
.
C
.D
.E
.F
. N
H
Q
直线和圆相离
d r;
d r;
直线和圆相切
直线和圆相交
d r;
<
=
>
直线和圆相离
d = r
d > r
直线和圆相切
直线和圆相交
d < r
没有公共点
一个公共点
两个公共点
直线与圆位置关系的判断方法
阶段小结
基础练习1
1、直线与圆最多有两个公共点 。… ( )
√
×
判断
3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( )
.A
.O
2、若直线与圆相交,则直线上的点都在圆内。( )
4 、若C为⊙O外的一点,则过点C的直线CD与
⊙O 相交或相离。………( )
×
×
.C
例题:
在Rt△ABC中,∠C为90度,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm (2)r=2.4cm (3)r=3cm
B
C A
解:过C作CD⊥AB,垂足为D
D
在Rt△ABC中,
AB=
5
根据三角形的面积公式有
∴
即圆心C到AB的距离d=2.4cm
(1)当r=2cm时,
有d>r,
因此⊙C和AB相离。
B
C A
(2)当r=2.4cm时,
有d=r,
因此⊙C和AB相切。
B
C
B
C A
(3)当r=3cm时,
有d
D
D
1.已知圆的半径为5cm,如果直线和圆心的距离为:
(1)4cm (2)5cm (3)6cm
那么直线和圆有几个公共点?它与圆成何种位置关系?
基础练习2
2.如图,已知∠ AOB=30° ,M为OB上一点,且OM=5cm,以M为圆心,以r为半径的圆与直线OA有怎样的位置关系?为什么?
(1) r = 2cm
(2) r = 4cm
(3) r = 2.5cm
M
O
A
B
C
基础练习3
填空:
1、已知⊙O的半径为5cm,点O到直线a的距离为5cm,则⊙O与直线a的位置关系是_____;直线a与⊙O的公共点个数是____.
相切
2、已知⊙O的直径为10cm,直线a与⊙O只有一个公共点,则圆心到直线a的距离是____。
一个
3、圆心O到直线m上一点A的距离等于⊙O的
半径,则直线m与⊙O的位置关系是 。
相切
5cm
随堂检测
1. ⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( )
A.d >3 B.d<3 C.d ≤3 D.d =3
2.直线上一点到圆心O的距离等于⊙O的半径,则直线和⊙O的位置 关系是( )
A.相离 B.相交 C.相切 D.相切或相交
判断: 若线段和圆没有公共点,该圆圆心到线段的距离大于半径. ( )
请做随堂练习!
A
D
×
4.判断:若直线和圆相切,则该直线和圆一定有一个公共点. ( )
√
5、在等腰△ABC中,AB=AC=2cm,若以A为圆心,1cm为半径的圆与BC相切,则∠BAC的度数为多少?( )
A、30°B、60°C、90°D、120°
A
C
B
2
2
D
解:过A点作AD⊥BC于D,
∵⊙O与BC相切, AD⊥BC
∴AD= ⊙O的半径 =1cm,
在RtABD中,∠ADB=90°
∵BC=1/2 AD,
∴∠ABC=30°,∠BAC=120°
D
在等腰△ABC中,AB=AC=2,⊙A的半径为1
(1)当∠BAC满足 时,
直线AB与⊙A相交;
(2)当∠BAC满足 时,
直线AB与⊙A相离。
C
B
A
变式练习
C
B
A
120°< ∠BAC<180°
0°< ∠BAC<120°
为什么车轮做成圆的?
课堂小结:直线与圆的位置关系
0
d>r
1
d=r
切点
切线
2
d
d
r
┐
┐
.o
d
r
.O
d
┐
r
.
P
C
B
.
相离
相切
相交
A
割线
交点
课下作业
课本: P54(第5、6题)
