2020——2021 苏科版数学九年级下册:第7章 锐角函数 综合测试 (word版含答案)
文档属性
| 名称 | 2020——2021 苏科版数学九年级下册:第7章 锐角函数 综合测试 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 779.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 14:26:18 | ||
图片预览


文档简介
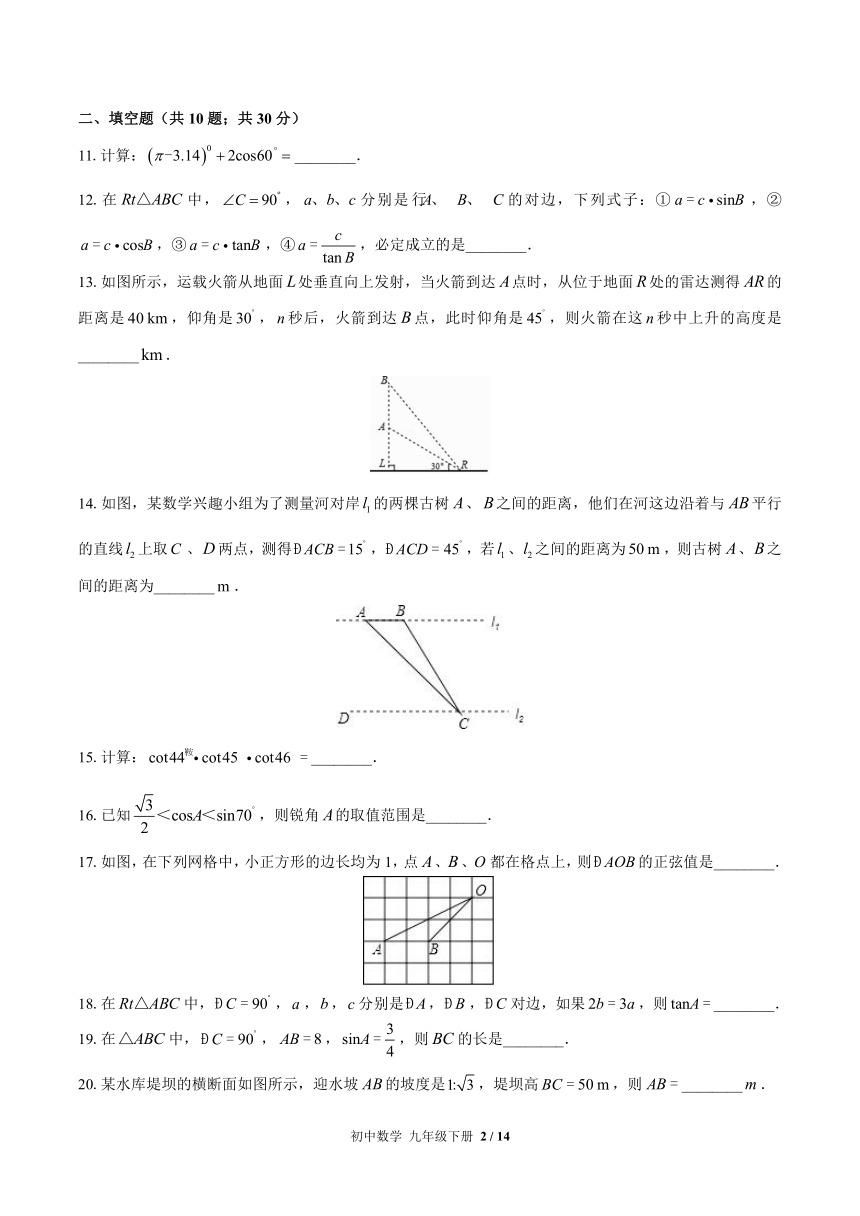
第7章综合测试
一、单选题(共10题;共30分)
1.在false中,false,false,false,那么下面各式正确的是( )
A.false B.false C.false D.false
2.在false中,false,false,false,则false的值是( )
A.false B.false C.false D.false
3.false的值为( )
A.false B.false C.false D.false
4.三角形在方格纸中的位置如图所示,则false的值是( )
A.false B.false C.false D.false
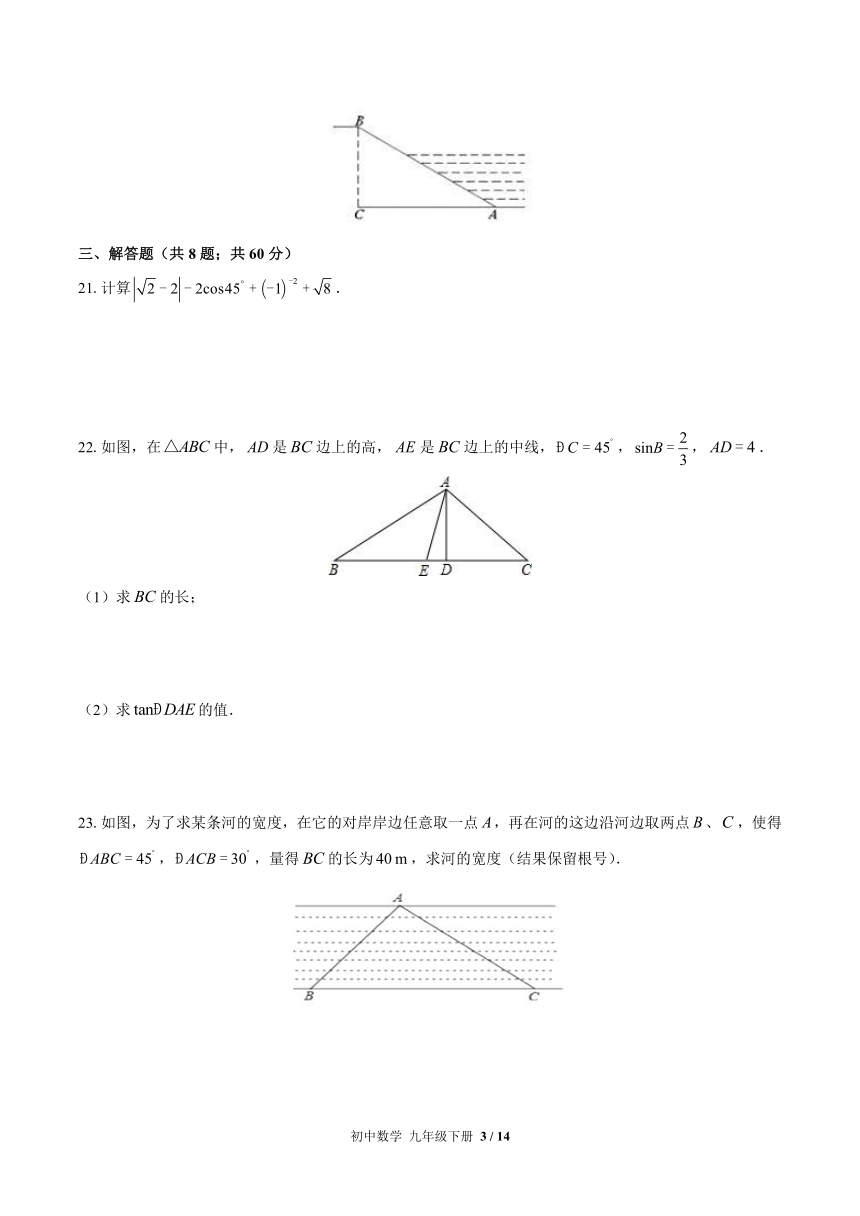
5.已知在false中,false,false,false,则下列结论正确的是( )
A.false B.false C.false D.false
6.在false中,已知false,false,false,那么false的余弦值等于( )
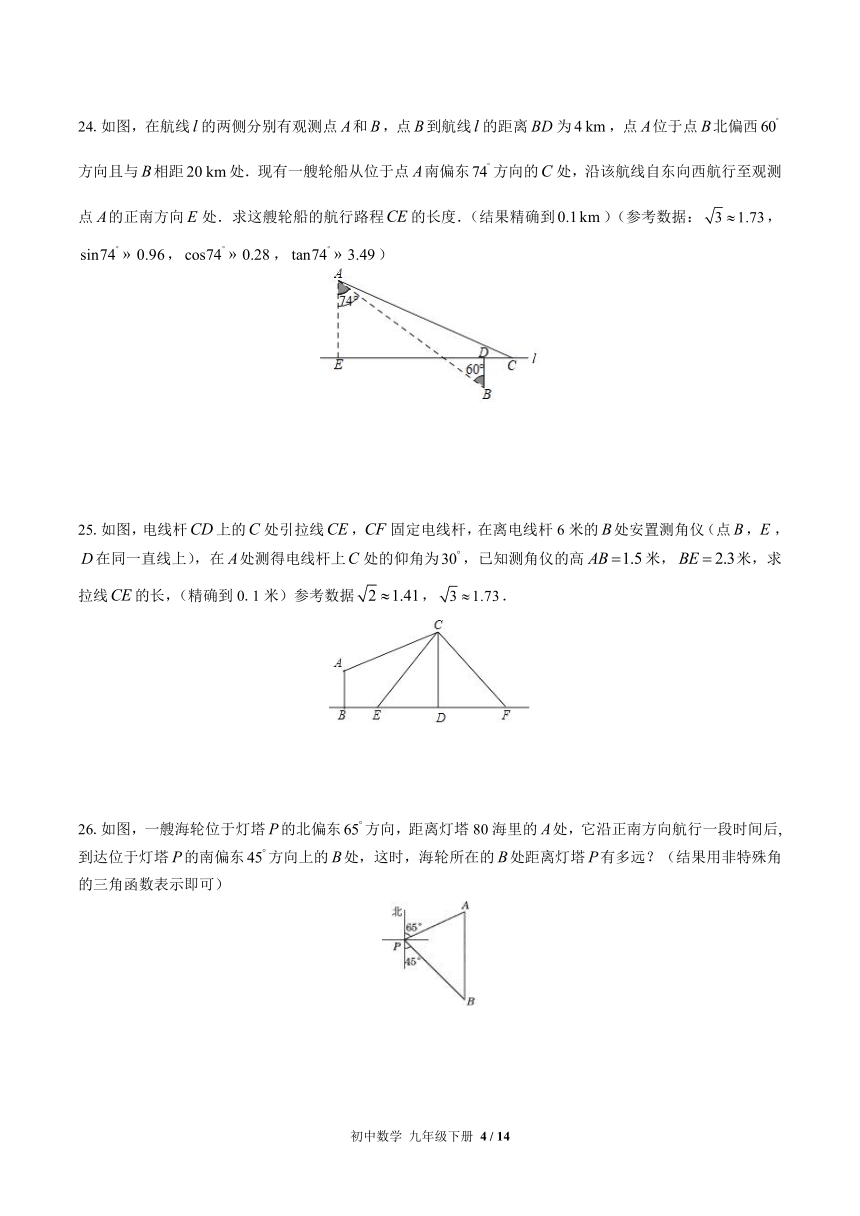
A.false B.false C.false D.false
7.在false中,false,false,则false等于( )
A.false B.false C.false D.false
8.在false中,false,false,false,则false( )
A.false B.false C.false D.false
9.在false中,若false,则false的度数是( )
A.false B.false C.false D.false
10.一个人从山下沿false角的坡路登上山顶,共走了false,那么这山的高度是( )false
A.230 B.240 C.250 D.260
二、填空题(共10题;共30分)
11.计算:false________.
12.在false中,false,false分别是false的对边,下列式子:①false,②false,③false,④false,必定成立的是________.
13.如图所示,运载火箭从地面false处垂直向上发射,当火箭到达false点时,从位于地面false处的雷达测得false的距离是false,仰角是false,false秒后,火箭到达false点,此时仰角是false,则火箭在这false秒中上升的高度是________false.
14.如图,某数学兴趣小组为了测量河对岸false的两棵古树false、false之间的距离,他们在河这边沿着与false平行的直线false上取false、false两点,测得false,false,若false、false之间的距离为false,则古树false、false之间的距离为________false.
15.计算:false________.
16.已知false,则锐角false的取值范围是________.
17.如图,在下列网格中,小正方形的边长均为1,点false、false、false都在格点上,则false的正弦值是________.
18.在false中,false,false,false,false分别是false,false,false对边,如果false,则false________.
19.在false中,false,false,false,则false的长是________.
20.某水库堤坝的横断面如图所示,迎水坡false的坡度是false,堤坝高false,则false________false.
三、解答题(共8题;共60分)
21.计算false.
22.如图,在false中,false是false边上的高,false是false边上的中线,false,false,false.
(1)求false的长;
(2)求false的值.
23.如图,为了求某条河的宽度,在它的对岸岸边任意取一点false,再在河的这边沿河边取两点false、false,使得false,false,量得false的长为false,求河的宽度(结果保留根号).
24.如图,在航线false的两侧分别有观测点false和false,点false到航线false的距离false为false,点false位于点false北偏西false方向且与false相距false处.现有一艘轮船从位于点false南偏东false方向的false处,沿该航线自东向西航行至观测点false的正南方向false处.求这艘轮船的航行路程false的长度.(结果精确到false)(参考数据:false,false,false,false)
25.如图,电线杆false上的false处引拉线false,false固定电线杆,在离电线杆6米的false处安置测角仪(点false,false,false在同一直线上),在false处测得电线杆上false处的仰角为false,已知测角仪的高false米,false米,求拉线false的长,(精确到0.1米)参考数据false,false.
26.如图,一艘海轮位于灯塔false的北偏东false方向,距离灯塔80海里的false处,它沿正南方向航行一段时间后,到达位于灯塔false的南偏东false方向上的false处,这时,海轮所在的false处距离灯塔false有多远?(结果用非特殊角的三角函数表示即可)
27.如图所示,某小组同学为了测量对面楼false的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为false,底端B的俯角为false,请你根据以上数据,求出楼false的高度.(精确到0.1米)
(参考数据:false,false,false,false,false)
28.某市在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌false(如图所示),已知立杆false的高度是3米,从侧面false点测到路况警示牌顶端false点和底端false点的仰角分别是false和false,求路况警示牌宽false的值.
第7章综合测试
答案解析
一、
1.【答案】C
【解析】本题可以利用锐角三角函数的定义求解.
因为:false,所以false.
故选C.
【考点】锐角三角函数的定义
2.【答案】B
【解析】根据题意画出图形,由勾股定理求出false的长,再由锐角三角函数的定义进行解答即可.
如图所示:
false中,false,false,false,
false,
false.
故答案为:B.
【考点】锐角三角函数的定义
3.【答案】C
【解析】解:false.故答案为:C.
根据特殊锐角的三角函数值即可得出答案.
【考点】特殊角的三角函数值
4.【答案】A
【解析】根据三角函数的定义就可以解决.
在直角三角形中,正切值等于对边比上邻边,
false.
故选A.
【考点】锐角三角函数的定义
5.【答案】C
【解析】根据锐角三角函数的定义,对各选项进行判断即可.
由题意得:false,
A、false,故本选项错误;
B、false,故本选项错误;
C、false,故本选项正确;
D、false,故本选项错误.
故选C.
【考点】锐角三角函数的定义
6.【答案】A
【解析】解:在false中,false,false,false,
false,
false.
故选A.
【考点】锐角三角函数的定义
7.【答案】C
【解析】解:false,false,false,得false,所以false.
故答案选:C.
【考点】互余两角三角函数的关系
8.【答案】C
【解析】直接根据余弦的定义即可得到答案.
false中,false,,false,false,
false.
故选C.
【考点】锐角三角函数的定义
9.【答案】C
【解析】解:false中,false
false,false.
false,false.false.
故选C.
【考点】特殊角的三角函数值
10.【答案】C
【解析】由false所对的直角边是斜边的一半,得此山的高度false.
故选C.
【考点】解直角三角形的应用—坡度坡角问题
二、
11.【答案】2
【解析】根据0指数的意义,特殊锐角三角函数值分别化简,再按有理数的混合运算顺序算出答案.
原式false.
故答案为:2.
【考点】实数的运算,特殊角的三角函数值
12.【答案】②
【解析】根据锐角三角函数的意义可判断正误.
解:∵在false中,false,false分别是false的对边,
false,
false,故①错误;
false,
false,故②正确;
false,
false,故③错误;
false,
false,故④错误.
故答案为②.
【考点】锐角三角函数的定义
13.【答案】false
【解析】解:在false中,
false,
在false中,false,
false,
false,
故答案为false.
【考点】解直角三角形的应用
14.【答案】false
【解析】解:如图,过点false作false于点false,过点false作false于点false.则false,false.
在直角false,false,false,
false.
false在直角false中,false,false,
false,
false.
则false.
故答案是:false.
【考点】解直角三角形的应用
15.【答案】1
【解析】根据互余两角的三角函数的关系、特殊角的三角函数值就可以求解.
解:false.
【考点】特殊角的三角函数值
16.【答案】false
【解析】利用特殊角的三角函数值以及互余两角的锐角三角函数关系得出false的取值范围.
解:false,
false,
false.
故答案为:false.
【考点】锐角三角函数的增减性
17.【答案】false
【解析】利用勾股定理求出false的长,再由false可得答案.
解:由题意可知,false,false,false,false,
false,
false,
故答案为:false.
【考点】锐角三角函数的定义
18.【答案】false
【解析】根据锐角三角函数的定义可得false,然后根据题目所给false可求解.
解:false,false分别是false对边,false,false,false,false.
故答案为:false.
【考点】锐角三角函数的定义
19.【答案】6
【解析】根据三角函数值直接求出false的长即可.
false,
false,解得false.
【考点】锐角三角函数的定义
20.【答案】100
【解析】由坡度的意义可得出两直角边的关系,进而求出斜边.
根据坡度可得:false,根据false,则false.
【考点】解直角三角形的应用—坡度坡角问题
三、
21.【答案】解:原式false.
【解析】根据二次根式,负指数幂,绝对值,特殊角的三角函数值等性质计算即可得出答案.
【考点】实数的运算,负整数指数幂的运算性质,二次根式的性质与化简,特殊角的三角函数值,实数的绝对值
22.【答案】(1)在false中,false是false边上的高,
false.
在false中,false,false,false,
false.
在false中,false,false,false,
false.
false.
false.
(2)false是false边上的中线,
false,
false,
false.
【解析】解直角三角形
(1)先由三角形的高的定义得出false,再解false,得出false;解false,得出false,根据勾股定理求出false,然后根据false即可求解;
(2)先由三角形的中线的定义求出false的值,则false,然后在false中根据正切函数的定义即可求解.
【考点】解直角三角形
23.【答案】解:作false,垂足为false.
设false,
false,
false,
false,
false,
false,且false,
false,
解得,false,
答:则河的宽度为false
【解析】作false,垂足为false.利用解直角三角形的知识进行求解即可.
【考点】解直角三角形的应用
24.【答案】解:如图,
在false中,false,
false,
false,
false,
false,false,
false,
false,
false,
在false中,false.
故这艘轮船的航行路程false的长度是false.
【解析】首先在false中,根据特殊锐角三角函数值和三角函数的定义可求得false的长,进一步求出false,然后,再证明false,依据相似三角形的性质可求得false的长,最后,在false中根据三角函数可求这艘轮船的航行路程false的长度.
【考点】解直角三角形的应用—仰角俯角问题
25.【答案】解:过点false作false于点false,则四边形false为矩形,false,
在false中,false,false,
false,
false,
在false中,false,
false.
【解析】过点false作false于点false,可得四边形false为矩形,根据false处测得电线杆上false处得仰角为false,在false中求出false的长度,然后在false中求出false的长度.
【考点】矩形的性质,解直角三角形的应用—仰角俯角问题
26.【答案】解:如图,过点false作false于点false.
由题意知false.
在false中,false,false.
false点false在点false的北偏东false方向上,false.
在false中,false.
false,
false
【解析】过点false作false于点false,根据方位角,在false中,求出false;然后在false中,求出false.
【考点】解直角三角形的应用—方向角问题
27.【答案】解:过点false作false于点false,
在false中,false,false,false,
false.
在false中,false,false,false,
false
false.
【解析】根据已知底端B的俯角为false,添加辅助线过点false作false于点false,先在false中,利用锐角三角函数的定义求出false的长,再在false中,利用false的正切求出false的长,然后根据false,求出false的长即可.
【考点】锐角三角函数的定义,特殊角的三角函数值,解直角三角形的应用—仰角俯角问题
28.【答案】解:false在false中,false,false,
false,
在false中,false,
false,
false.
false.
答:路况显示牌false是false
【解析】在false中,知道了已知角的对边,可用正切函数求出邻边false的长;同理在false中,知道了已知角的邻边,用正切值即可求出对边false的长;进而由false得解.
【考点】解直角三角形的应用
一、单选题(共10题;共30分)
1.在false中,false,false,false,那么下面各式正确的是( )
A.false B.false C.false D.false
2.在false中,false,false,false,则false的值是( )
A.false B.false C.false D.false
3.false的值为( )
A.false B.false C.false D.false
4.三角形在方格纸中的位置如图所示,则false的值是( )
A.false B.false C.false D.false
5.已知在false中,false,false,false,则下列结论正确的是( )
A.false B.false C.false D.false
6.在false中,已知false,false,false,那么false的余弦值等于( )
A.false B.false C.false D.false
7.在false中,false,false,则false等于( )
A.false B.false C.false D.false
8.在false中,false,false,false,则false( )
A.false B.false C.false D.false
9.在false中,若false,则false的度数是( )
A.false B.false C.false D.false
10.一个人从山下沿false角的坡路登上山顶,共走了false,那么这山的高度是( )false
A.230 B.240 C.250 D.260
二、填空题(共10题;共30分)
11.计算:false________.
12.在false中,false,false分别是false的对边,下列式子:①false,②false,③false,④false,必定成立的是________.
13.如图所示,运载火箭从地面false处垂直向上发射,当火箭到达false点时,从位于地面false处的雷达测得false的距离是false,仰角是false,false秒后,火箭到达false点,此时仰角是false,则火箭在这false秒中上升的高度是________false.
14.如图,某数学兴趣小组为了测量河对岸false的两棵古树false、false之间的距离,他们在河这边沿着与false平行的直线false上取false、false两点,测得false,false,若false、false之间的距离为false,则古树false、false之间的距离为________false.
15.计算:false________.
16.已知false,则锐角false的取值范围是________.
17.如图,在下列网格中,小正方形的边长均为1,点false、false、false都在格点上,则false的正弦值是________.
18.在false中,false,false,false,false分别是false,false,false对边,如果false,则false________.
19.在false中,false,false,false,则false的长是________.
20.某水库堤坝的横断面如图所示,迎水坡false的坡度是false,堤坝高false,则false________false.
三、解答题(共8题;共60分)
21.计算false.
22.如图,在false中,false是false边上的高,false是false边上的中线,false,false,false.
(1)求false的长;
(2)求false的值.
23.如图,为了求某条河的宽度,在它的对岸岸边任意取一点false,再在河的这边沿河边取两点false、false,使得false,false,量得false的长为false,求河的宽度(结果保留根号).
24.如图,在航线false的两侧分别有观测点false和false,点false到航线false的距离false为false,点false位于点false北偏西false方向且与false相距false处.现有一艘轮船从位于点false南偏东false方向的false处,沿该航线自东向西航行至观测点false的正南方向false处.求这艘轮船的航行路程false的长度.(结果精确到false)(参考数据:false,false,false,false)
25.如图,电线杆false上的false处引拉线false,false固定电线杆,在离电线杆6米的false处安置测角仪(点false,false,false在同一直线上),在false处测得电线杆上false处的仰角为false,已知测角仪的高false米,false米,求拉线false的长,(精确到0.1米)参考数据false,false.
26.如图,一艘海轮位于灯塔false的北偏东false方向,距离灯塔80海里的false处,它沿正南方向航行一段时间后,到达位于灯塔false的南偏东false方向上的false处,这时,海轮所在的false处距离灯塔false有多远?(结果用非特殊角的三角函数表示即可)
27.如图所示,某小组同学为了测量对面楼false的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为false,底端B的俯角为false,请你根据以上数据,求出楼false的高度.(精确到0.1米)
(参考数据:false,false,false,false,false)
28.某市在地铁施工期间,交管部门在施工路段设立了矩形路况警示牌false(如图所示),已知立杆false的高度是3米,从侧面false点测到路况警示牌顶端false点和底端false点的仰角分别是false和false,求路况警示牌宽false的值.
第7章综合测试
答案解析
一、
1.【答案】C
【解析】本题可以利用锐角三角函数的定义求解.
因为:false,所以false.
故选C.
【考点】锐角三角函数的定义
2.【答案】B
【解析】根据题意画出图形,由勾股定理求出false的长,再由锐角三角函数的定义进行解答即可.
如图所示:
false中,false,false,false,
false,
false.
故答案为:B.
【考点】锐角三角函数的定义
3.【答案】C
【解析】解:false.故答案为:C.
根据特殊锐角的三角函数值即可得出答案.
【考点】特殊角的三角函数值
4.【答案】A
【解析】根据三角函数的定义就可以解决.
在直角三角形中,正切值等于对边比上邻边,
false.
故选A.
【考点】锐角三角函数的定义
5.【答案】C
【解析】根据锐角三角函数的定义,对各选项进行判断即可.
由题意得:false,
A、false,故本选项错误;
B、false,故本选项错误;
C、false,故本选项正确;
D、false,故本选项错误.
故选C.
【考点】锐角三角函数的定义
6.【答案】A
【解析】解:在false中,false,false,false,
false,
false.
故选A.
【考点】锐角三角函数的定义
7.【答案】C
【解析】解:false,false,false,得false,所以false.
故答案选:C.
【考点】互余两角三角函数的关系
8.【答案】C
【解析】直接根据余弦的定义即可得到答案.
false中,false,,false,false,
false.
故选C.
【考点】锐角三角函数的定义
9.【答案】C
【解析】解:false中,false
false,false.
false,false.false.
故选C.
【考点】特殊角的三角函数值
10.【答案】C
【解析】由false所对的直角边是斜边的一半,得此山的高度false.
故选C.
【考点】解直角三角形的应用—坡度坡角问题
二、
11.【答案】2
【解析】根据0指数的意义,特殊锐角三角函数值分别化简,再按有理数的混合运算顺序算出答案.
原式false.
故答案为:2.
【考点】实数的运算,特殊角的三角函数值
12.【答案】②
【解析】根据锐角三角函数的意义可判断正误.
解:∵在false中,false,false分别是false的对边,
false,
false,故①错误;
false,
false,故②正确;
false,
false,故③错误;
false,
false,故④错误.
故答案为②.
【考点】锐角三角函数的定义
13.【答案】false
【解析】解:在false中,
false,
在false中,false,
false,
false,
故答案为false.
【考点】解直角三角形的应用
14.【答案】false
【解析】解:如图,过点false作false于点false,过点false作false于点false.则false,false.
在直角false,false,false,
false.
false在直角false中,false,false,
false,
false.
则false.
故答案是:false.
【考点】解直角三角形的应用
15.【答案】1
【解析】根据互余两角的三角函数的关系、特殊角的三角函数值就可以求解.
解:false.
【考点】特殊角的三角函数值
16.【答案】false
【解析】利用特殊角的三角函数值以及互余两角的锐角三角函数关系得出false的取值范围.
解:false,
false,
false.
故答案为:false.
【考点】锐角三角函数的增减性
17.【答案】false
【解析】利用勾股定理求出false的长,再由false可得答案.
解:由题意可知,false,false,false,false,
false,
false,
故答案为:false.
【考点】锐角三角函数的定义
18.【答案】false
【解析】根据锐角三角函数的定义可得false,然后根据题目所给false可求解.
解:false,false分别是false对边,false,false,false,false.
故答案为:false.
【考点】锐角三角函数的定义
19.【答案】6
【解析】根据三角函数值直接求出false的长即可.
false,
false,解得false.
【考点】锐角三角函数的定义
20.【答案】100
【解析】由坡度的意义可得出两直角边的关系,进而求出斜边.
根据坡度可得:false,根据false,则false.
【考点】解直角三角形的应用—坡度坡角问题
三、
21.【答案】解:原式false.
【解析】根据二次根式,负指数幂,绝对值,特殊角的三角函数值等性质计算即可得出答案.
【考点】实数的运算,负整数指数幂的运算性质,二次根式的性质与化简,特殊角的三角函数值,实数的绝对值
22.【答案】(1)在false中,false是false边上的高,
false.
在false中,false,false,false,
false.
在false中,false,false,false,
false.
false.
false.
(2)false是false边上的中线,
false,
false,
false.
【解析】解直角三角形
(1)先由三角形的高的定义得出false,再解false,得出false;解false,得出false,根据勾股定理求出false,然后根据false即可求解;
(2)先由三角形的中线的定义求出false的值,则false,然后在false中根据正切函数的定义即可求解.
【考点】解直角三角形
23.【答案】解:作false,垂足为false.
设false,
false,
false,
false,
false,
false,且false,
false,
解得,false,
答:则河的宽度为false
【解析】作false,垂足为false.利用解直角三角形的知识进行求解即可.
【考点】解直角三角形的应用
24.【答案】解:如图,
在false中,false,
false,
false,
false,
false,false,
false,
false,
false,
在false中,false.
故这艘轮船的航行路程false的长度是false.
【解析】首先在false中,根据特殊锐角三角函数值和三角函数的定义可求得false的长,进一步求出false,然后,再证明false,依据相似三角形的性质可求得false的长,最后,在false中根据三角函数可求这艘轮船的航行路程false的长度.
【考点】解直角三角形的应用—仰角俯角问题
25.【答案】解:过点false作false于点false,则四边形false为矩形,false,
在false中,false,false,
false,
false,
在false中,false,
false.
【解析】过点false作false于点false,可得四边形false为矩形,根据false处测得电线杆上false处得仰角为false,在false中求出false的长度,然后在false中求出false的长度.
【考点】矩形的性质,解直角三角形的应用—仰角俯角问题
26.【答案】解:如图,过点false作false于点false.
由题意知false.
在false中,false,false.
false点false在点false的北偏东false方向上,false.
在false中,false.
false,
false
【解析】过点false作false于点false,根据方位角,在false中,求出false;然后在false中,求出false.
【考点】解直角三角形的应用—方向角问题
27.【答案】解:过点false作false于点false,
在false中,false,false,false,
false.
在false中,false,false,false,
false
false.
【解析】根据已知底端B的俯角为false,添加辅助线过点false作false于点false,先在false中,利用锐角三角函数的定义求出false的长,再在false中,利用false的正切求出false的长,然后根据false,求出false的长即可.
【考点】锐角三角函数的定义,特殊角的三角函数值,解直角三角形的应用—仰角俯角问题
28.【答案】解:false在false中,false,false,
false,
在false中,false,
false,
false.
false.
答:路况显示牌false是false
【解析】在false中,知道了已知角的对边,可用正切函数求出邻边false的长;同理在false中,知道了已知角的邻边,用正切值即可求出对边false的长;进而由false得解.
【考点】解直角三角形的应用
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
