七年级数学苏科版下册:7.5.1 三角形及多边形的内角和 同步课件(22张PPT)
文档属性
| 名称 | 七年级数学苏科版下册:7.5.1 三角形及多边形的内角和 同步课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 00:00:00 | ||
图片预览




文档简介
7.5.1 三角形及多边形的内角和
学习目标:
1.掌握三角形的内角和(已经学过);
2.三角形内角和的证明方法;
3.掌握多边形的内角和(重点);
4.多边形的内角和的推导方法;
重难点:
多边形内角和公式、对角线公式;
一.三角形的内角和:
(一)三角形内角和:在小学里,同学们就会用拼图的方法得出:
定理1:三角形内角和等于180°
还有什么方法证明这个规律呢?
一.三角形的内角和:
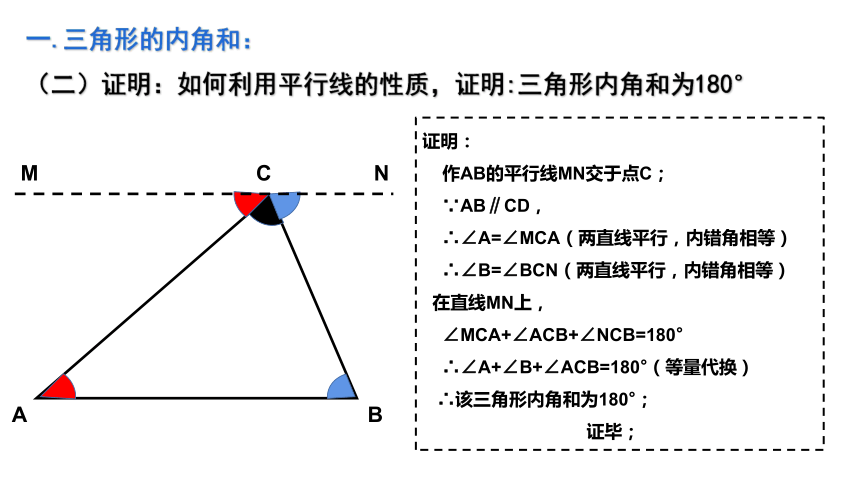
(二)证明:如何利用平行线的性质,证明:三角形内角和为180°
A
B
C
证明:
作AB的平行线MN交于点C;
∵AB∥CD,
∴∠A=∠MCA(两直线平行,内错角相等)
∴∠B=∠BCN(两直线平行,内错角相等)
在直线MN上,
∠MCA+∠ACB+∠NCB=180°
∴∠A+∠B+∠ACB=180°(等量代换)
∴该三角形内角和为180°;
证毕;
M
N
一.三角形的内角和:
(三)辅助线:是利用题目中的已知条件画出的有助于解题的线段/直线;
*.注意:
1.辅助线可以是直线,也可以是线段;
2.作辅助线的时候一定要把步骤说的明明白白,叙述具有唯一性;
3.常见的辅助线作法:
(1)连接AB;
(2)作直线AB⊥CD于D;
(3)作AB的平行线MN交于点C;
【警告】一个题目中,尽量不要使用辅助线,目前的题目也很少用到辅助线,不要做作地给一道不需要的题加上辅助线,画蛇添足!
练习:
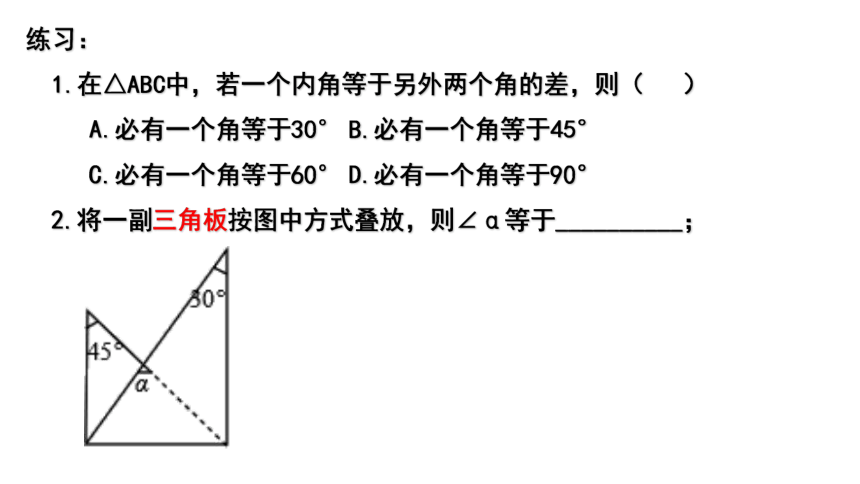
1.在△ABC中,若一个内角等于另外两个角的差,则( )
A.必有一个角等于30° B.必有一个角等于45°
C.必有一个角等于60° D.必有一个角等于90°
2.将一副三角板按图中方式叠放,则∠α等于__________; ? ? ? ??
二.多边形:
(一)多边形的定义:三条或三条以上的线段首尾顺次连接所组成的封闭图形叫做多边形。
这个定义似曾相识?
*.三角形:三条线段首尾顺次连接所组成的封闭图形;
思考:三角形和多边形的区别和相同点?
相同点
首尾相连
封闭图形
区别:多边形可以是不止三条边;
二.多边形:
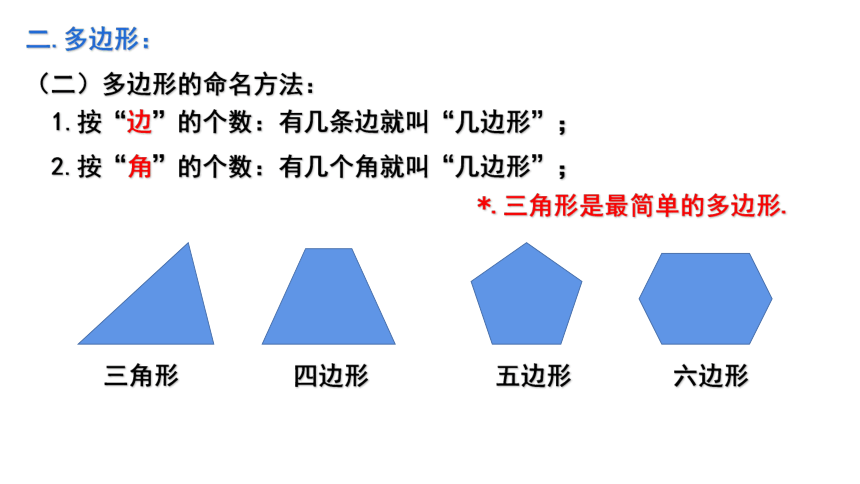
(二)多边形的命名方法:
1.按“边”的个数:有几条边就叫“几边形”;
2.按“角”的个数:有几个角就叫“几边形”;
三角形 四边形 五边形 六边形
*.三角形是最简单的多边形.
二.多边形:
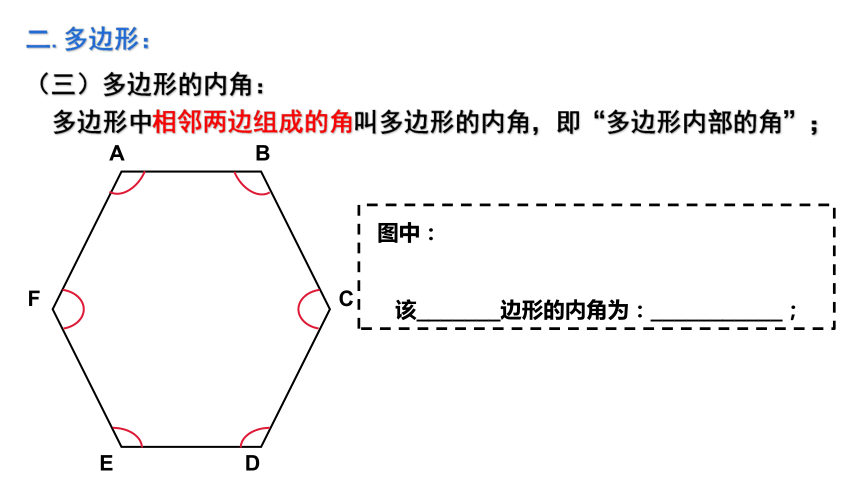
(三)多边形的内角:
多边形中相邻两边组成的角叫多边形的内角,即“多边形内部的角”;
A B
F C
E D
图中:
该_______边形的内角为:___________;
二.多边形:
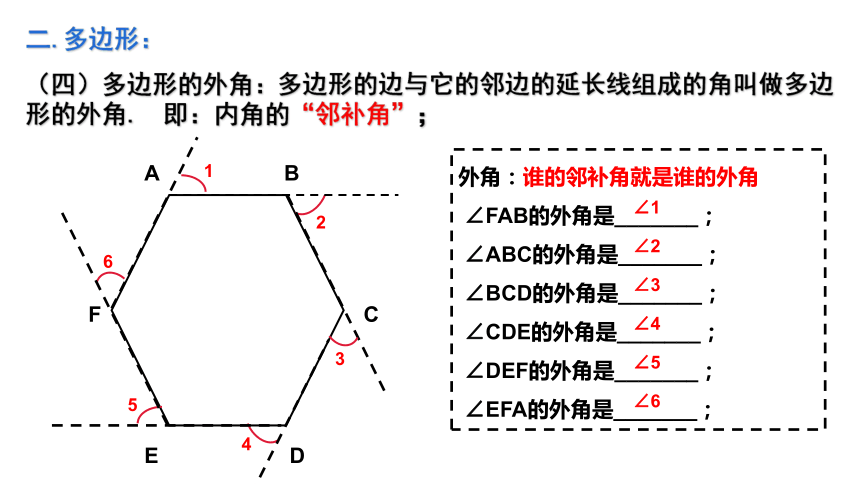
(四)多边形的外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
即:内角的“邻补角”;
A B
F C
E D
外角:谁的邻补角就是谁的外角
∠FAB的外角是_______;
∠ABC的外角是_______;
∠BCD的外角是_______;
∠CDE的外角是_______;
∠DEF的外角是_______;
∠EFA的外角是_______;
1
2
6
5
4
3
∠1
∠2∠3
∠4∠5∠6
二.多边形:
(五)正多边形:
边和内角全部相等的多边形;
(1)正三角形 (2)正四边形
60°
60°
60°
90°
90°
90°
90°
二.多边形:
(六)多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
{8A107856-5554-42FB-B03E-39F5DBC370BA}
图形
三角形
四边形
五边形
六边形
对角线
0
2
5
9
结论:n边形的对角线个数为:n(n-3)÷2
二.多边形:
*.补充:菱形
1.有一组邻边相等的平行四边形。
2.四条边都相等的四边形。
3. 对角线互相垂直的平行四边形。
菱形
1.有一组邻边相等
2.四条边都相等
3. 对角线互相垂直
菱形的判定
菱形的性质
练习:下列说法正确的是( )
A.对角线相等且互相垂直的四边形是菱形
B.对角线互相垂直的平行四边形是正方形
C.对角线相等且互相平分的四边形是矩形
D.对角线互相垂直的菱形是正方形
二.多边形的内角和:
(一)探究四边形的内角和:
A B
C D
(1)四边形ABCD内角为
∠A
∠B
∠C
∠D
(2)连接对角线AD,将四边形分成两个三角形
△ABD
△ACD
∠BAD
∠BDA
∠B
∠CAD
∠ADC
∠C
180°
180°
360°
结论:四边形的内角和为360°
二.多边形的内角和:
(二)探究五边形的内角和:
(1)四边形ABCD内角为
∠A
∠B
∠C
∠D
∠E
(2)连接对角线AD,AC,将五边形分成三个三角形
△ABC
△ACD
△AED
∠CAB∠B
∠ACB
∠CAD
∠ADC
∠DCA
180°
180°
540°
结论:五边形的内角和为540°
A
E B
D C
∠EAD
∠E
∠EDA
180°
二.多边形的内角和:
(三)多边形内角和的规律:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
多边形
三角形
四边形
五边形
六边形
可以分为几个三角形
内角和
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=760°
结论: n变形的内角和为: (n-2)×180°
4
3
2
1
二.多边形的内角和:
(四)注意:
1.当题目中告诉“多边形内角相等时:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}多边形
三角形
四边形
五边形
六边形
内角和
180°
360°
540°
720°
每个内角角度
60°
90°
108°
120°
重点,必须背诵!
练习:
1.一个正多边形的边长为2,每个内角为135°,则这个多边形的周长是_______________;
2.已知从多边形的一个顶点引出的对角线把多边形分为10个三角形,则此多边形内角和是_________;
3.下列结论中错误的是( )
A.三角形的内角和等于180°
B.三角形的外角和小于四边形的外角和
C.五边形的内角和等于540°
D.正六边形的一个内角等于120°?
练习:
4.一个边形,除了一个内角外,其余(n-1)个内角和为2770°,则这个内角是________度.
5.如图,∠A+∠B+∠C+∠D+∠E=__________;
练习:
6.等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠=41°,∠2=51°,那么∠3的度数等于________.
二.多边形的内角和:
(四)注意:
2.切掉多边形的一个角:
4条边
3条边
5条边
4条边
切掉多边形的一个角时,得到的图形的边数可能:
①.不变;②.+1;③.-1;
练习:
1.一个四边形切掉一个角后变成( )
A.四边形
B.五边形
C.四边形或五边形
D.三角形或四边形或五边形?
2.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,求原多边形的边数.
学习目标:
1.掌握三角形的内角和(已经学过);
2.三角形内角和的证明方法;
3.掌握多边形的内角和(重点);
4.多边形的内角和的推导方法;
重难点:
多边形内角和公式、对角线公式;
一.三角形的内角和:
(一)三角形内角和:在小学里,同学们就会用拼图的方法得出:
定理1:三角形内角和等于180°
还有什么方法证明这个规律呢?
一.三角形的内角和:
(二)证明:如何利用平行线的性质,证明:三角形内角和为180°
A
B
C
证明:
作AB的平行线MN交于点C;
∵AB∥CD,
∴∠A=∠MCA(两直线平行,内错角相等)
∴∠B=∠BCN(两直线平行,内错角相等)
在直线MN上,
∠MCA+∠ACB+∠NCB=180°
∴∠A+∠B+∠ACB=180°(等量代换)
∴该三角形内角和为180°;
证毕;
M
N
一.三角形的内角和:
(三)辅助线:是利用题目中的已知条件画出的有助于解题的线段/直线;
*.注意:
1.辅助线可以是直线,也可以是线段;
2.作辅助线的时候一定要把步骤说的明明白白,叙述具有唯一性;
3.常见的辅助线作法:
(1)连接AB;
(2)作直线AB⊥CD于D;
(3)作AB的平行线MN交于点C;
【警告】一个题目中,尽量不要使用辅助线,目前的题目也很少用到辅助线,不要做作地给一道不需要的题加上辅助线,画蛇添足!
练习:
1.在△ABC中,若一个内角等于另外两个角的差,则( )
A.必有一个角等于30° B.必有一个角等于45°
C.必有一个角等于60° D.必有一个角等于90°
2.将一副三角板按图中方式叠放,则∠α等于__________; ? ? ? ??
二.多边形:
(一)多边形的定义:三条或三条以上的线段首尾顺次连接所组成的封闭图形叫做多边形。
这个定义似曾相识?
*.三角形:三条线段首尾顺次连接所组成的封闭图形;
思考:三角形和多边形的区别和相同点?
相同点
首尾相连
封闭图形
区别:多边形可以是不止三条边;
二.多边形:
(二)多边形的命名方法:
1.按“边”的个数:有几条边就叫“几边形”;
2.按“角”的个数:有几个角就叫“几边形”;
三角形 四边形 五边形 六边形
*.三角形是最简单的多边形.
二.多边形:
(三)多边形的内角:
多边形中相邻两边组成的角叫多边形的内角,即“多边形内部的角”;
A B
F C
E D
图中:
该_______边形的内角为:___________;
二.多边形:
(四)多边形的外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
即:内角的“邻补角”;
A B
F C
E D
外角:谁的邻补角就是谁的外角
∠FAB的外角是_______;
∠ABC的外角是_______;
∠BCD的外角是_______;
∠CDE的外角是_______;
∠DEF的外角是_______;
∠EFA的外角是_______;
1
2
6
5
4
3
∠1
∠2∠3
∠4∠5∠6
二.多边形:
(五)正多边形:
边和内角全部相等的多边形;
(1)正三角形 (2)正四边形
60°
60°
60°
90°
90°
90°
90°
二.多边形:
(六)多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
{8A107856-5554-42FB-B03E-39F5DBC370BA}
图形
三角形
四边形
五边形
六边形
对角线
0
2
5
9
结论:n边形的对角线个数为:n(n-3)÷2
二.多边形:
*.补充:菱形
1.有一组邻边相等的平行四边形。
2.四条边都相等的四边形。
3. 对角线互相垂直的平行四边形。
菱形
1.有一组邻边相等
2.四条边都相等
3. 对角线互相垂直
菱形的判定
菱形的性质
练习:下列说法正确的是( )
A.对角线相等且互相垂直的四边形是菱形
B.对角线互相垂直的平行四边形是正方形
C.对角线相等且互相平分的四边形是矩形
D.对角线互相垂直的菱形是正方形
二.多边形的内角和:
(一)探究四边形的内角和:
A B
C D
(1)四边形ABCD内角为
∠A
∠B
∠C
∠D
(2)连接对角线AD,将四边形分成两个三角形
△ABD
△ACD
∠BAD
∠BDA
∠B
∠CAD
∠ADC
∠C
180°
180°
360°
结论:四边形的内角和为360°
二.多边形的内角和:
(二)探究五边形的内角和:
(1)四边形ABCD内角为
∠A
∠B
∠C
∠D
∠E
(2)连接对角线AD,AC,将五边形分成三个三角形
△ABC
△ACD
△AED
∠CAB∠B
∠ACB
∠CAD
∠ADC
∠DCA
180°
180°
540°
结论:五边形的内角和为540°
A
E B
D C
∠EAD
∠E
∠EDA
180°
二.多边形的内角和:
(三)多边形内角和的规律:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
多边形
三角形
四边形
五边形
六边形
可以分为几个三角形
内角和
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=760°
结论: n变形的内角和为: (n-2)×180°
4
3
2
1
二.多边形的内角和:
(四)注意:
1.当题目中告诉“多边形内角相等时:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}多边形
三角形
四边形
五边形
六边形
内角和
180°
360°
540°
720°
每个内角角度
60°
90°
108°
120°
重点,必须背诵!
练习:
1.一个正多边形的边长为2,每个内角为135°,则这个多边形的周长是_______________;
2.已知从多边形的一个顶点引出的对角线把多边形分为10个三角形,则此多边形内角和是_________;
3.下列结论中错误的是( )
A.三角形的内角和等于180°
B.三角形的外角和小于四边形的外角和
C.五边形的内角和等于540°
D.正六边形的一个内角等于120°?
练习:
4.一个边形,除了一个内角外,其余(n-1)个内角和为2770°,则这个内角是________度.
5.如图,∠A+∠B+∠C+∠D+∠E=__________;
练习:
6.等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠=41°,∠2=51°,那么∠3的度数等于________.
二.多边形的内角和:
(四)注意:
2.切掉多边形的一个角:
4条边
3条边
5条边
4条边
切掉多边形的一个角时,得到的图形的边数可能:
①.不变;②.+1;③.-1;
练习:
1.一个四边形切掉一个角后变成( )
A.四边形
B.五边形
C.四边形或五边形
D.三角形或四边形或五边形?
2.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,求原多边形的边数.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
