第一章第2节感应电动势与电磁感应定律

(共33张PPT)
问题1：据前面所学，电路中存在持续电流的条件是什么？
问题2：什么叫电磁感应现象？产生感应电流的条件是什么？
（1）闭合电路；
（2）有电源
产生感应电流的条件是：
（1）闭合电路；（2）磁通量变化。
利用磁场产生电流的现象
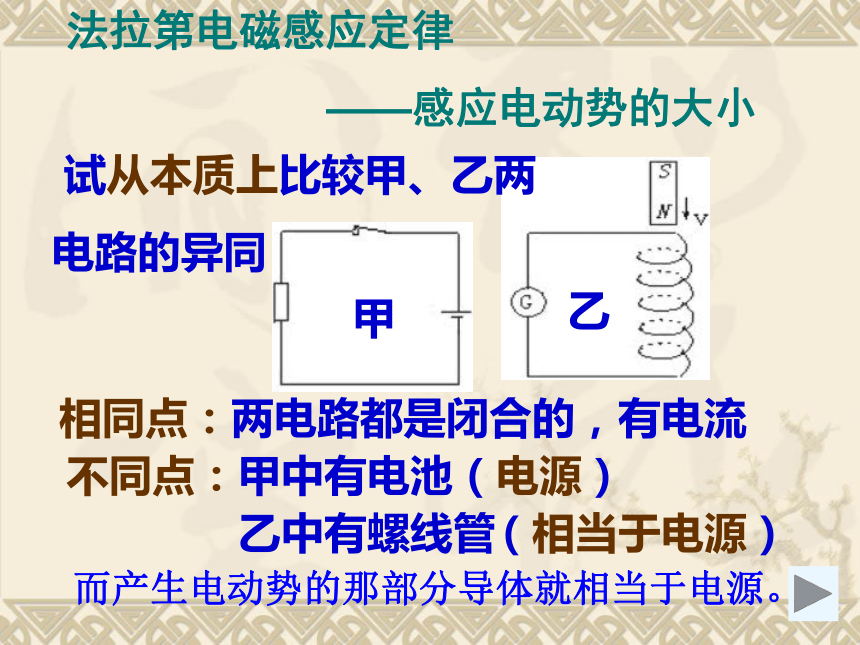
法拉第电磁感应定律
——感应电动势的大小
试从本质上比较甲、乙两
电路的异同
乙
甲
相同点：两电路都是闭合的，有电流
不同点：甲中有电池（电源）
乙中有螺线管
（相当于电源）
而产生电动势的那部分导体就相当于电源。
一、感应电动势
（E）
法拉第电磁感应定律
——感应电动势的大小
1.定义:
在电磁感应现象中产生的电动势。
既然闭合电路中有感应电流，这个电路中就一定有感应电动势。
⑶产生感应电流只不过是一个现象，它表示电路中在输送着电能；而产生感应电动势才是电磁感应现象的本质，它表示电路已经具备了随时输出电能的能力。
几点说明：
⑴不论电路是否闭合，只要穿过电路的磁通量发生变化，电路中就产生感应电动势，产生感应电动势是电磁感应现象的本质。
⑵磁通量是否变化是电磁感应的根本原因。若磁通量变化了，电路中就会产生感应电动势，再若电路又是闭合的，电路中将会有感应电流。
Φ变化
产生E
产生I
总电阻一定时，E越大，I越大，指针偏转越大。
Φ变化的快慢不同
Φ都发生了变化
问题1：在实验中，电流表指针偏转原因是什么？
问题2：电流表指针偏转程度跟感应电动势的大小有什么关系？
观察实验，分析并思考回答下面的问题：
问题3：该实验中，将条形磁铁从同一高度插入线圈中，快插入和慢插入有什么相同和不同？
从条件上看
从结果上看
相同
不同
都产生了I
产生的I大小不等
一、感应电动势
（E）
§16.2 法拉第电磁感应定律
——感应电动势的大小
1.定义:
在电磁感应现象中产生的电动势。
2．磁通量变化越快，感应电动势越大。
磁通量变化
磁通量变化快慢
磁通量
磁通量Φ与时刻t对应，磁通量的变化量是两个时刻穿过这个面的磁通量之差，即ΔΦ＝Φ2-Φ1，磁通量的变化率是单位时间内磁通量的变化量，计算公式是ΔΦ／Δt，磁通量变化率的大小不是单纯由磁通量的变化量决定，还跟发生这个变化所用的时间有关。
穿过一个面的磁通量大，但磁通量的变化量不一定大，磁通量的变化率也不一定大；同理，穿过一个面的磁通量的变化量大，但磁通量不一定大，磁通量的变化率也不一定大；穿过一个面的磁通量的变化率大，但磁通量和磁通量的变化量都不一定大。
应用举例
例1、如图所示为穿过某线路的磁通量Φ随
时间t变化的关系图，试根据图说明：
（1）穿过某线路的磁通量Φ何时最大？
何时最小？
（2）Δφ/Δt何时最大？何时最小？
（3）感应电动势E何时最大？何时最小？
Φ
t
O
t1
t2
t3
t4
注意区分几个物理量：
①Φ、Δφ、Δφ/Δt
②E只与Δφ/Δt有关，
而与Φ、Δφ无关。
一、感应电动势
（E）
§16.2 法拉第电磁感应定律
——感应电动势的大小
1.定义:
在电磁感应现象中产生的电动势。
2．磁通量变化越快，感应电动势越大。
电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比。
二、法拉第电磁感应定律
1.内容:
(K是一个常数)
(n为线圈的匝数)
一、感应电动势
（E）
§16.2 法拉第电磁感应定律
——感应电动势的大小
电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比。
二、法拉第电磁感应定律
1.内容:
(n为线圈的匝数)
2.数学表达式:
平均磁通变化率
平均感应电动势
巩固练习：
√
1．穿过一个单匝线圈的磁通量始终为每秒钟均匀地增加2 Wb，则：
A．线圈中的感应电动势每秒钟增加2 V
B．线圈中的感应电动势每秒钟减少2 V
C．线圈中的感应电动势始终是2 V
D．线圈中不产生感应电动势
2．一个矩形线圈，在匀强磁场中绕一个固定轴做匀速转动，当线圈处于如图所示位置时，它的： A.磁通量最大,磁通量变化率最大,感应电动势最大
B.磁通量最小,磁通量变化率最大,感应电动势最大
C.磁通量最大,磁通量变化率最小,感应电动势最大
D.磁通量最小,磁通量变化率最小,感应电动势最大
3．如右图所示的匀强磁场中，B=0.4 T，导体ab长L=40 cm，电阻R ab=0.5 Ω，框架电阻不计，当导体ab以v=5 m/s的速度匀速向左运动时，电路中产生的感应电流为 。
1.6A
√
三、重要的推论
如图所示闭合线圈一部分导体ab处于匀强磁场中，磁感应强度是B，ab以速度v匀速切割磁感线，求产生的感应电动势。
回路在时间t内增大的面积为：
ΔS=LvΔt
解：
产生的感应电动势为：
穿过回路的磁通量的变化为：
ΔΦ=BΔS
v
θ
B
V2
V1
=Vsinθ
=Vcosθ
若导体斜切磁感线
（θ为v与B夹角）
=BLvΔt
感应电动势
L
v
B
公式BLv中的L指的是切割磁感线的有效长度。在上图中E=BLv，L是圆弧切割磁感线的有效长度。
思考题
求下面图示情况下，a、b、c三段导体两端的感应电动势各为多大？
一、感应电动势
（E）
§16.2 法拉第电磁感应定律
——感应电动势的大小
1.定义:
在电磁感应现象中产生的电动势。
2．磁通量变化越快，感应电动势越大。
电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比。
二、法拉第电磁感应定律
1.内容:
(n为线圈的匝数)
2.数学表达式:
三、重要的推论
（θ为v与B夹角）
四.反电动势
1.既然线圈在磁场中转动,线圈中就会产生感应电动势.感应电动势加强了电源了产生的电流,还是削弱了它 是有得于线圈的转动,还是阻碍了线圈的转动
电动机转动是时,线圈中产生的感应电动势
总要削弱电源电动势的作用,阻碍线圈的转动.
-----反电动势
2.电动机由于机械故障停转,要立即切断电源.
用公式E＝nΔΦ／Δt求E的三种情况：
1.磁感应强度B不变，垂直于磁场的回路面积S发生变化，ΔS＝S2-S1，此时，E＝nBΔS／Δt。
2.垂直于磁场的回路面积S不变，磁感应强度B发生变化，ΔB＝B2-B1，此时，E＝nSΔB／Δt。
3.磁感应强度B和垂直于磁场的回路面积S都发生变化，此时E＝nΔBΔS／Δt。
例：如图所示，一个50匝的线圈的两端跟R＝99Ω的电阻相连接，置于竖直向下的匀强磁场中，线圈的横截面积是20㎝2，电阻为1Ω，磁感应强度以100T／s的变化率均匀减少。在这一过程中通过电阻R的电流为多大？
解析：
两块水平放置的板间距为d，用导线与一n匝线圈连接，线圈置于方向竖直向上的匀强磁场中，如图所示，两板间有一质量为m、带电量为＋q的油滴恰好静止，则线圈中的磁通量的变化率是多少？
（mgd/nq）
公式E＝nΔΦ/Δt与E=BLvsinθ的区别和联系：
1.区别：一般来说E＝nΔΦ/Δt，求出的是Δt时间内的平均感应电动势，E与某段时间或某个过程相对应，常在穿过一个面的磁通量发生变化时用。E=BLvsinθ求出的是瞬时感应电动势，E与某个时刻或某个位置相对应，常在一部分导体做切割磁感线运动时用。
2.联系：公式E＝nΔΦ/Δt和公式E=BLvsinθ是统一的。公式E＝nΔΦ/Δt中当Δt→0时，求出的E为瞬时感应电动势；公式E=BLvsinθ中当V代入平均速度时，则求出的E为平均感应电动势。
例：半径为r、电阻为R的金属环通过某直径的轴OO’以角速度ω做匀速转动，如图所示。匀强磁场的磁感应强度为B，从金属环的平面的磁场方向重合时开始计时，则在转过30 的过程中。求：
(1)环中产生的感应电动势的平均值是多大？
(2)金属环某一横截面内通过的电荷量是多少？
解析：
求感应电动势的平均值时，一般要用公式E＝nΔΦ/Δt。
(1)金属环在转过30 的过程中，磁通量的变化量
(2)金属环某一横截面内通过的电荷量是多少？
由于E＝ΔΦ/Δt，I＝E／R，I＝Q／Δt，所以
如图所示，一个500匝的线圈的两端跟R＝99Ω的电阻相连接，置于竖直向下的匀强磁场中，线圈的横截面积是20㎝2，电阻为1Ω，磁场的磁感应强度随时间变化的图象如图所示。求磁场变化过程中通过电阻R的电流为多大？
解析：
由图b知，线圈中磁感应强度B均匀增加，其变
化率ΔB／Δt=(50-10)/4=10T/s.
例：如图所示，裸金属线组成滑框，ab可滑
动，其电阻为r，长为L，串接电阻R，匀强磁场为B，当ab以V向右匀速运动过程中，求：
（1）ab间感应电动势。
（2）ab间的电压。
（3）保证ab匀速运动，所加外力F。
（4）在2秒的时间内，外力功；ab生热Q；电阻 R上生热。
如图所示，导线全部为裸导线，半径为r的圆导线处在垂直于圆平面的匀强磁场中，磁感应强度为B，方向如图。一根长度大于2r的直导线MN，以速率V在圆上自左端匀速滑到右端，电路中定值电阻为R，其余电阻忽略不计。在滑动过程中，通过电阻R的电流的平均值为__________;当MN从圆环左端滑到右端的过程中，通过R的电荷量为_________,当MN通过圆环中心O时，通过R的电流为_________.
(πBrv/2R, πBr2/R,2Brv/R)
如图所示，长为L的金属杆OA绕过O点垂直于纸面的固定轴沿顺时针方向匀速转动，角速度为ω。一匀强磁场垂直于纸面向里，磁感应强度为B，磁场范围足够大。求OA杆产生感应电动势的大小。
解析：
由于OA杆是匀速转动，故OA产生的感应电动势是恒定的，其平均值与瞬时值相同，求感应电动势的两个公式均可以用。
解法一：用E＝BLV求E，V应为平均切割速率，棒上各小段的速率是不相同的，因O点速率V0＝0，由V＝rω知棒上各点线速度跟旋转半径成正比，
所以棒切割磁感线的平均速率为
V＝（V0＋VA）／2＝ωL／2
则E＝BLV＝BωL2／2
解法二：用E＝nΔΦ/Δt求E。设经过Δt时间，OA棒扫过的扇形面积为ΔS，如图所示，ΔS＝LωΔtL／2＝L2ωΔt／2，变化的磁通量为E＝ΔΦ/Δt＝BΔS／Δt＝BL2ω／2.
直导线绕其一端转动时产生的感应电动势 ：
E＝BL2ω／2
ω
A
B
C
R
O
例：如图所示，在磁感应强度为B的匀强磁场中，有半径为r的光滑半圆形导体框架。OC
为一端绕O点在框架上滑动的导体棒，OA之
间连一个阻值为R的电阻（其余电阻都不计），
若使OC以角速度ω匀速转动。试求：
（1）图中哪部分相当于电源？
（2）感应电动势E为多少？
（3）流过电阻R的电流I为多少？
如图2所示，导线OMN在与磁场方向垂直的平面内，以角速度ω在匀强磁场中沿逆时针方向绕O点匀速转动，磁感应强度为B，方向垂直指向纸里，MN的电动势多大？
解析：由于MN上各点的切割速度不等，应当用MN上各点的平均速度也就是MN中点的速度进行计算．
设OM=r1，ON=r2，则