立体几何初步水平测试(3)
图片预览


文档简介
立体几何初步水平测试(3)
1.已知正方体外接球的体积是,那么正方体的棱长等于 ( )
(A) (B) (C) (D)
2.表面积为 的正八面体的各个顶点都在同一个球面上,则此球的体积为
A. B. C. D.
3.给出以下四个命题
①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;
③如果两条直线都平行于一个平面,那么这两条直线互相平行;
④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直.
其中真命题的个数是
A.4 B.3 C.2 D.1
4.已知平面外不共线的三点到的距离都相等,则正确的结论是 ( )
(A)平面ABC必不垂直于
(B)平面ABC必平行于
(C)平面ABC必与相交
(D)存在的一条中位线平行于或在内
5.正四棱锥底面边长为4,侧棱长为3,则其体积为 .
6.如图,平面α⊥平面β,A∈α,B∈β,
AB与两平面α、β所成的角分别为和,过A、B分别作两平
面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )
(A)2∶1 (B)3∶1
(C)3∶2 (D)4∶3
7.已知球的半径是,三点都在球面上,两点和两点的球面距离都是,两点的球面距离是,则二面角的大小是( )
(A) (B) (C) (D)
8.设、是两条不同的直线,、是两个不同的平面.考查下列命题,其中正确的命题是( )
A. B.
C. D.
9. 关于直线、与平面、,有下列四个命题:
①且,则; ②且,则;
③且,则; ④且,则.
其中真命题的序号是:(D)
A. ①、② B. ③、④ C. ①、④ D. ②、③
10.已知正四棱锥的体积为12,底面对角线的长为,则侧面与底面所成的二面角等于_______________。
11.如图,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A-BEFD与三棱锥A-EFC的表面积分别是S1,S2,则必有( )
S1S2
S1S2
S1=S2
S1,S2的大小关系不能确定
12.给出下列四个命题:
①垂直于同一直线的两条直线互相平行.
②垂直于同一平面的两个平面互相平行.
③若直线与同一平面所成的角相等,则互相平行.
④若直线是异面直线,则与都相交的两条直线是异面直线.
其中假命题的个数是
(A)1 (B)2 (C)3 (D)4
13.已知三点在球心为,半径为的球面上,,且,那么两点的球面距离为_______________,球心到平面的距离为______.
14.正四面体ABCD的棱长为1,棱AB∥平面α,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是 .
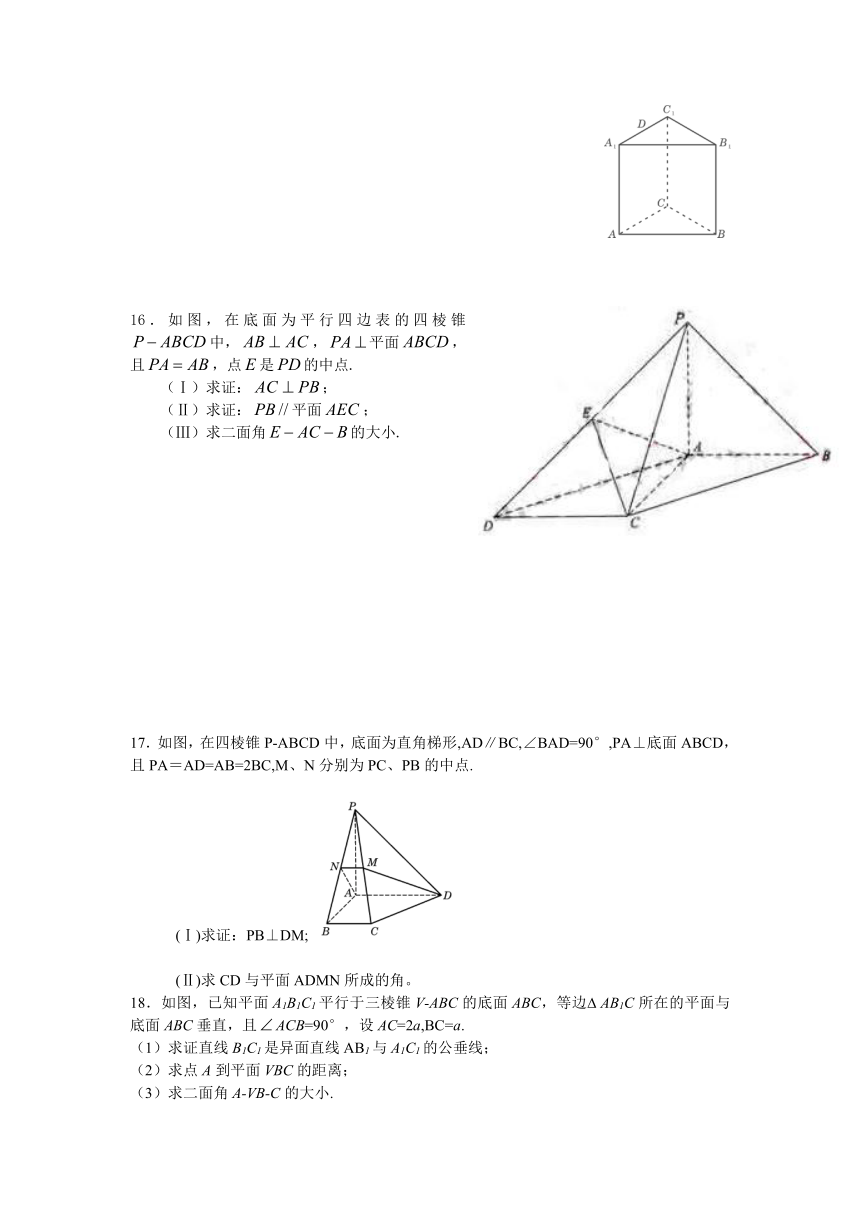
15.如图,已知正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的 中点,则直线AD 与平面B1DC所成角的正弦值为 .
16.如图,在底面为平行四边表的四棱锥中,,平面,且,点是的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面;
(Ⅲ)求二面角的大小.
17.如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求CD与平面ADMN所成的角。
18.如图,已知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边 AB1C所在的平面与底面ABC垂直,且ACB=90°,设AC=2a,BC=a.
(1)求证直线B1C1是异面直线AB1与A1C1的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角A-VB-C的大小.
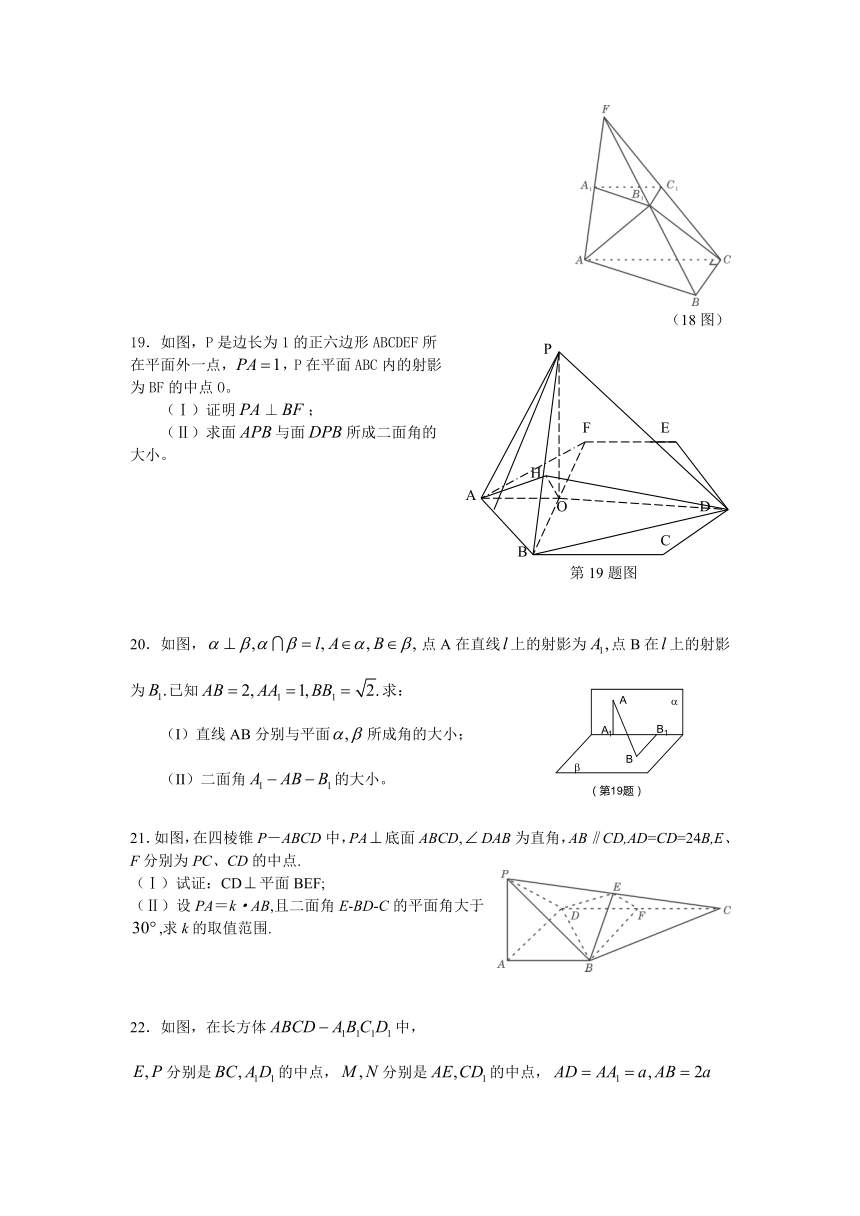
(18图)
19.如图,P是边长为1的正六边形ABCDEF所在平面外一点,,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明⊥;
(Ⅱ)求面与面所成二面角的大小。
20.如图,点A在直线上的射影为点B在上的射影为已知求:
(I)直线AB分别与平面所成角的大小;
(II)二面角的大小。
21.如图,在四棱锥P-ABCD中,PA底面ABCD,DAB为直角,AB‖CD,AD=CD=24B,E、F分别为PC、CD的中点.
(Ⅰ)试证:CD平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于,求k的取值范围.
22.如图,在长方体中,
分别是的中点,分别是的中点,
(Ⅰ)求证:面;
(Ⅱ)求二面角的大小。
(Ⅲ)求三棱锥的体积。
23.如图,在五面体中,点是矩形的对角线的交点,面是等边三角形,棱.
(1)证明//平面;
(2)设,证明平面.
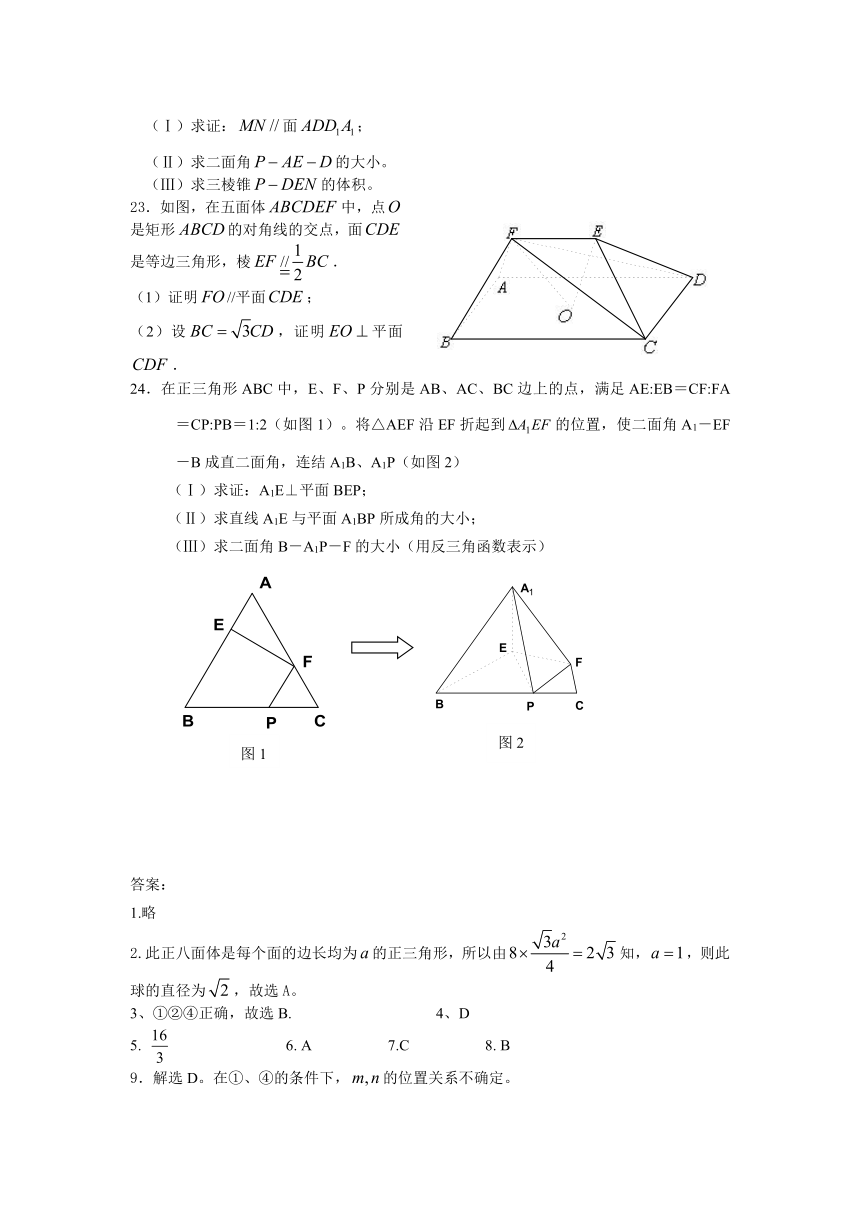
24.在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示)
答案:
1.略
2.此正八面体是每个面的边长均为的正三角形,所以由知,,则此球的直径为,故选A。
3、①②④正确,故选B. 4、D
5. 6. A 7.C 8. B
9.解选D。在①、④的条件下,的位置关系不确定。
10.底面正方形面积,底面边长,高,
二面角的余切值。
代入数据,得:
。
又必为锐角,所以。
11. 解:连OA、OB、OC、OD
则VA-BEFD=VO-ABD+VO-ABE+VO-BEFD
VA-EFC=VO-ADC+VO-AEC+VO-EFC又VA-BEFD=VA-EFC而每个三棱锥的高都是原四面体的内切球的半径,故SABD+SABE+SBEFD=SADC+SAEC+SEFC又面AEF公共,故选C
12. 【解析】利用特殊图形正方体我们不难发现①、②、③、④均不正确,故选择答案D。
【点评】本题考查了空间线面的位置关系以及空间想象能力,同时考查了立体几何问题处理中运用特殊图形举例反证的能力。
13. 14. 15. 4/5
16. (Ⅰ)略;(Ⅱ)略;(Ⅲ)。 17.略 18.(1);(2)。
19. 解:(Ⅰ)在正六边形ABCDEF中,为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;∵O为BF中点,∴AO⊥BF,∴PA⊥BF。 (Ⅱ)略
20.解法一: (Ⅰ)如图, 连接A1B,AB1, ∵α⊥β, α∩β=l ,AA1⊥l, BB1⊥l,
∴AA1⊥β, BB1⊥α. 则∠BAB1,∠ABA1分别是AB与α和β所成的角.
Rt△BB1A中, BB1= , AB=2, ∴sin∠BAB1 = = . ∴∠BAB1=45°.
Rt△AA1B中, AA1=1,AB=2, sin∠ABA1= = , ∴∠ABA1= 30°.
故AB与平面α,β所成的角分别是45°,30°.
(Ⅱ) ∵BB1⊥α, ∴平面ABB1⊥α.在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB, ∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=. ∴Rt△AA1B中,A1B== = . 由AA1·A1B=A1F·AB得 A1F== = ,
∴在Rt△A1EF中,sin∠A1FE = = , ∴二面角A1-AB-B1的大小为arcsin.
解法二: (Ⅰ)同解法一.
(Ⅱ) 如图,建立坐标系, 则A1(0,0,0),A(0,0,1),B1(0,1,0),B(,1,0).在AB上取一点F(x,y,z),则存在t∈R,使得=t , 即(x,y,z-1)=t(,1,-1), ∴点F的坐标为(t, t,1-t).要使⊥,须·=0, 即(t, t,1-t) ·(,1,-1)=0, 2t+t-(1-t)=0,解得t= , ∴点F的坐标为(,-, ), ∴=(,, ). 设E为AB1的中点,则点E的坐标为(0,, ). ∴=(,-,).
又·=(,-,)·(,1,-1)= - - =0, ∴⊥, ∴∠A1FE为所求二面角的平面角.
又cos∠A1FE= = = = = ,
∴二面角A1-AB-B1的大小为arccos.
21. 解法一:(Ⅰ)证:由已知DF∥AB且DAD为直角,故ABFD是矩形,从而CDBF.
又PA底面ABCD,CDAD,故由三垂线定理知CDPD.在△PDC中,E、F分别
PC、CD的中点,故EF∥PD,从而CDEF,由此得CD面BEF.
(Ⅱ)连结AC交BF于G.易知G为AC的中点.连接EG,则在△PAC中易知EC∥PA.又因
PA底面ABCD,故BC底面ABCD.在底面ABCD中,过C作GHBD,垂足为H,连接EH.由三垂线定理知EHBD.从而EHG为二面角E-BD-C的平面角.
设AB=a,则在△PAC中,有
BG=PA=ka.
以下计算GH,考察底面的平面图(如答(19)图2).连结GD.
因S△CBD=BD·GH=GB·OF.
故GH=.
在△ABD中,因为AB=a,AD=2A,得BD=a 第(41)图2
而GB=FB=AD-a.DF-AB,从而得
GH== =
因此tanEHG==
由k>0知是锐角,故要使>,必须
>tan=
解之得,k的取值范围为k>
解法二:
(Ⅰ)如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为:轴建立空间直角坐标系,设AB=a,则易知点A,B,C,D,F的坐标分别为
A(0,0,0),B(a,0,0),C(2a,2a,0),D(0,2a,0),
F(a,2a,0).
从而=(2a,0,0), =(0,2a,0),
·=0,故 .
设PA=b,则P(0,0,b),而E为PC中点.故
E.从而=.
·=0,故.
由此得CD面BEF.
(Ⅱ)设E在xOy平面上的投影为G,过G作GHBD垂足为H,由三垂线定理知EHBD.
从而EHG为二面角E-BD-C的平面角.
由PA=k·AB得P(0,0,ka),E,G(a,a,0).
设H(x,y,0),则=(x-a,y-a,0), =(-a,2a,0),
由·=0得=a(x-a)+2a(y-a)=0,即
x-2y=-a ①
又因=(x,a,y,0),且与的方向相同,故=,即
2x+y=2a ②
由①②解得x=a,y=a,从而=,||=a.
tanEHG===.
由k>0知, EHC是锐角,由EHC>得tanEHG>tan即
>
故k的取值范围为k>.
22. 本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力和推理能力。满分12分
解法一:(Ⅰ)证明:取的中点,连结
∵分别为的中点
∵
∴面,面
∴面面 ∴面
(Ⅱ)设为的中点
∵为的中点 ∴ ∴面
作,交于,连结,则由三垂线定理得
从而为二面角的平面角。
在中,,从而
在中,
故:二面角的大小为
(Ⅲ)
作,交于,由面得
∴面
∴在中,
∴
方法二:以为原点,所在直线分别为轴,轴,轴,建立直角坐标系,则
∵分别是的中点
∴
(Ⅰ)
取,显然面
,∴
又面 ∴面
(Ⅱ)过作,交于,取的中点,则∵
设,则
又
由,及在直线上,可得:
解得
∴ ∴ 即
∴与所夹的角等于二面角的大小
故:二面角的大小为
(Ⅲ)设为平面的法向量,则
又
∴ 即 ∴可取
∴点到平面的距离为
∵,
∴
∴
23.略
24. 解:不妨设正三角形的边长为3,则
(I)在图1中,取BE的中点D,连结DF,
∵AE∶EB=CF∶FA=1∶2,∴AF=AD=2,而∠A=60o,∴△ADF为正三角形。
又AE=DE=1,∴EF⊥AD。
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的一个平面角,
由题设条件知此二面角为直二面角,∴A1E⊥BE。
又BEEF=E,∴A1E⊥面BEF,即A1E⊥面BEP。
(II)在图2中,∵A1E不垂直于A1B,∴A1E是面A1BP的斜线,又A1E⊥面BEP,∴A1E⊥BP,∴BP垂直于A1E在面A1BP内的射影(三垂线定理的逆定理)
设A1E在面A1BP内的射影为A1Q,且A1Q交BP于Q,
则∠EA1Q就是A1E与面A1BP所成的角,且BP⊥A1Q。
在△EBP中,∵BE=BP=2,∠EBP=60o,∴△EBP为正三角形,∴BE=EP。
又A1E⊥面BEP,∴A1B=A1P,∴Q为BP的中点,且EQ=,而A1E=1,
∴在Rt△A1EQ中,,即直线A1E与面A1BP所成角为60o。
(III)在图3中,过F作FM于M,连结QM、QF。
∵CF=CP=1,∠C=60o,∴△FCP为正三角形,故PF=1,
又PQ=BP=1,∴PF=PQ……①
∵A1E⊥面BEP,EQ=EF=,∴A1F=A1Q,
∴△A1FP△A1QP,故∠A1PF=∠A1PQ……②
由①②及MP为公共边知△FMP△QMP,故∠QMP=∠FMP=90o,且MF=MQ,
∴∠FMQ为二面角B-A1P-F的一个平面角。
在Rt△A1QP中,A1Q=A1F=2,PQ=1,∴A1P=,
∵MQ⊥A1P,∴MQ=,∴MF=。
在△FCQ中,FC=1,QC=2,∠C=60o,由余弦定理得QF=,
在△FMQ中,,
w.w.w.k.s.5.u.c.o.m
www.
α
β
A
B
A′
B′
A
B
C
D
E
F
O
P
第19题图
H
图1
图2
A
B
A1
B1
α
β
l
第20题解法一图
E
F
A
B
A1
B1
α
β
l
第20题解法二图
y
x
y
E
F
图3
Q
M
1.已知正方体外接球的体积是,那么正方体的棱长等于 ( )
(A) (B) (C) (D)
2.表面积为 的正八面体的各个顶点都在同一个球面上,则此球的体积为
A. B. C. D.
3.给出以下四个命题
①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;
③如果两条直线都平行于一个平面,那么这两条直线互相平行;
④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直.
其中真命题的个数是
A.4 B.3 C.2 D.1
4.已知平面外不共线的三点到的距离都相等,则正确的结论是 ( )
(A)平面ABC必不垂直于
(B)平面ABC必平行于
(C)平面ABC必与相交
(D)存在的一条中位线平行于或在内
5.正四棱锥底面边长为4,侧棱长为3,则其体积为 .
6.如图,平面α⊥平面β,A∈α,B∈β,
AB与两平面α、β所成的角分别为和,过A、B分别作两平
面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )
(A)2∶1 (B)3∶1
(C)3∶2 (D)4∶3
7.已知球的半径是,三点都在球面上,两点和两点的球面距离都是,两点的球面距离是,则二面角的大小是( )
(A) (B) (C) (D)
8.设、是两条不同的直线,、是两个不同的平面.考查下列命题,其中正确的命题是( )
A. B.
C. D.
9. 关于直线、与平面、,有下列四个命题:
①且,则; ②且,则;
③且,则; ④且,则.
其中真命题的序号是:(D)
A. ①、② B. ③、④ C. ①、④ D. ②、③
10.已知正四棱锥的体积为12,底面对角线的长为,则侧面与底面所成的二面角等于_______________。
11.如图,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A-BEFD与三棱锥A-EFC的表面积分别是S1,S2,则必有( )
S1S2
S1S2
S1=S2
S1,S2的大小关系不能确定
12.给出下列四个命题:
①垂直于同一直线的两条直线互相平行.
②垂直于同一平面的两个平面互相平行.
③若直线与同一平面所成的角相等,则互相平行.
④若直线是异面直线,则与都相交的两条直线是异面直线.
其中假命题的个数是
(A)1 (B)2 (C)3 (D)4
13.已知三点在球心为,半径为的球面上,,且,那么两点的球面距离为_______________,球心到平面的距离为______.
14.正四面体ABCD的棱长为1,棱AB∥平面α,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是 .
15.如图,已知正三棱柱ABC-A1B1C1的所有棱长都相等,D是A1C1的 中点,则直线AD 与平面B1DC所成角的正弦值为 .
16.如图,在底面为平行四边表的四棱锥中,,平面,且,点是的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面;
(Ⅲ)求二面角的大小.
17.如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求CD与平面ADMN所成的角。
18.如图,已知平面A1B1C1平行于三棱锥V-ABC的底面ABC,等边 AB1C所在的平面与底面ABC垂直,且ACB=90°,设AC=2a,BC=a.
(1)求证直线B1C1是异面直线AB1与A1C1的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角A-VB-C的大小.
(18图)
19.如图,P是边长为1的正六边形ABCDEF所在平面外一点,,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明⊥;
(Ⅱ)求面与面所成二面角的大小。
20.如图,点A在直线上的射影为点B在上的射影为已知求:
(I)直线AB分别与平面所成角的大小;
(II)二面角的大小。
21.如图,在四棱锥P-ABCD中,PA底面ABCD,DAB为直角,AB‖CD,AD=CD=24B,E、F分别为PC、CD的中点.
(Ⅰ)试证:CD平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于,求k的取值范围.
22.如图,在长方体中,
分别是的中点,分别是的中点,
(Ⅰ)求证:面;
(Ⅱ)求二面角的大小。
(Ⅲ)求三棱锥的体积。
23.如图,在五面体中,点是矩形的对角线的交点,面是等边三角形,棱.
(1)证明//平面;
(2)设,证明平面.
24.在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示)
答案:
1.略
2.此正八面体是每个面的边长均为的正三角形,所以由知,,则此球的直径为,故选A。
3、①②④正确,故选B. 4、D
5. 6. A 7.C 8. B
9.解选D。在①、④的条件下,的位置关系不确定。
10.底面正方形面积,底面边长,高,
二面角的余切值。
代入数据,得:
。
又必为锐角,所以。
11. 解:连OA、OB、OC、OD
则VA-BEFD=VO-ABD+VO-ABE+VO-BEFD
VA-EFC=VO-ADC+VO-AEC+VO-EFC又VA-BEFD=VA-EFC而每个三棱锥的高都是原四面体的内切球的半径,故SABD+SABE+SBEFD=SADC+SAEC+SEFC又面AEF公共,故选C
12. 【解析】利用特殊图形正方体我们不难发现①、②、③、④均不正确,故选择答案D。
【点评】本题考查了空间线面的位置关系以及空间想象能力,同时考查了立体几何问题处理中运用特殊图形举例反证的能力。
13. 14. 15. 4/5
16. (Ⅰ)略;(Ⅱ)略;(Ⅲ)。 17.略 18.(1);(2)。
19. 解:(Ⅰ)在正六边形ABCDEF中,为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;∵O为BF中点,∴AO⊥BF,∴PA⊥BF。 (Ⅱ)略
20.解法一: (Ⅰ)如图, 连接A1B,AB1, ∵α⊥β, α∩β=l ,AA1⊥l, BB1⊥l,
∴AA1⊥β, BB1⊥α. 则∠BAB1,∠ABA1分别是AB与α和β所成的角.
Rt△BB1A中, BB1= , AB=2, ∴sin∠BAB1 = = . ∴∠BAB1=45°.
Rt△AA1B中, AA1=1,AB=2, sin∠ABA1= = , ∴∠ABA1= 30°.
故AB与平面α,β所成的角分别是45°,30°.
(Ⅱ) ∵BB1⊥α, ∴平面ABB1⊥α.在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB, ∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=. ∴Rt△AA1B中,A1B== = . 由AA1·A1B=A1F·AB得 A1F== = ,
∴在Rt△A1EF中,sin∠A1FE = = , ∴二面角A1-AB-B1的大小为arcsin.
解法二: (Ⅰ)同解法一.
(Ⅱ) 如图,建立坐标系, 则A1(0,0,0),A(0,0,1),B1(0,1,0),B(,1,0).在AB上取一点F(x,y,z),则存在t∈R,使得=t , 即(x,y,z-1)=t(,1,-1), ∴点F的坐标为(t, t,1-t).要使⊥,须·=0, 即(t, t,1-t) ·(,1,-1)=0, 2t+t-(1-t)=0,解得t= , ∴点F的坐标为(,-, ), ∴=(,, ). 设E为AB1的中点,则点E的坐标为(0,, ). ∴=(,-,).
又·=(,-,)·(,1,-1)= - - =0, ∴⊥, ∴∠A1FE为所求二面角的平面角.
又cos∠A1FE= = = = = ,
∴二面角A1-AB-B1的大小为arccos.
21. 解法一:(Ⅰ)证:由已知DF∥AB且DAD为直角,故ABFD是矩形,从而CDBF.
又PA底面ABCD,CDAD,故由三垂线定理知CDPD.在△PDC中,E、F分别
PC、CD的中点,故EF∥PD,从而CDEF,由此得CD面BEF.
(Ⅱ)连结AC交BF于G.易知G为AC的中点.连接EG,则在△PAC中易知EC∥PA.又因
PA底面ABCD,故BC底面ABCD.在底面ABCD中,过C作GHBD,垂足为H,连接EH.由三垂线定理知EHBD.从而EHG为二面角E-BD-C的平面角.
设AB=a,则在△PAC中,有
BG=PA=ka.
以下计算GH,考察底面的平面图(如答(19)图2).连结GD.
因S△CBD=BD·GH=GB·OF.
故GH=.
在△ABD中,因为AB=a,AD=2A,得BD=a 第(41)图2
而GB=FB=AD-a.DF-AB,从而得
GH== =
因此tanEHG==
由k>0知是锐角,故要使>,必须
>tan=
解之得,k的取值范围为k>
解法二:
(Ⅰ)如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为:轴建立空间直角坐标系,设AB=a,则易知点A,B,C,D,F的坐标分别为
A(0,0,0),B(a,0,0),C(2a,2a,0),D(0,2a,0),
F(a,2a,0).
从而=(2a,0,0), =(0,2a,0),
·=0,故 .
设PA=b,则P(0,0,b),而E为PC中点.故
E.从而=.
·=0,故.
由此得CD面BEF.
(Ⅱ)设E在xOy平面上的投影为G,过G作GHBD垂足为H,由三垂线定理知EHBD.
从而EHG为二面角E-BD-C的平面角.
由PA=k·AB得P(0,0,ka),E,G(a,a,0).
设H(x,y,0),则=(x-a,y-a,0), =(-a,2a,0),
由·=0得=a(x-a)+2a(y-a)=0,即
x-2y=-a ①
又因=(x,a,y,0),且与的方向相同,故=,即
2x+y=2a ②
由①②解得x=a,y=a,从而=,||=a.
tanEHG===.
由k>0知, EHC是锐角,由EHC>得tanEHG>tan即
>
故k的取值范围为k>.
22. 本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力和推理能力。满分12分
解法一:(Ⅰ)证明:取的中点,连结
∵分别为的中点
∵
∴面,面
∴面面 ∴面
(Ⅱ)设为的中点
∵为的中点 ∴ ∴面
作,交于,连结,则由三垂线定理得
从而为二面角的平面角。
在中,,从而
在中,
故:二面角的大小为
(Ⅲ)
作,交于,由面得
∴面
∴在中,
∴
方法二:以为原点,所在直线分别为轴,轴,轴,建立直角坐标系,则
∵分别是的中点
∴
(Ⅰ)
取,显然面
,∴
又面 ∴面
(Ⅱ)过作,交于,取的中点,则∵
设,则
又
由,及在直线上,可得:
解得
∴ ∴ 即
∴与所夹的角等于二面角的大小
故:二面角的大小为
(Ⅲ)设为平面的法向量,则
又
∴ 即 ∴可取
∴点到平面的距离为
∵,
∴
∴
23.略
24. 解:不妨设正三角形的边长为3,则
(I)在图1中,取BE的中点D,连结DF,
∵AE∶EB=CF∶FA=1∶2,∴AF=AD=2,而∠A=60o,∴△ADF为正三角形。
又AE=DE=1,∴EF⊥AD。
在图2中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的一个平面角,
由题设条件知此二面角为直二面角,∴A1E⊥BE。
又BEEF=E,∴A1E⊥面BEF,即A1E⊥面BEP。
(II)在图2中,∵A1E不垂直于A1B,∴A1E是面A1BP的斜线,又A1E⊥面BEP,∴A1E⊥BP,∴BP垂直于A1E在面A1BP内的射影(三垂线定理的逆定理)
设A1E在面A1BP内的射影为A1Q,且A1Q交BP于Q,
则∠EA1Q就是A1E与面A1BP所成的角,且BP⊥A1Q。
在△EBP中,∵BE=BP=2,∠EBP=60o,∴△EBP为正三角形,∴BE=EP。
又A1E⊥面BEP,∴A1B=A1P,∴Q为BP的中点,且EQ=,而A1E=1,
∴在Rt△A1EQ中,,即直线A1E与面A1BP所成角为60o。
(III)在图3中,过F作FM于M,连结QM、QF。
∵CF=CP=1,∠C=60o,∴△FCP为正三角形,故PF=1,
又PQ=BP=1,∴PF=PQ……①
∵A1E⊥面BEP,EQ=EF=,∴A1F=A1Q,
∴△A1FP△A1QP,故∠A1PF=∠A1PQ……②
由①②及MP为公共边知△FMP△QMP,故∠QMP=∠FMP=90o,且MF=MQ,
∴∠FMQ为二面角B-A1P-F的一个平面角。
在Rt△A1QP中,A1Q=A1F=2,PQ=1,∴A1P=,
∵MQ⊥A1P,∴MQ=,∴MF=。
在△FCQ中,FC=1,QC=2,∠C=60o,由余弦定理得QF=,
在△FMQ中,,
w.w.w.k.s.5.u.c.o.m
www.
α
β
A
B
A′
B′
A
B
C
D
E
F
O
P
第19题图
H
图1
图2
A
B
A1
B1
α
β
l
第20题解法一图
E
F
A
B
A1
B1
α
β
l
第20题解法二图
y
x
y
E
F
图3
Q
M
