2020-2021学年人教版八年级下册第十八章 平行四边形单元提高测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年人教版八年级下册第十八章 平行四边形单元提高测试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 16:10:50 | ||
图片预览


文档简介
第十八章 平行四边形
一、单选题(每题3分,共30分)
1.如图,在平行四边形ABCD中,CE⊥AB,点E为垂足,如果∠D=55°,则
∠BCE=( )
A.55° B.35° C.25° D.30°
1题图 2题图
2.如图在 △ABC中,点D、E分别是AB、A C的中点,BC=6,则DE的长( )
A.2 B.3 C.4 D.5
3.矩形具有而一般平行四边形不一定具有的性质是( )
A.两组对边分别相等 B.两条对角线互相平分
C.两条对角线互相垂直 D.两条对角线相等
4.在平行四边形ABCD中,对角线AC、BD相交于点O,以点O为坐标原点建立平面直角坐标系,其中A(a,b),B(a-1,b+2),C(3,1),则点D的坐标是( )
A.(4,-1) B.(-3,-1) C.(2,3) D.(-4,1)
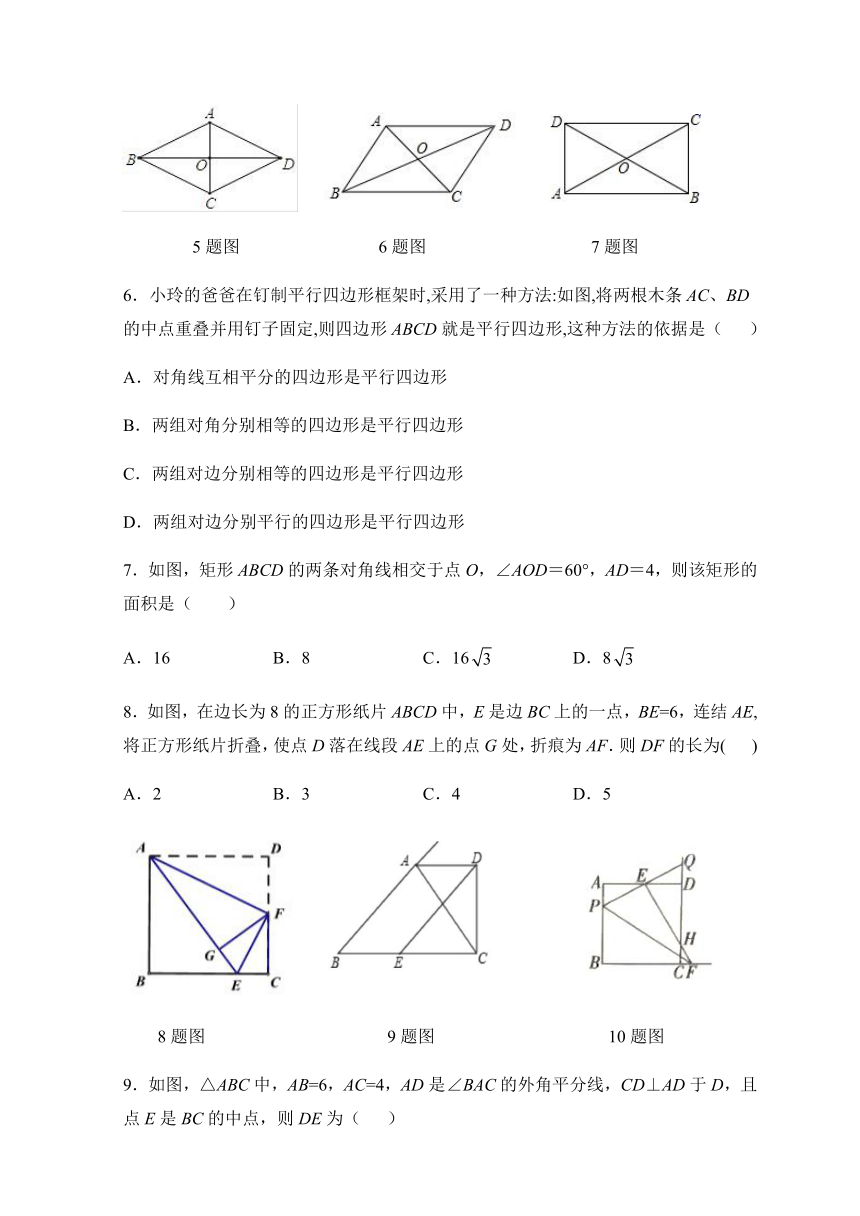
5.如图,在菱形ABCD中,AC与BD相交于点O,AC=6,BD=8,则菱形边长AB等于( )
A.10 B. C.5 D.6
5题图 6题图 7题图
6.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
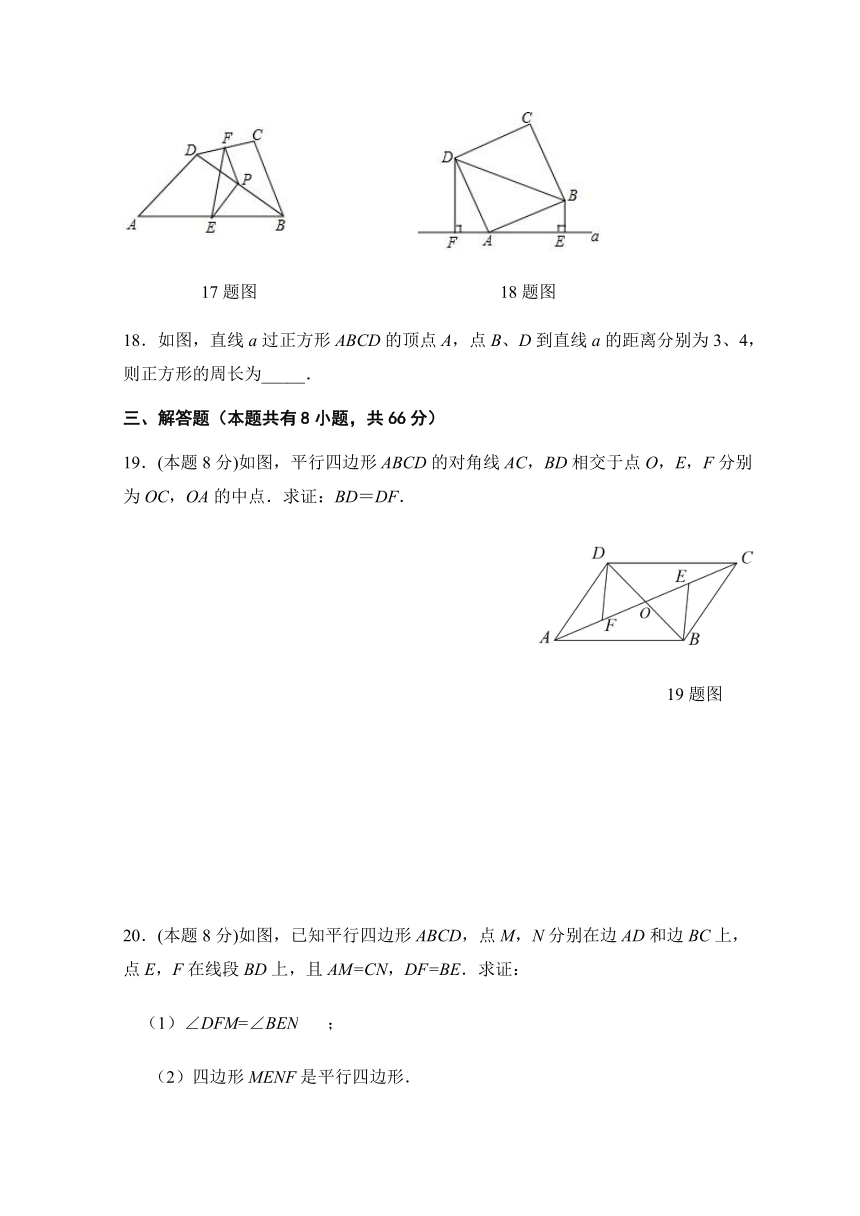
7.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=4,则该矩形的面积是( )
A.16 B.8 C.16 D.8
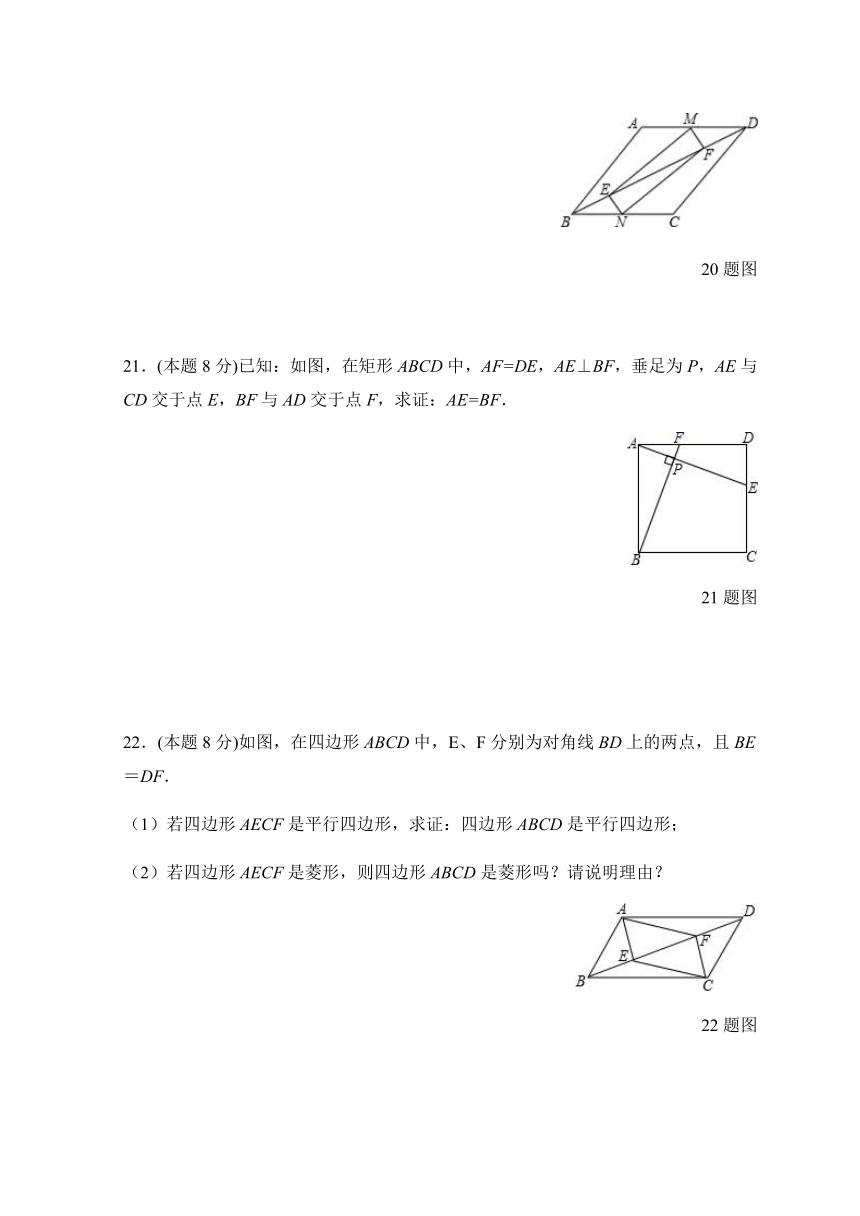
8.如图,在边长为8的正方形纸片ABCD中,E是边BC上的一点,BE=6,连结AE,将正方形纸片折叠,使点D落在线段AE上的点G处,折痕为AF.则DF的长为( )
A.2 B.3 C.4 D.5
8题图 9题图 10题图
9.如图,△ABC中,AB=6,AC=4,AD是∠BAC的外角平分线,CD⊥AD于D,且点E是BC的中点,则DE为( )
A.8.5 B.8 C.7.5 D.5
10.如图,四边形ABCD是边长为2的正方形,点P为线段AB上的动点,E为AD的中点,射线PE交CD的延长线于点Q,过点E作PQ的垂线交CD于点H.交BC的延长线于点F,则以下结论:①∠AEP=∠CHF;②∠EQH=∠CFH;③当点F与点C重合时3PA=PB;④当PA=PB时,CF=2.成立的是( )
A.①②③ B.①③④ C.②③④ D.②④
二、填空题(将正确答案填在题中横线上,每题3分,共24分)
11.已知平行四边形的面积是12cm2,其中一边的长是,则这边上的高是_____cm.
12.一个平行四边形和一个三角形的底相等,它们面积的比是1∶2,它们高的比是__________.
14.正方形的对角线长为1,则正方形的面积为_____________
13.如图,在Rt△ABC中,点D是AB的中点,CD=5,BC=8,则AC=_______.
13题图 15题图 16题图
15.如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2,
则△BDE的面积为_____.
16.如图,在菱形ABCD中,E、F分别是AB、BD的中点,连接EF.如果AB=6,BD=5,那么EF=__________.
17.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是______.
17题图 18题图
18.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为3、4,则正方形的周长为_____.
三、解答题(本题共有8小题,共66分)
19.(本题8分)如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别为OC,OA的中点.求证:BD=DF.
19题图
20.(本题8分)如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
(1)∠DFM=∠BEN;
(2)四边形MENF是平行四边形.
20题图
21.(本题8分)已知:如图,在矩形ABCD中,AF=DE,AE⊥BF,垂足为P,AE与CD交于点E,BF与AD交于点F,求证:AE=BF.
21题图
22.(本题8分)如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,则四边形ABCD是菱形吗?请说明理由?
22题图
23.(本题8分)如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于F,与DC的延长线相交于点H.
(1)求证:△BEF≌△CEH;
(2)求DE的长.
23题图
24.(本题8分)如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
24题图
25.(本题8分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线与BE的延长线相交于点F,连接CF.
(1)求证:四边形CFAD为平行四边形.
(2)若∠BAC=90°,AB=4,BD=,请求出四边形CFAD的面积.
25题图
26.(本题10分)如图,正方形ABCD中,E,F分别为AB,BC中点,CE,DF交于M,CE与DA的延长线相交于点P.
求证:(1)△EBC≌△FCD; (2)CP⊥DF; (3)AM=AD.
26题图
参考答案
1.B. 解析:∵四边形ABCD是平行四边形,∴∠B=∠D=55°,
∵CE⊥AB,∴∠BEC=90°,∴∠BCE=90°-∠B=35°.故选:B.
2.B. 解析:∵点D、E分别是AB、A C的中点,
∴DE为△ABC的中位线,∴DE=BC=3,故选B.
3.D. 解析:A.两组对边分别相等,矩形和平行四边形都具有,故不合题意;
B.两条对角线互相平分,矩形和平行四边形都具有,故不合题意;
C.两条对角线互相垂直,矩形和平行四边形都不一定具有,故不合题意;
D.两条对角线相等,矩形具有而平行四边形不一定具有,符合题意.
故选:D.
4.A. 解析:如图:
∵在?ABCD中,C(3,1),∴A(-3,-1),∴B(-4,1),∴D(4,-1);
故选:A.
5.C. 解析:∵四边形ABCD是菱形,
∴OA=AC,OB=BD,AC⊥BD,
∵AC=6,BD=8,∴OA=3,OB=4,
∴AB==5,即菱形ABCD的边长是5.故选:C.
6.A. 解析:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.故选:A.
7.C. 解析:∵四边形ABCD是矩形,∴OA=OD=OB=OC,
∵∠AOD=60°,∴△AOD是等边三角形,
∴AD=OD=AO=4,∴BD=8,
∴AB=,
∴矩形的面积=4×=,故选:C.
8.C. 解析:∵四边形ABCD是边长为8的正方形纸片,BE=6,
∴AB=BC=CD=DA=8,∠B=∠D=∠C=90°,
∴AE==10,CE=BC?BE=8?6=2,
由翻折可知:
DF=FG,AG=AD=8,∠AGF=∠D=90°,
∴EG=AE?AG=10?8=2,
∵FC=DC?DF=8?DF,
在Rt△FGE和Rt△FCE中,FG2+GE2=FC2+EC2,
∴DF2+22=(8?DF)2+22,解得DF=4,故选:C.
9.D. 解析:延长BA、CD交于F,
∵AD是∠BAC的外角平分线,CD⊥AD,∴AF=AC,CD=DF,
∴BF=BA+AF=BA+AC=10,
∵CD=DF,点E是BC的中点,∴ED= BF=5,故选:D.
10.A. 解析:∵四边形ABCD是正方形,
∴∠ADC= ∠BCD=90°,∴∠DEH +∠DHE=90°,
∵PQ⊥EF,∴∠PEF=∠AEP+∠DEH=90°,∴∠DHE=∠AEP,
∵∠DHE=∠CHF,∴∠AEP=∠CHF,故①正确;
∵∠QEH=∠HCF=90°,∠EHQ=∠CHF,
∴∠EQH=∠CFH,故②正确;
当点F与点C重合时,
∵E是AD的中点,∴AE=ED,
在△PAE和△QDE中,
,
∴△PAE≌△QDE(ASA),∴PE=EQ,PA=DQ,
∵PQ⊥EF,∴PC=QC,
设PA=x,则DQ=x,∴PC=CQ=2+x,PB=2-x,
在Rt△PBC中,,∴,
解得:,∴,∴3PA=PB,故③正确;
∵P是AB中点,∴PA=AE=ED=1,
在Rt△PAE中,∠AEP=45°,
∵∠PEF=90°,∴∠DEH=45°,
在Rt△EDH中,DH=DE=1,∴CH=DH=1,
在△EDH和△FCH中,
,
∴△EDH≌△FCH(ASA),
∴CF=ED=1,故④不正确;
本题成立的结论有①②③;故答案选A.
11.. 解析:设这条边上的高是h,
由题意知,,解得:,故填:.
12.1∶4. 解析:设平行四边形的高为H,三角形的高为h,
则(底×H)︰(底×h÷2)=1︰2,?所以H︰h=1︰4,
答:它们的高的比是1︰4.故答案是:1︰4.
13.6. 解析:在Rt△ABC中,点D是AB的中点,CD=5,
∴AB=2CD=10,又∵BC=8,
∴AC= ,故答案为:6
14.. 解析:∵对角线长为1∴边长为,即面积为=
15.. 解析:∵D、E分别是BC,AD的中点,
∴S△BDE=S△ABD,S△ABD=S△ABC,
∴S△BDE=S△ABC=×6=. 故答案为:.
16.3. 解析:∵四边形ABCD是菱形,∴AB=AD=6,
∵E、F分别是AB、BD的中点,∴EF=AD=3.故答案是:3.
17.120°. 解析:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PE=AD,PF=BC,
∵AD=BC,∴PE=PF,∴△PEF是等腰三角形,
∴∠PFE=∠PEF=30°,∴∠EPF =180°-30°-30°=120°,
故答案为:120°.
18.20. 解析:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°.
∵DF⊥直线m、BE⊥直线m,
∴∠DFA=∠AEB=90°,
∴∠ADF+∠DAF=90°,
∵∠DAF+∠BAE=180°﹣∠BAD=180°﹣90°=90°,
∴∠FDA=∠BAE(同角的余角相等).
∴△DFA≌△AEB(AAS),
∴AF=BE=3,∴AD=,
∴正方形ABCD的周长=4×5=20,
故答案为:20.
19.证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,
∵E、F分别是OC、OA的中点,
∴OE=OC,OF=OA,∴OE=OF.
在△OBE和△ODF中,
OB=OD,∠BOE=∠DOF,OE=OF,
∴△OBE≌△ODF(SAS),∴BE=DF.
20.解:(1)由平行四边形ABCD得AD∥BC,AD=BC,∠ADF=∠CBE,
∵AM=CN,∴AD﹣AM=BC﹣CN,即DM=BN,
又∵DF=BE,∴△DMF≌△BNE(SAS),∴∠DFM=∠BEN;
(2)由△DMF≌△BNE得NE=MF,
∵∠DFM=∠BEN得∠FEN=∠MFE,
∴MF∥NE,∴四边形NEMF是平行四边形;
21.证明:∵四边形ABCD是矩形,AE⊥BF,
∴∠DAE+∠AED=90°,∠DAE+∠AFB=90°,
∴∠AED=∠AFB,
又∵AF=DE,∠BAD=∠D,
∴△AED≌△BFA(ASA),∴AE=BF.
22.(1)证明:连接AC交BD于点O,如图所示:
∵四边形AECF是平行四边形,∴OA=OC,OE=OF,
∵BE=DF,∴BE+OE=DF+OF,∴OB=OD,
∴四边形ABCD是平行四边形;
(2)解:四边形ABCD是菱形,理由如下:
∵四边形AECF是菱形,∴AC⊥BD,
由(1)证四边形ABCD是平行四边形;
∴四边形ABCD是菱形.
23.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∵EF⊥AB,∴EF⊥CD,
∴∠BFE=∠CHE=90°,
∵E是BC的中点,∴BE=CE,
在△BEF和△CEH中,
∠BFE=∠CHE, ∠BEF=∠CEH, BE=CE,
∴△BEF≌△CEH(AAS);
(2)∵∠B=∠HCE=60?,∠BFE=∠H=90?,
∴CH=CE=BC=AD=1,
EH= ,
∴DH=DC+CH=AB+CH=3+1=4 ,
∴在Rt△DEH中, DE= ,
24.(1)∵∠A=∠F,∴DF∥AC,
∵∠DMF=∠1,∠1=∠2,,∴∠DMF=∠2,∴EC∥DB,
∴四边形BCED是平行四边形.
(2)∵BN平分∠DBC,∴∠DBN= ∠CBN,
∵EC∥DB,∴∠CNB=∠DBN,
∴∠BNC=∠NBC,∴CN=BC=DE=2.
25.解:(1)∵E是AD的中点,∴AE=ED,
∵AF∥BC,∴∠AFE=∠DBE,∠FAE=∠BDE,
∴△AFE≌△DBE(AAS),∴AF=BD,
∵AD是BC边中线,∴CD=BD,∴AF=CD,
∴四边形CDAF是平行四边形;
(2)∵∠BAC=90°,AB=4,BD=,AD是BC边上的中线,
∴BC=2BD=5,∴AC=3,
∴S△ACD=S△ABC=S四边形ADCF,
∴四边形CFAD的面积=S△ABC=×3×4=6.
26.证明:(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵E,F分别为AB,BC中点,∴AE=BE=CF=BF,
在△EBC和△FCD中,
,
∴△EBC≌△FCD(SAS);
(2)∵△EBC≌△FCD(SAS),∴∠BCE=∠CDF,
∵∠CDF+∠CFD=90°∴∠BCE+∠CFD=90°,
∴∠CMF=90°,∴CP⊥DF;
(3)∵AD∥BC,∴∠P=∠BCE,
在△APE和△BCE中,
,
∴△APE≌△BCE(AAS),
∴AP=BC,∴AP=AD=PD,
∵DM⊥PM,∴AM=PD,∴AM=AD.
一、单选题(每题3分,共30分)
1.如图,在平行四边形ABCD中,CE⊥AB,点E为垂足,如果∠D=55°,则
∠BCE=( )
A.55° B.35° C.25° D.30°
1题图 2题图
2.如图在 △ABC中,点D、E分别是AB、A C的中点,BC=6,则DE的长( )
A.2 B.3 C.4 D.5
3.矩形具有而一般平行四边形不一定具有的性质是( )
A.两组对边分别相等 B.两条对角线互相平分
C.两条对角线互相垂直 D.两条对角线相等
4.在平行四边形ABCD中,对角线AC、BD相交于点O,以点O为坐标原点建立平面直角坐标系,其中A(a,b),B(a-1,b+2),C(3,1),则点D的坐标是( )
A.(4,-1) B.(-3,-1) C.(2,3) D.(-4,1)
5.如图,在菱形ABCD中,AC与BD相交于点O,AC=6,BD=8,则菱形边长AB等于( )
A.10 B. C.5 D.6
5题图 6题图 7题图
6.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
7.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=4,则该矩形的面积是( )
A.16 B.8 C.16 D.8
8.如图,在边长为8的正方形纸片ABCD中,E是边BC上的一点,BE=6,连结AE,将正方形纸片折叠,使点D落在线段AE上的点G处,折痕为AF.则DF的长为( )
A.2 B.3 C.4 D.5
8题图 9题图 10题图
9.如图,△ABC中,AB=6,AC=4,AD是∠BAC的外角平分线,CD⊥AD于D,且点E是BC的中点,则DE为( )
A.8.5 B.8 C.7.5 D.5
10.如图,四边形ABCD是边长为2的正方形,点P为线段AB上的动点,E为AD的中点,射线PE交CD的延长线于点Q,过点E作PQ的垂线交CD于点H.交BC的延长线于点F,则以下结论:①∠AEP=∠CHF;②∠EQH=∠CFH;③当点F与点C重合时3PA=PB;④当PA=PB时,CF=2.成立的是( )
A.①②③ B.①③④ C.②③④ D.②④
二、填空题(将正确答案填在题中横线上,每题3分,共24分)
11.已知平行四边形的面积是12cm2,其中一边的长是,则这边上的高是_____cm.
12.一个平行四边形和一个三角形的底相等,它们面积的比是1∶2,它们高的比是__________.
14.正方形的对角线长为1,则正方形的面积为_____________
13.如图,在Rt△ABC中,点D是AB的中点,CD=5,BC=8,则AC=_______.
13题图 15题图 16题图
15.如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2,
则△BDE的面积为_____.
16.如图,在菱形ABCD中,E、F分别是AB、BD的中点,连接EF.如果AB=6,BD=5,那么EF=__________.
17.如图,在四边形ABCD中,点P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠PEF=30°,则∠EPF的度数是______.
17题图 18题图
18.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为3、4,则正方形的周长为_____.
三、解答题(本题共有8小题,共66分)
19.(本题8分)如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F分别为OC,OA的中点.求证:BD=DF.
19题图
20.(本题8分)如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
(1)∠DFM=∠BEN;
(2)四边形MENF是平行四边形.
20题图
21.(本题8分)已知:如图,在矩形ABCD中,AF=DE,AE⊥BF,垂足为P,AE与CD交于点E,BF与AD交于点F,求证:AE=BF.
21题图
22.(本题8分)如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,则四边形ABCD是菱形吗?请说明理由?
22题图
23.(本题8分)如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于F,与DC的延长线相交于点H.
(1)求证:△BEF≌△CEH;
(2)求DE的长.
23题图
24.(本题8分)如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
24题图
25.(本题8分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线与BE的延长线相交于点F,连接CF.
(1)求证:四边形CFAD为平行四边形.
(2)若∠BAC=90°,AB=4,BD=,请求出四边形CFAD的面积.
25题图
26.(本题10分)如图,正方形ABCD中,E,F分别为AB,BC中点,CE,DF交于M,CE与DA的延长线相交于点P.
求证:(1)△EBC≌△FCD; (2)CP⊥DF; (3)AM=AD.
26题图
参考答案
1.B. 解析:∵四边形ABCD是平行四边形,∴∠B=∠D=55°,
∵CE⊥AB,∴∠BEC=90°,∴∠BCE=90°-∠B=35°.故选:B.
2.B. 解析:∵点D、E分别是AB、A C的中点,
∴DE为△ABC的中位线,∴DE=BC=3,故选B.
3.D. 解析:A.两组对边分别相等,矩形和平行四边形都具有,故不合题意;
B.两条对角线互相平分,矩形和平行四边形都具有,故不合题意;
C.两条对角线互相垂直,矩形和平行四边形都不一定具有,故不合题意;
D.两条对角线相等,矩形具有而平行四边形不一定具有,符合题意.
故选:D.
4.A. 解析:如图:
∵在?ABCD中,C(3,1),∴A(-3,-1),∴B(-4,1),∴D(4,-1);
故选:A.
5.C. 解析:∵四边形ABCD是菱形,
∴OA=AC,OB=BD,AC⊥BD,
∵AC=6,BD=8,∴OA=3,OB=4,
∴AB==5,即菱形ABCD的边长是5.故选:C.
6.A. 解析:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.故选:A.
7.C. 解析:∵四边形ABCD是矩形,∴OA=OD=OB=OC,
∵∠AOD=60°,∴△AOD是等边三角形,
∴AD=OD=AO=4,∴BD=8,
∴AB=,
∴矩形的面积=4×=,故选:C.
8.C. 解析:∵四边形ABCD是边长为8的正方形纸片,BE=6,
∴AB=BC=CD=DA=8,∠B=∠D=∠C=90°,
∴AE==10,CE=BC?BE=8?6=2,
由翻折可知:
DF=FG,AG=AD=8,∠AGF=∠D=90°,
∴EG=AE?AG=10?8=2,
∵FC=DC?DF=8?DF,
在Rt△FGE和Rt△FCE中,FG2+GE2=FC2+EC2,
∴DF2+22=(8?DF)2+22,解得DF=4,故选:C.
9.D. 解析:延长BA、CD交于F,
∵AD是∠BAC的外角平分线,CD⊥AD,∴AF=AC,CD=DF,
∴BF=BA+AF=BA+AC=10,
∵CD=DF,点E是BC的中点,∴ED= BF=5,故选:D.
10.A. 解析:∵四边形ABCD是正方形,
∴∠ADC= ∠BCD=90°,∴∠DEH +∠DHE=90°,
∵PQ⊥EF,∴∠PEF=∠AEP+∠DEH=90°,∴∠DHE=∠AEP,
∵∠DHE=∠CHF,∴∠AEP=∠CHF,故①正确;
∵∠QEH=∠HCF=90°,∠EHQ=∠CHF,
∴∠EQH=∠CFH,故②正确;
当点F与点C重合时,
∵E是AD的中点,∴AE=ED,
在△PAE和△QDE中,
,
∴△PAE≌△QDE(ASA),∴PE=EQ,PA=DQ,
∵PQ⊥EF,∴PC=QC,
设PA=x,则DQ=x,∴PC=CQ=2+x,PB=2-x,
在Rt△PBC中,,∴,
解得:,∴,∴3PA=PB,故③正确;
∵P是AB中点,∴PA=AE=ED=1,
在Rt△PAE中,∠AEP=45°,
∵∠PEF=90°,∴∠DEH=45°,
在Rt△EDH中,DH=DE=1,∴CH=DH=1,
在△EDH和△FCH中,
,
∴△EDH≌△FCH(ASA),
∴CF=ED=1,故④不正确;
本题成立的结论有①②③;故答案选A.
11.. 解析:设这条边上的高是h,
由题意知,,解得:,故填:.
12.1∶4. 解析:设平行四边形的高为H,三角形的高为h,
则(底×H)︰(底×h÷2)=1︰2,?所以H︰h=1︰4,
答:它们的高的比是1︰4.故答案是:1︰4.
13.6. 解析:在Rt△ABC中,点D是AB的中点,CD=5,
∴AB=2CD=10,又∵BC=8,
∴AC= ,故答案为:6
14.. 解析:∵对角线长为1∴边长为,即面积为=
15.. 解析:∵D、E分别是BC,AD的中点,
∴S△BDE=S△ABD,S△ABD=S△ABC,
∴S△BDE=S△ABC=×6=. 故答案为:.
16.3. 解析:∵四边形ABCD是菱形,∴AB=AD=6,
∵E、F分别是AB、BD的中点,∴EF=AD=3.故答案是:3.
17.120°. 解析:∵点P是对角线BD的中点,点E、F分别是AB、CD的中点,
∴PE=AD,PF=BC,
∵AD=BC,∴PE=PF,∴△PEF是等腰三角形,
∴∠PFE=∠PEF=30°,∴∠EPF =180°-30°-30°=120°,
故答案为:120°.
18.20. 解析:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°.
∵DF⊥直线m、BE⊥直线m,
∴∠DFA=∠AEB=90°,
∴∠ADF+∠DAF=90°,
∵∠DAF+∠BAE=180°﹣∠BAD=180°﹣90°=90°,
∴∠FDA=∠BAE(同角的余角相等).
∴△DFA≌△AEB(AAS),
∴AF=BE=3,∴AD=,
∴正方形ABCD的周长=4×5=20,
故答案为:20.
19.证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,
∵E、F分别是OC、OA的中点,
∴OE=OC,OF=OA,∴OE=OF.
在△OBE和△ODF中,
OB=OD,∠BOE=∠DOF,OE=OF,
∴△OBE≌△ODF(SAS),∴BE=DF.
20.解:(1)由平行四边形ABCD得AD∥BC,AD=BC,∠ADF=∠CBE,
∵AM=CN,∴AD﹣AM=BC﹣CN,即DM=BN,
又∵DF=BE,∴△DMF≌△BNE(SAS),∴∠DFM=∠BEN;
(2)由△DMF≌△BNE得NE=MF,
∵∠DFM=∠BEN得∠FEN=∠MFE,
∴MF∥NE,∴四边形NEMF是平行四边形;
21.证明:∵四边形ABCD是矩形,AE⊥BF,
∴∠DAE+∠AED=90°,∠DAE+∠AFB=90°,
∴∠AED=∠AFB,
又∵AF=DE,∠BAD=∠D,
∴△AED≌△BFA(ASA),∴AE=BF.
22.(1)证明:连接AC交BD于点O,如图所示:
∵四边形AECF是平行四边形,∴OA=OC,OE=OF,
∵BE=DF,∴BE+OE=DF+OF,∴OB=OD,
∴四边形ABCD是平行四边形;
(2)解:四边形ABCD是菱形,理由如下:
∵四边形AECF是菱形,∴AC⊥BD,
由(1)证四边形ABCD是平行四边形;
∴四边形ABCD是菱形.
23.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∵EF⊥AB,∴EF⊥CD,
∴∠BFE=∠CHE=90°,
∵E是BC的中点,∴BE=CE,
在△BEF和△CEH中,
∠BFE=∠CHE, ∠BEF=∠CEH, BE=CE,
∴△BEF≌△CEH(AAS);
(2)∵∠B=∠HCE=60?,∠BFE=∠H=90?,
∴CH=CE=BC=AD=1,
EH= ,
∴DH=DC+CH=AB+CH=3+1=4 ,
∴在Rt△DEH中, DE= ,
24.(1)∵∠A=∠F,∴DF∥AC,
∵∠DMF=∠1,∠1=∠2,,∴∠DMF=∠2,∴EC∥DB,
∴四边形BCED是平行四边形.
(2)∵BN平分∠DBC,∴∠DBN= ∠CBN,
∵EC∥DB,∴∠CNB=∠DBN,
∴∠BNC=∠NBC,∴CN=BC=DE=2.
25.解:(1)∵E是AD的中点,∴AE=ED,
∵AF∥BC,∴∠AFE=∠DBE,∠FAE=∠BDE,
∴△AFE≌△DBE(AAS),∴AF=BD,
∵AD是BC边中线,∴CD=BD,∴AF=CD,
∴四边形CDAF是平行四边形;
(2)∵∠BAC=90°,AB=4,BD=,AD是BC边上的中线,
∴BC=2BD=5,∴AC=3,
∴S△ACD=S△ABC=S四边形ADCF,
∴四边形CFAD的面积=S△ABC=×3×4=6.
26.证明:(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵E,F分别为AB,BC中点,∴AE=BE=CF=BF,
在△EBC和△FCD中,
,
∴△EBC≌△FCD(SAS);
(2)∵△EBC≌△FCD(SAS),∴∠BCE=∠CDF,
∵∠CDF+∠CFD=90°∴∠BCE+∠CFD=90°,
∴∠CMF=90°,∴CP⊥DF;
(3)∵AD∥BC,∴∠P=∠BCE,
在△APE和△BCE中,
,
∴△APE≌△BCE(AAS),
∴AP=BC,∴AP=AD=PD,
∵DM⊥PM,∴AM=PD,∴AM=AD.
