湖南省长沙市师大附中梅溪湖中学2020-2021学年九年级下学期入学考试数学试卷(word版,无答案)
文档属性
| 名称 | 湖南省长沙市师大附中梅溪湖中学2020-2021学年九年级下学期入学考试数学试卷(word版,无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 539.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 00:00:00 | ||
图片预览




文档简介
湖南师大附中梅溪湖中学2020-2021学年第二学期入学测试
九年级
数学
总分:120分,时量:120分钟
一.选择题(本大题共12个小题,每小题3分,共36分.在下列各题的四个选项甲,只有一项是符合题意的.请在答题卡中填涂符合题意的选项)
1.下列实数中,最大的是(
)
A.
B.
C.
D.
2.化简所得的结果是(
)
A.
B.
C.
D.
3.9的算术平方根是(
)
A.
B.3
C.9
D.
4.若,则的值为(
)
A.
B.
C.
D.
5.用配方法解一元二次方程以下正确的是(
)
A.
B.
C.
D.
6.用科学记数法表示0.00000022是(
)
A.
B.
C.
D.
7.如果点和点关于x轴对称,则的值是(
)
A.
B.1
C.
D.5
8.将一块含有角的直角三角板和一把直尺按如图所示方式摆放,若,则的度数是(
)
A.
B.
C.
D.
9.在△中,,,,则的值是(
)
A.
B.
C.
D.
10.若不等式组无解,那么m的取值范围是(
)
A.
B.
C.
D.
11.在平面直角坐标系中,抛物线经平移变换后得到抛物线,则这个变换可以是(
)
A.向左平移2个单位长度
B.向右平移2个单位长度
C.向左平移8个单位长度
D.向右平移8个单位长度
12.如图,矩形中,点在双曲线上,点,在x轴上,延长至点,使,连接交轴于点,连接,则△的面积为(
)
A.5
B.6
C.7
D.8
二.填空题(本大题共4个小题,每小题3分,共12分,请把答案填在题中的横线上)
13.分解因式:
.
14.若,化简
.
15.如图两条相交直线与的图象如图所示,当x
时,.
第12题图
第15题图
第16题图
16.等边△的边长为2,等边△的边长为1,把△放在△中,使与重合,点在边上,如图所示,此时点是中点,在△内部将△按下列方式旋转:绕点顺时针旋转,使点与点重合,完成第1次操作,此时点是中点,△旋转了
°;再绕点顺时针旋转,使点与点重合,完成第2次操作;……这样依次绕△的某个顶点连续旋转下去,第11次操作完成时, .
三.解答题(本大题共8个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题毎小题9分,第24、25题每小題10分,共72分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)计算:
18.(6分)解不等式组,并把它的解集表示在数轴上.
19.(6分)如图,一次函数,与反比例函数交于点、,交轴于点,交x轴于点.
(1)求反比例函数及一次函数的解析式;
(2)求△的面积.
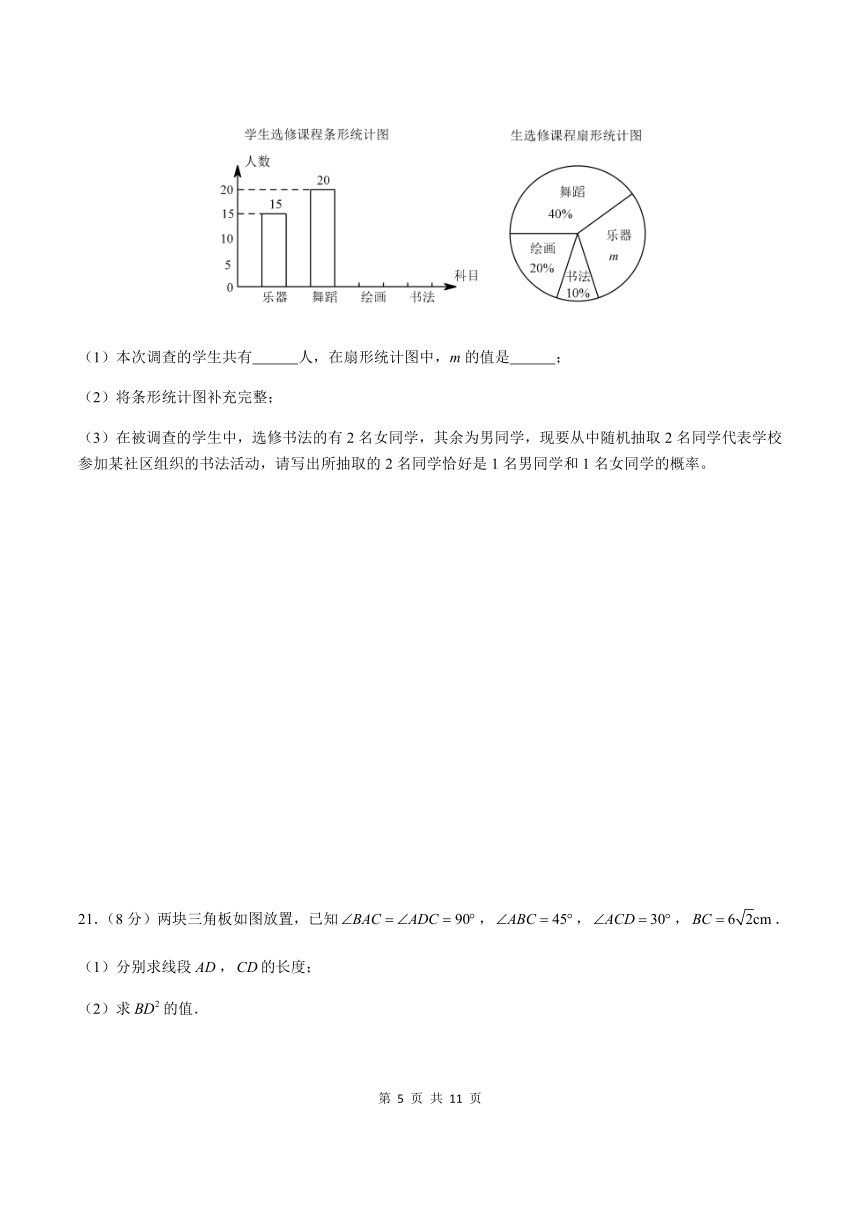
20.(8分)为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)本次调查的学生共有
人,在扇形统计图中,m的值是
;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率。
21.(8分)两块三角板如图放置,已知,,,.
(1)分别求线段,的长度;
(2)求的值.
22.(9分)在抗击“新冠肺炎”战役中,某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务,临时改造了甲、乙两条流水生产线.试产时甲生产线每天的产能(每天的生产的数量)是乙生产线的2倍,各生产80万个,甲比乙少用了2天.
(1)求甲、乙两条生产线每天的产能各是多少?
(2)若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元,要使完成这批任务总运行成本不超过40万元,则至少应安排乙生产线生产多少天?
(3)正式开工满负荷生产3天后,通过技术革新,甲生产线的日产能提高了,乙生产线的日产能翻了一番.再满负荷生产13天能否完成任务?
23.(9分)如图,直线l:与轴交于点,与轴交于点,为线段的一个动点,以为圆心,长为半径作⊙,⊙交于点,连接并延长交⊙于点,连接.
(1)当时,证明:△是等边三角形;
(2)当△△时,求⊙的半径r;
(3)当点在线段上运动时,求的最大值.
24.(10分)有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”.
(1)如图1,平分,,求证:四边形为“和睦四边形”;
(2)如图2,直线与x轴、轴分别交于、两点,点、分别是线段、上的动点.点从点出发,以每秒4个单位长度的速度向点运动.点从点出发,以每秒5个单位长度的速度向点运动.、两点同时出发,设运动时间为t秒.当四边形为“和睦四边形”时,求t的值;
(3)如图3,抛物线(,)与x轴交于、两点(点在点的左侧),与轴交于点,抛物线的顶点为点.当四边形为“和睦四边形”,且.抛物线还满足:顶点在以为直径的圆上.点,是抛物线(,)上任意一点,是否存在△ACD∽△PBD,若存在,请求出点P的坐标;若不存在,请说明理由.
图1
图2
图3
25.(10分)如图,抛物线(其中与x轴分别交于,两点在的右侧),与轴交于点.
(1)请分别求出点A、B、C的坐标(用含的代数式表示)
(2)若点为直线上的一点,且点在第二象限,满足,求的值及用含m的代数式表示点的坐标;
(3)在(2)的情况下,线段与抛物线相交于点,若点恰好为的中点,此时对于在抛物线上且介于点与抛物线顶点之间(含点与顶点)的任意一点,总能使不等式及不等式恒成立,求n的取值范围.
九年级
数学
总分:120分,时量:120分钟
一.选择题(本大题共12个小题,每小题3分,共36分.在下列各题的四个选项甲,只有一项是符合题意的.请在答题卡中填涂符合题意的选项)
1.下列实数中,最大的是(
)
A.
B.
C.
D.
2.化简所得的结果是(
)
A.
B.
C.
D.
3.9的算术平方根是(
)
A.
B.3
C.9
D.
4.若,则的值为(
)
A.
B.
C.
D.
5.用配方法解一元二次方程以下正确的是(
)
A.
B.
C.
D.
6.用科学记数法表示0.00000022是(
)
A.
B.
C.
D.
7.如果点和点关于x轴对称,则的值是(
)
A.
B.1
C.
D.5
8.将一块含有角的直角三角板和一把直尺按如图所示方式摆放,若,则的度数是(
)
A.
B.
C.
D.
9.在△中,,,,则的值是(
)
A.
B.
C.
D.
10.若不等式组无解,那么m的取值范围是(
)
A.
B.
C.
D.
11.在平面直角坐标系中,抛物线经平移变换后得到抛物线,则这个变换可以是(
)
A.向左平移2个单位长度
B.向右平移2个单位长度
C.向左平移8个单位长度
D.向右平移8个单位长度
12.如图,矩形中,点在双曲线上,点,在x轴上,延长至点,使,连接交轴于点,连接,则△的面积为(
)
A.5
B.6
C.7
D.8
二.填空题(本大题共4个小题,每小题3分,共12分,请把答案填在题中的横线上)
13.分解因式:
.
14.若,化简
.
15.如图两条相交直线与的图象如图所示,当x
时,.
第12题图
第15题图
第16题图
16.等边△的边长为2,等边△的边长为1,把△放在△中,使与重合,点在边上,如图所示,此时点是中点,在△内部将△按下列方式旋转:绕点顺时针旋转,使点与点重合,完成第1次操作,此时点是中点,△旋转了
°;再绕点顺时针旋转,使点与点重合,完成第2次操作;……这样依次绕△的某个顶点连续旋转下去,第11次操作完成时, .
三.解答题(本大题共8个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题毎小题9分,第24、25题每小題10分,共72分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)计算:
18.(6分)解不等式组,并把它的解集表示在数轴上.
19.(6分)如图,一次函数,与反比例函数交于点、,交轴于点,交x轴于点.
(1)求反比例函数及一次函数的解析式;
(2)求△的面积.
20.(8分)为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
(1)本次调查的学生共有
人,在扇形统计图中,m的值是
;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率。
21.(8分)两块三角板如图放置,已知,,,.
(1)分别求线段,的长度;
(2)求的值.
22.(9分)在抗击“新冠肺炎”战役中,某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务,临时改造了甲、乙两条流水生产线.试产时甲生产线每天的产能(每天的生产的数量)是乙生产线的2倍,各生产80万个,甲比乙少用了2天.
(1)求甲、乙两条生产线每天的产能各是多少?
(2)若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元,要使完成这批任务总运行成本不超过40万元,则至少应安排乙生产线生产多少天?
(3)正式开工满负荷生产3天后,通过技术革新,甲生产线的日产能提高了,乙生产线的日产能翻了一番.再满负荷生产13天能否完成任务?
23.(9分)如图,直线l:与轴交于点,与轴交于点,为线段的一个动点,以为圆心,长为半径作⊙,⊙交于点,连接并延长交⊙于点,连接.
(1)当时,证明:△是等边三角形;
(2)当△△时,求⊙的半径r;
(3)当点在线段上运动时,求的最大值.
24.(10分)有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”.
(1)如图1,平分,,求证:四边形为“和睦四边形”;
(2)如图2,直线与x轴、轴分别交于、两点,点、分别是线段、上的动点.点从点出发,以每秒4个单位长度的速度向点运动.点从点出发,以每秒5个单位长度的速度向点运动.、两点同时出发,设运动时间为t秒.当四边形为“和睦四边形”时,求t的值;
(3)如图3,抛物线(,)与x轴交于、两点(点在点的左侧),与轴交于点,抛物线的顶点为点.当四边形为“和睦四边形”,且.抛物线还满足:顶点在以为直径的圆上.点,是抛物线(,)上任意一点,是否存在△ACD∽△PBD,若存在,请求出点P的坐标;若不存在,请说明理由.
图1
图2
图3
25.(10分)如图,抛物线(其中与x轴分别交于,两点在的右侧),与轴交于点.
(1)请分别求出点A、B、C的坐标(用含的代数式表示)
(2)若点为直线上的一点,且点在第二象限,满足,求的值及用含m的代数式表示点的坐标;
(3)在(2)的情况下,线段与抛物线相交于点,若点恰好为的中点,此时对于在抛物线上且介于点与抛物线顶点之间(含点与顶点)的任意一点,总能使不等式及不等式恒成立,求n的取值范围.
同课章节目录
