2021年人教版七年级下册5.3《平行线的性质》课时作业(word版,含详解)
文档属性
| 名称 | 2021年人教版七年级下册5.3《平行线的性质》课时作业(word版,含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 124.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 00:00:00 | ||
图片预览




文档简介
2021年人教版七年级下册5.3《平行线的性质》课时作业
一.选择题
1.下列语句中,是命题的是( )
A.正数大于负数 B.作线段AB∥CD
C.连接A、B两点 D.今天的天气好吗
2.下列命题是假命题的是( )
A.对顶角相等
B.两直线平行,内错角相等
C.同位角相等
D.直角三角形两锐角互余
3.如图,已知AB∥DE,∠1=∠2,则AE与DC的位置关系是( )
A.相交 B.垂直 C.平行 D.不能确定
4.如图,下列判断中正确的是( )
A.如果EF∥GH,那么∠4+∠3=180°
B.如果∠1+∠3=180°,那么AB∥CD
C.如果∠2=∠4,那么AB∥CD
D.如果∠1=∠2,那么AB∥CD
5.如图,AB∥CD,∠2是∠1的4倍,则∠2等于( )
A.45° B.90° C.135° D.144°
6.如图,AB∥CD,ME⊥MF,∠EAB=36°,则∠FCD=( )度.
A.51° B.52° C.53° D.54°
7.如图,已知∠BAP与∠APD互补,∠1=∠2,如果∠E=42°,则∠F=( )
A.48° B.42° C.54° D.66°
二.填空题(共6小题)
8.把“不相等的角不是对顶角”改写成“如果…,那么…”的形式是 .
9.如图,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A是135°,则第二次的拐角∠B是 ,根据是 .
10.如图,a∥b,点在直线a上,且AB⊥BC,∠1=30°,那么∠2= .
11.如图,AB∥CD,CE∥GF,若∠1=60°,则∠2= °.
12.如图.将含30°角的直角三角板的直角顶点放在直尺的一边上,已知∠1=35°,则∠2的度数是 °.
13.如图,下列推理:(1)若∠1=∠2,则AB∥CD;(2)若AB∥CD,则∠3=∠4;(3)若∠ABC+∠BCD=180°,则AD∥BC;(4)若∠1=∠2,则∠ADB=∠CBD.其中正确的个数是 个.
三.解答题(共5小题)
14.如图,AC∥FG,∠1=∠2.请问AC与DE平行吗?为什么?
15.如图,已知AB⊥BC,BC⊥CD,BE∥CF,∠ABE=50°,求∠FCD的度数.
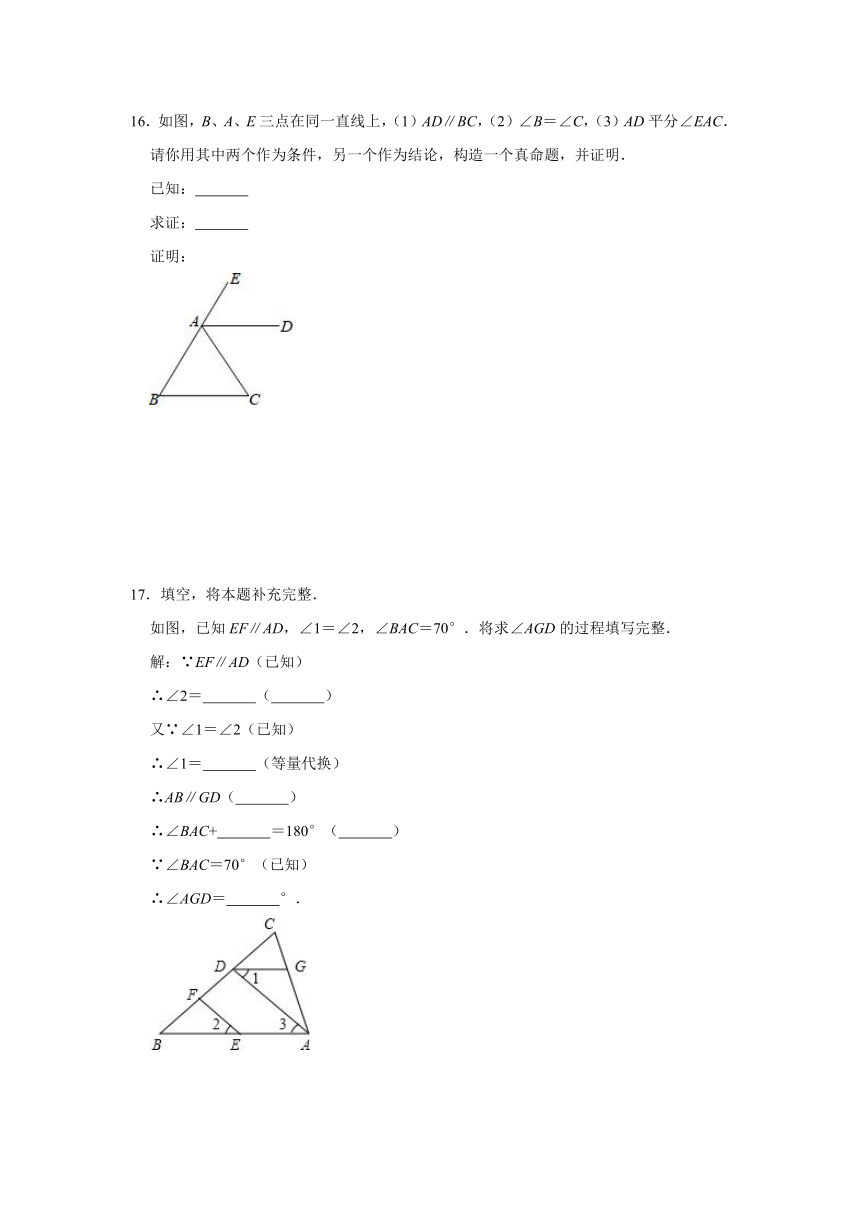
16.如图,B、A、E三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
已知:
求证:
证明:
17.填空,将本题补充完整.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:∵EF∥AD(已知)
∴∠2= ( )
又∵∠1=∠2(已知)
∴∠1= (等量代换)
∴AB∥GD( )
∴∠BAC+ =180°( )
∵∠BAC=70°(已知)
∴∠AGD= °.
18.如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C.
(1)说明CE∥BF;
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
参考答案
一.选择题
1.解:A、正数大于负数是命题,正确;
B、作线段AB∥CD为描述性语言,不是命题,
C、连接A、B两点为描述性语言,不是命题;
D、今天的天气好吗?语句为疑问句,不是命题;
选:A.
2.解:A、对顶角相等,是真命题;
B、两直线平行,内错角相等,是真命题;
C、两直线平行,同位角相等,原命题是假命题;
D、直角三角形两锐角互余,是真命题;
选:C.
3.解:∵AB∥DE,
∴∠1=∠AED,
∵∠1=∠2,
∴∠2=∠AED,
∴AE∥DC.
选:C.
4.解:A、如果EF∥GH,那么∠4+∠3=180°,错误.
B、如果∠1+∠3=180°,那么AB∥CD,错误.
C、如果∠2=∠4,那么AB∥CD,错误.
D、如果∠1=∠2,那么AB∥CD,正确,
选:D.
5.解:如图,
∵AB∥CD,
∴∠1+∠BMN=180°,
∵∠2=∠BMN,
∴∠1+∠2=180°,
∵∠2是∠1的4倍,
∴5∠1=180°,
∴∠1=45°,
∴∠2=135°.
选:C.
6.解:过点M作MN∥AB,
∵AB∥CD,
∴AB∥CD∥MN,
∴∠AMN=∠EAB=36°,
∵ME⊥MF,
∴∠AMC=90°,
∴∠NMC=90°﹣36°=54°,
∴∠FCD=54°.
选:D.
7.解:∵∠BAP+∠APD=180°,
∴AB∥CD,
∴∠BAP=∠APC,
∵∠1=∠2,
∴∠3=∠4,
∴AE∥PF,
∴∠E=∠F=42°,
选:B.
二.填空题(共6小题)
8.解:命题“不相等的角不是对顶角”的题设是两个角不相等,结论为这两个角不是对顶角.
改写成“如果…那…”的形式为:如果两个角不相等,那么这两个角不是对顶角.
答案为:如果两个角不相等,那么这两个角不是对顶角.
9.解:∠B=135°,
理由是:∵道路是平行的,
∴∠B=∠A=135°.
即两直线平行,内错角相等;
答案为:135°;两直线平行,内错角相等
10.解:∵a∥b,∠1=30°,
∴∠3=∠1=30°.
∵AB⊥BC,
∴∠2=90°﹣∠3=60°.
答案为:60°
11.解:∵AB∥CD,
∴∠1=∠CEF,
∵CE∥GF,
∴∠2=∠CEF,
∴∠2=∠1,
∵∠1=60°,
∴∠2=60°,
答案为:60.
12.解:∵a∥b,
∴∠1=∠3=35°,
∴∠2=90°﹣35°=55°,
答案为:55.
13.解:(1)若∠1=∠2,则AD∥BC,(1)不对;
(2)若AB∥CD,则∠3=∠4,(2)正确;
(3)若∠ABC+∠BCD=180°,则AB∥DC,(3)不对;
(4)若∠ABC=∠ADC,∠1=∠2,可推出∠3=∠4,则AB∥CD,(4)正确.
所以有2个正确.
答案为:2.
三.解答题(共5小题)
14.解:AC∥DE,
理由是:∵AC∥FG,
∴∠A=∠2,
∵∠1=∠2,
∴∠A=∠1,
∴AC∥DE.
15.解:∵AB⊥BC,BC⊥CD,
∴AB∥CD,
∴∠ABC=∠DCB,
∵BE∥CF,
∴∠EBC=∠FCB,
∴∠ABE=∠DCF,
又∵∠ABE=50°,
∴∠FCD=50°.
16.解:命题:已知:AD∥BC,∠B=∠C,
求证:AD平分∠EAC.
证明:∵AD∥BC,
∴∠B=∠EAD,∠C=∠DAC.
又∵∠B=∠C,
∴∠EAD=∠DAC.
即AD平分∠EAC.
是真命题.
答案为:AD∥BC,∠B=∠C,AD平分∠EAC.
17.解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴AB∥GD(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
∵∠BAC=70°(已知)
∴∠AGD=110°.
答案为∠3;两直线平行,同位角相等;∠3;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°
18.解:(1)∵∠1=∠4,∠1=∠2,
∴∠2=∠4,
∴CE∥BF;
(2)∠B=∠3,∠A=∠D成立.
∵由(1)得,CE∥BF,
∴∠3=∠C.
∵∠B=∠C,
∴∠B=∠3,
∴AB∥CD,
∴∠A=∠D.
一.选择题
1.下列语句中,是命题的是( )
A.正数大于负数 B.作线段AB∥CD
C.连接A、B两点 D.今天的天气好吗
2.下列命题是假命题的是( )
A.对顶角相等
B.两直线平行,内错角相等
C.同位角相等
D.直角三角形两锐角互余
3.如图,已知AB∥DE,∠1=∠2,则AE与DC的位置关系是( )
A.相交 B.垂直 C.平行 D.不能确定
4.如图,下列判断中正确的是( )
A.如果EF∥GH,那么∠4+∠3=180°
B.如果∠1+∠3=180°,那么AB∥CD
C.如果∠2=∠4,那么AB∥CD
D.如果∠1=∠2,那么AB∥CD
5.如图,AB∥CD,∠2是∠1的4倍,则∠2等于( )
A.45° B.90° C.135° D.144°
6.如图,AB∥CD,ME⊥MF,∠EAB=36°,则∠FCD=( )度.
A.51° B.52° C.53° D.54°
7.如图,已知∠BAP与∠APD互补,∠1=∠2,如果∠E=42°,则∠F=( )
A.48° B.42° C.54° D.66°
二.填空题(共6小题)
8.把“不相等的角不是对顶角”改写成“如果…,那么…”的形式是 .
9.如图,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A是135°,则第二次的拐角∠B是 ,根据是 .
10.如图,a∥b,点在直线a上,且AB⊥BC,∠1=30°,那么∠2= .
11.如图,AB∥CD,CE∥GF,若∠1=60°,则∠2= °.
12.如图.将含30°角的直角三角板的直角顶点放在直尺的一边上,已知∠1=35°,则∠2的度数是 °.
13.如图,下列推理:(1)若∠1=∠2,则AB∥CD;(2)若AB∥CD,则∠3=∠4;(3)若∠ABC+∠BCD=180°,则AD∥BC;(4)若∠1=∠2,则∠ADB=∠CBD.其中正确的个数是 个.
三.解答题(共5小题)
14.如图,AC∥FG,∠1=∠2.请问AC与DE平行吗?为什么?
15.如图,已知AB⊥BC,BC⊥CD,BE∥CF,∠ABE=50°,求∠FCD的度数.
16.如图,B、A、E三点在同一直线上,(1)AD∥BC,(2)∠B=∠C,(3)AD平分∠EAC.
请你用其中两个作为条件,另一个作为结论,构造一个真命题,并证明.
已知:
求证:
证明:
17.填空,将本题补充完整.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:∵EF∥AD(已知)
∴∠2= ( )
又∵∠1=∠2(已知)
∴∠1= (等量代换)
∴AB∥GD( )
∴∠BAC+ =180°( )
∵∠BAC=70°(已知)
∴∠AGD= °.
18.如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C.
(1)说明CE∥BF;
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
参考答案
一.选择题
1.解:A、正数大于负数是命题,正确;
B、作线段AB∥CD为描述性语言,不是命题,
C、连接A、B两点为描述性语言,不是命题;
D、今天的天气好吗?语句为疑问句,不是命题;
选:A.
2.解:A、对顶角相等,是真命题;
B、两直线平行,内错角相等,是真命题;
C、两直线平行,同位角相等,原命题是假命题;
D、直角三角形两锐角互余,是真命题;
选:C.
3.解:∵AB∥DE,
∴∠1=∠AED,
∵∠1=∠2,
∴∠2=∠AED,
∴AE∥DC.
选:C.
4.解:A、如果EF∥GH,那么∠4+∠3=180°,错误.
B、如果∠1+∠3=180°,那么AB∥CD,错误.
C、如果∠2=∠4,那么AB∥CD,错误.
D、如果∠1=∠2,那么AB∥CD,正确,
选:D.
5.解:如图,
∵AB∥CD,
∴∠1+∠BMN=180°,
∵∠2=∠BMN,
∴∠1+∠2=180°,
∵∠2是∠1的4倍,
∴5∠1=180°,
∴∠1=45°,
∴∠2=135°.
选:C.
6.解:过点M作MN∥AB,
∵AB∥CD,
∴AB∥CD∥MN,
∴∠AMN=∠EAB=36°,
∵ME⊥MF,
∴∠AMC=90°,
∴∠NMC=90°﹣36°=54°,
∴∠FCD=54°.
选:D.
7.解:∵∠BAP+∠APD=180°,
∴AB∥CD,
∴∠BAP=∠APC,
∵∠1=∠2,
∴∠3=∠4,
∴AE∥PF,
∴∠E=∠F=42°,
选:B.
二.填空题(共6小题)
8.解:命题“不相等的角不是对顶角”的题设是两个角不相等,结论为这两个角不是对顶角.
改写成“如果…那…”的形式为:如果两个角不相等,那么这两个角不是对顶角.
答案为:如果两个角不相等,那么这两个角不是对顶角.
9.解:∠B=135°,
理由是:∵道路是平行的,
∴∠B=∠A=135°.
即两直线平行,内错角相等;
答案为:135°;两直线平行,内错角相等
10.解:∵a∥b,∠1=30°,
∴∠3=∠1=30°.
∵AB⊥BC,
∴∠2=90°﹣∠3=60°.
答案为:60°
11.解:∵AB∥CD,
∴∠1=∠CEF,
∵CE∥GF,
∴∠2=∠CEF,
∴∠2=∠1,
∵∠1=60°,
∴∠2=60°,
答案为:60.
12.解:∵a∥b,
∴∠1=∠3=35°,
∴∠2=90°﹣35°=55°,
答案为:55.
13.解:(1)若∠1=∠2,则AD∥BC,(1)不对;
(2)若AB∥CD,则∠3=∠4,(2)正确;
(3)若∠ABC+∠BCD=180°,则AB∥DC,(3)不对;
(4)若∠ABC=∠ADC,∠1=∠2,可推出∠3=∠4,则AB∥CD,(4)正确.
所以有2个正确.
答案为:2.
三.解答题(共5小题)
14.解:AC∥DE,
理由是:∵AC∥FG,
∴∠A=∠2,
∵∠1=∠2,
∴∠A=∠1,
∴AC∥DE.
15.解:∵AB⊥BC,BC⊥CD,
∴AB∥CD,
∴∠ABC=∠DCB,
∵BE∥CF,
∴∠EBC=∠FCB,
∴∠ABE=∠DCF,
又∵∠ABE=50°,
∴∠FCD=50°.
16.解:命题:已知:AD∥BC,∠B=∠C,
求证:AD平分∠EAC.
证明:∵AD∥BC,
∴∠B=∠EAD,∠C=∠DAC.
又∵∠B=∠C,
∴∠EAD=∠DAC.
即AD平分∠EAC.
是真命题.
答案为:AD∥BC,∠B=∠C,AD平分∠EAC.
17.解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴AB∥GD(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
∵∠BAC=70°(已知)
∴∠AGD=110°.
答案为∠3;两直线平行,同位角相等;∠3;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°
18.解:(1)∵∠1=∠4,∠1=∠2,
∴∠2=∠4,
∴CE∥BF;
(2)∠B=∠3,∠A=∠D成立.
∵由(1)得,CE∥BF,
∴∠3=∠C.
∵∠B=∠C,
∴∠B=∠3,
∴AB∥CD,
∴∠A=∠D.
