人教版八年级数学下册:17.1勾股定理练习(word版,含答案)
文档属性
| 名称 | 人教版八年级数学下册:17.1勾股定理练习(word版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 370.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-02 00:00:00 | ||
图片预览

文档简介
直角三角形勾股定理练习
一、选择题
1.
一个直角三角形两边长分别是3和4,则第三边长是??(????)
A.
5?????????????B.
?????????????C.
5或?????????????D.
2?????????????
2.
如图,每个小正方形的边长为1,△ABC的三边a,b,c的大小关系式为??(????)
?
A.
aacc3.
如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为(????)
?
A.
?????????????B.
?????????????C.
4?????????????D.
5?????????????
4.
如图,有一块直角三角形纸片,两直角边AC=6?cm,BC=8?cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于??(????)
?
A.
2?cm?????????????B.
3?cm?????????????C.
4?cm?????????????D.
5?cm?????????????
5.
如图,在△ABC中,∠ACB=90°,AC=40,CB=9,点M,N在AB上,且AM=AC,BN=BC,则MN的长为??(????)
?
A.
6?????????????B.
7?????????????C.
8?????????????D.
9?????????????
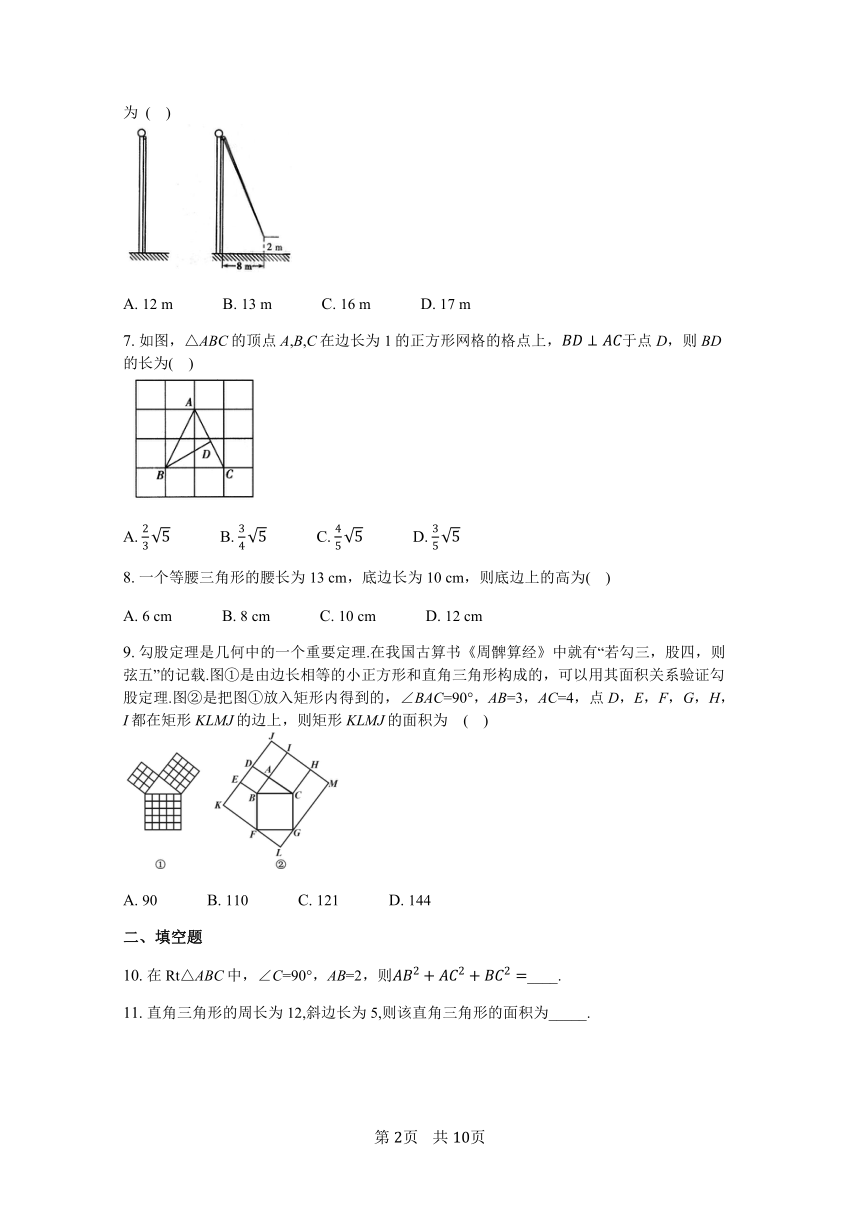
6.
如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8?m处,发现此时绳子末端距离地面2?m,则旗杆的高度(滑轮上方的部分忽略不计)为??(????)
?
A.
12?m?????????????B.
13?m?????????????C.
16?m?????????????D.
17?m?????????????
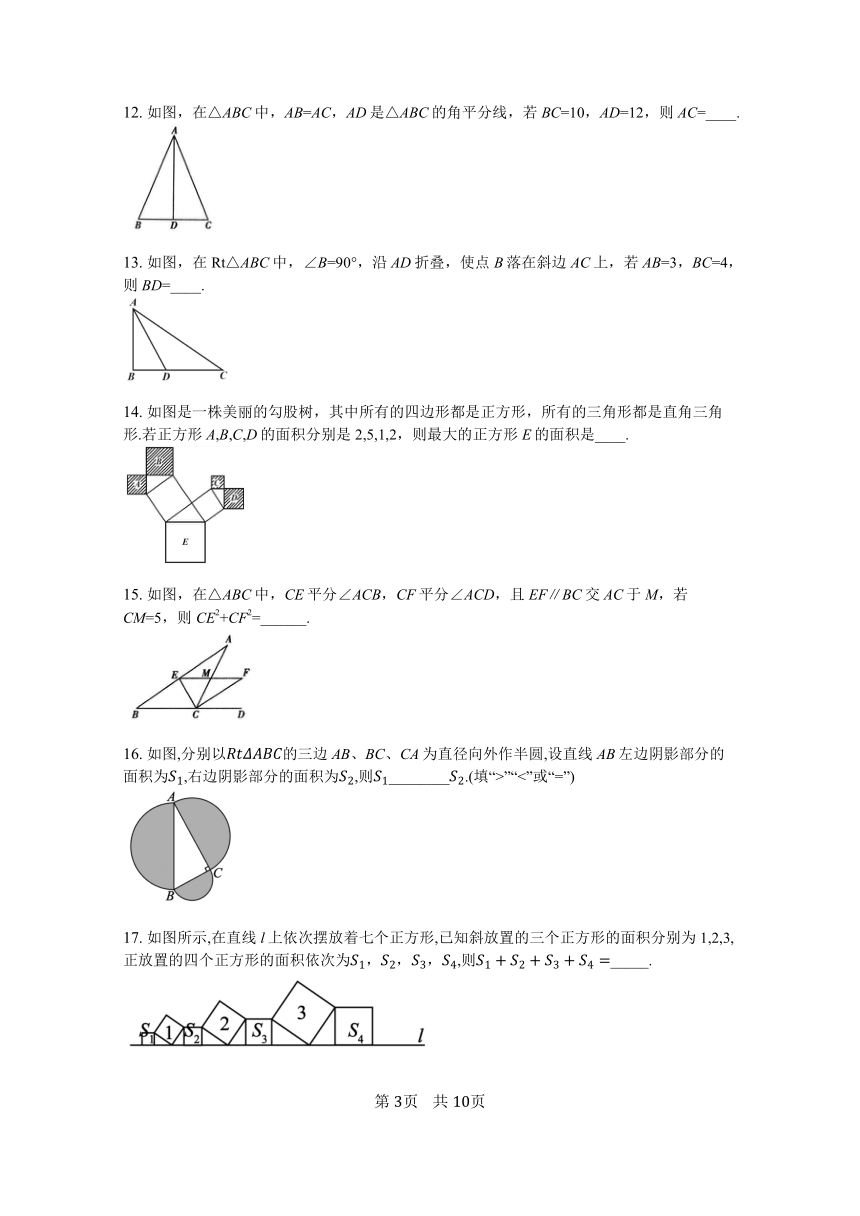
7.
如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,于点D,则BD的长为(????)
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
8.
一个等腰三角形的腰长为13?cm,底边长为10?cm,则底边上的高为(????)
A.
6?cm?????????????B.
8?cm?????????????C.
10?cm?????????????D.
12?cm?????????????
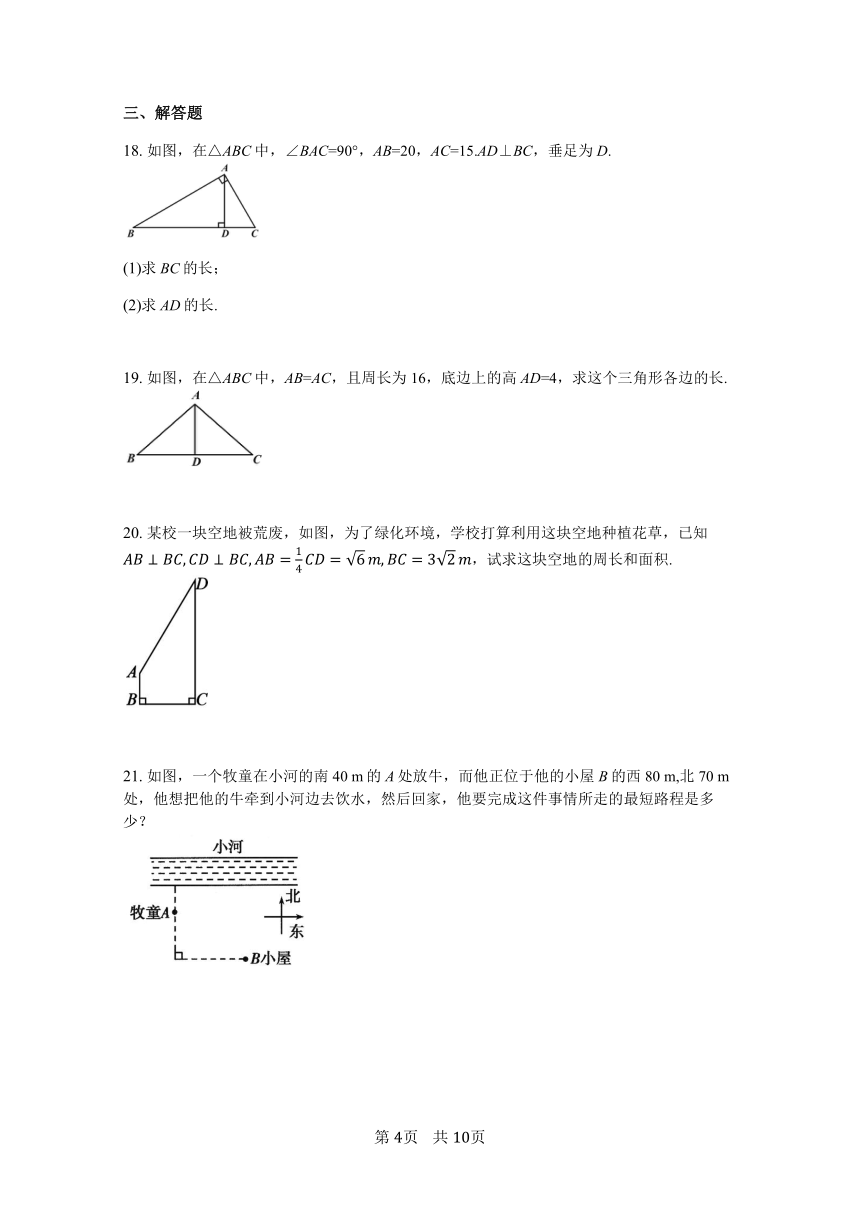
9.
勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是把图①放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为????(????)
?
A.
90?????????????B.
110?????????????C.
121?????????????D.
144?????????????
二、填空题
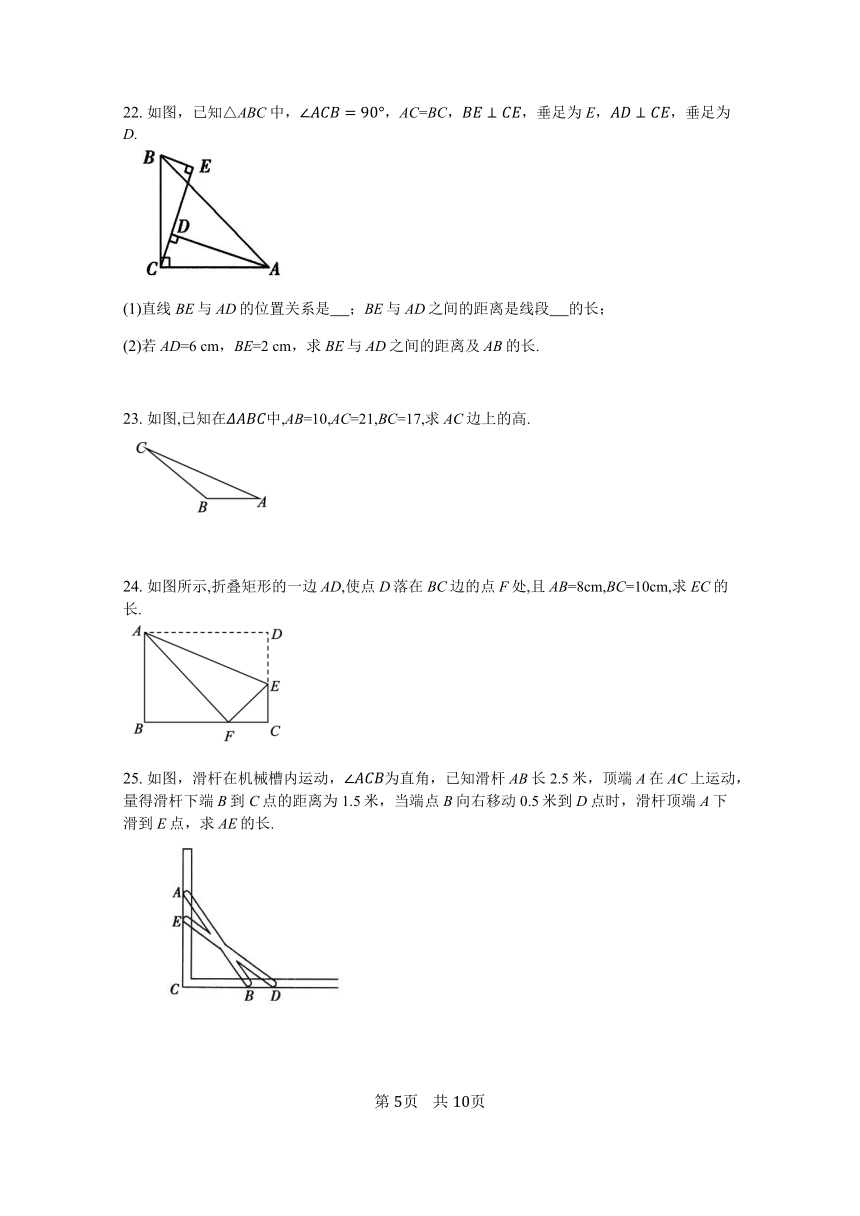
10.
在Rt△ABC中,∠C=90°,AB=2,则____.
11.
直角三角形的周长为12,斜边长为5,则该直角三角形的面积为_____.
12.
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,若BC=10,AD=12,则AC=____.
?
13.
如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上,若AB=3,BC=4,则BD=____.
?
14.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的面积分别是2,5,1,2,则最大的正方形E的面积是____.
?
15.
如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2=______.
?
16.
如图,分别以的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分的面积为,右边阴影部分的面积为,则________.(填“>”“<”或“=”)
?
17.
如图所示,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积依次为,,,,则_____.
?
三、解答题
18.
如图,在△ABC中,∠BAC=90°,AB=20,AC=15.AD⊥BC,垂足为D.
?
(1)求BC的长;
(2)求AD的长.
19.
如图,在△ABC中,AB=AC,且周长为16,底边上的高AD=4,求这个三角形各边的长.
?
20.
某校一块空地被荒废,如图,为了绿化环境,学校打算利用这块空地种植花草,已知,试求这块空地的周长和面积.
?
21.
如图,一个牧童在小河的南40?m的A处放牛,而他正位于他的小屋B的西80?m,北70?m处,他想把他的牛牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少??
?
22.
如图,已知△ABC中,,AC=BC,,垂足为E,,垂足为D.
?
(1)直线BE与AD的位置关系是?????;BE与AD之间的距离是线段?????的长;
(2)若AD=6?cm,BE=2?cm,求BE与AD之间的距离及AB的长.
23.
如图,已知在中,AB=10,AC=21,BC=17,求AC边上的高.
?
24.
如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,且AB=8cm,BC=10cm,求EC的长.
?
25.
如图,滑杆在机械槽内运动,为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B到C点的距离为1.5米,当端点B向右移动0.5米到D点时,滑杆顶端A下滑到E点,求AE的长.
?
参考答案
1.
【答案】C【解析】分两种情况讨论,当4为斜边,第三边为,
?当4为直角边,第三边为,故选C.
2.
【答案】C【解析】由网格可得:把a,b分别看作网格中两个直角三角形的斜边,再根据勾股定理计算:
?,∴c3.
【答案】C【解析】设BN=x,则AN=9-x,
?由折叠可得DN=AN=9-x,
?∵D是BC的中点,BC=6,∴BD=3.
?在Rt△BND中,,解得x=4.
?故线段BN的长为4.故选C.
4.
【答案】B【解析】在Rt△ABC中,AC=6?cm,BC=8?cm,根据勾股定理得:AB=10?cm,
?根据折叠性质得:DE⊥AB,CD=DE,AE=AC=6?cm,∴BE=10-6=4(cm),
?设CD的长为xcm,则BD=(8-x)cm,
?在Rt△BED中,BD2=DE2+BE2,即,解得x=3,即CD的长为3?cm,故选B.
5.
【答案】C【解析】在Rt△ABC中,因为AC=40,BC=9,所以由勾股定理得AB=,
?因为AM=AC,所以BM=AB-AM=41-40=1,因为BN=BC=9,所以MN=BN-BM=9-1=8,故选C.
6.
【答案】D【解析】如图所示,作BC⊥AE于点C,
?因为四边形BDEC为矩形,所以BC=DE=8,
?设AE=x,则AB=x,AC=x-2,
?在Rt△ABC中,根据勾股定理得AC2+BC2=AB2,即(x-2)2+82=x2,解得x=17.
?即旗杆的高度为17?m,故选D.
?
7.
【答案】C【解析】由勾股定理得.
?∵,即,∴,故选C.
8.
【答案】D【解析】如图,AB=AC=13?cm,BC=10?cm,作于D,则,在Rt△ABD中,由勾股定理得,∴AD=12?cm.故选D.
?
9.
【答案】B【解析】延长AB与KL相交于N,延长AC与ML相交于Q,易证△ABC≌△QCG≌△LGF≌△NFB,全等三角形对应边相等,则ML=3+4+4=11,KL=3+4+3=10,所以矩形KLMJ的面积为11×10=110,故选B.
?
10.
【答案】8
?【解析】因为∠C=90°,所以AB为斜边,
?由勾股定理得,所以.
11.
【答案】6
?【解析】设此直角三角形的两直角边长为a、b,因为周长为12,斜边长为5,则,又由勾股定理知,∴,则,故其面积为.
12.
【答案】13
?【解析】∵AB=AC,AD是△ABC的角平分线,
?根据三线合一得:AD⊥BC,BD=DC,
?在Rt△ADC中,.
13.
【答案】
?【解析】设点B落在斜边AC上的B′处,连接DB′,则DB?′=DB.
?因为∠B=90°,由勾股定理得AC=5,
?因为△ABD与△AB′D重合,所以AB?′=AB,所以B′C=5-3=2,
?设DB=x,则DC=4-x,由折叠知∠CB′D=90°,
?在Rt△DB′C中,利用勾股定理得,解得,所以.
?
14.
【答案】10
?【解析】设正方形A,B的边长分别为a,b,中间两个正方形的边长分别为x,y,最大正方形E的边长为z,
?则由勾股定理得,因为a?=2,b?=5,所以x?=7,即空白正方形的面积等于正方形A,B的面积之和.
?同理,y?=3,z?=x?+y?=10,即最大正方形E的面积为10.
15.
【答案】100
?【解析】因为CE平分∠ACB,CF平分∠ACD,∠ACB+∠ACD=180°,所以∠ECF=90°,
?因为CE平分∠ACB,所以∠BCE=∠MCE,因为EF∥BC,所以∠CEM=∠BCE,
?所以∠CEM=∠MCE,所以ME=MC,
?同理可得∠MCF=∠MFC,所以EM=MC=MF=5,所以EF=10,
?在Rt△CEF中,由勾股定理可得CE2+CF2=EF2=100.
16.
【答案】=
?【解析】图中阴影部分的面积是以的三边AB、BC、CA为直径向外作的半圆,∴,,又∵在中,,三边满足勾股定理,则∴.
17.
【答案】4
?【解析】由图易证,最左端斜放置的正方形与相邻两个正方形所夹的两个直角三角形是两个全等的三角形,则易得.同理可证,∴.
18.(1)
【答案】因为∠BAC=90°,由勾股定理得.
?(2)
【答案】由三角形的面积得:,得,则AD=12.
?
19.
【答案】设BD=x,∵AD是底边BC上的高,AB=AC,∴,所以BC=2x,
?∵△ABC的周长为16,∴,∴AB=8-x,
?在Rt△ABD中,,即,解得x=3,
?∴AB=8-3=5,BC=2BD=2×3=6,
?∴△ABC的边AB,AC的长均为5,边BC的长为6.
?
20.
【答案】过点作,垂足为点.
?,,
?.
?空地的周长为.
?空地的面积为.
21.
【答案】如图,作出A点关于MN的对称点,连接交MN于点P,则的长就是最短路线的长,
?
?在中,由勾股定理求得.
?答:他要完成这件事情所走的最短路程是170?m.
?
22.(1)
【答案】平行;ED.
?(2)
【答案】∵,,
?∴与互余,与互余,∴,
?∵AC=BC,,
?∴,∴EC=AD,BE=CD,
?∴BE与AD之间的距离ED=EC-CD=AD-BE=6-2=4(cm).
?又∵,
?∴.
?
23.
【答案】过点B作于点D.设AD=x,则CD=21-x.
?
?在中,
?在中,
?∴,解得x=6,∴,∴BD=8.
?即AC边上的高为8.
?
24.
【答案】设DE=x,则EF=x,EC=8-x.在中,∵AD=AF=10,由勾股定理,得BF=6,∴FC=4.在中,由勾股定理,得,∴,∴x=5,即EC的长为3cm.
?
25.
【答案】由题意得AB=DE=2.5米,,
?在Rt△ABC中,根据勾股定理,得AC=2米.
?在Rt△CED中,根据勾股定理,得CE=1.5米,
?所以AE=2-1.5=0.5米,即AE的长为0.5米.
?
第10页
共10页
第9页
共10页
一、选择题
1.
一个直角三角形两边长分别是3和4,则第三边长是??(????)
A.
5?????????????B.
?????????????C.
5或?????????????D.
2?????????????
2.
如图,每个小正方形的边长为1,△ABC的三边a,b,c的大小关系式为??(????)
?
A.
a
如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为(????)
?
A.
?????????????B.
?????????????C.
4?????????????D.
5?????????????
4.
如图,有一块直角三角形纸片,两直角边AC=6?cm,BC=8?cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于??(????)
?
A.
2?cm?????????????B.
3?cm?????????????C.
4?cm?????????????D.
5?cm?????????????
5.
如图,在△ABC中,∠ACB=90°,AC=40,CB=9,点M,N在AB上,且AM=AC,BN=BC,则MN的长为??(????)
?
A.
6?????????????B.
7?????????????C.
8?????????????D.
9?????????????
6.
如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8?m处,发现此时绳子末端距离地面2?m,则旗杆的高度(滑轮上方的部分忽略不计)为??(????)
?
A.
12?m?????????????B.
13?m?????????????C.
16?m?????????????D.
17?m?????????????
7.
如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,于点D,则BD的长为(????)
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
8.
一个等腰三角形的腰长为13?cm,底边长为10?cm,则底边上的高为(????)
A.
6?cm?????????????B.
8?cm?????????????C.
10?cm?????????????D.
12?cm?????????????
9.
勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.图①是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图②是把图①放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为????(????)
?
A.
90?????????????B.
110?????????????C.
121?????????????D.
144?????????????
二、填空题
10.
在Rt△ABC中,∠C=90°,AB=2,则____.
11.
直角三角形的周长为12,斜边长为5,则该直角三角形的面积为_____.
12.
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,若BC=10,AD=12,则AC=____.
?
13.
如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC上,若AB=3,BC=4,则BD=____.
?
14.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的面积分别是2,5,1,2,则最大的正方形E的面积是____.
?
15.
如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2=______.
?
16.
如图,分别以的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分的面积为,右边阴影部分的面积为,则________.(填“>”“<”或“=”)
?
17.
如图所示,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积依次为,,,,则_____.
?
三、解答题
18.
如图,在△ABC中,∠BAC=90°,AB=20,AC=15.AD⊥BC,垂足为D.
?
(1)求BC的长;
(2)求AD的长.
19.
如图,在△ABC中,AB=AC,且周长为16,底边上的高AD=4,求这个三角形各边的长.
?
20.
某校一块空地被荒废,如图,为了绿化环境,学校打算利用这块空地种植花草,已知,试求这块空地的周长和面积.
?
21.
如图,一个牧童在小河的南40?m的A处放牛,而他正位于他的小屋B的西80?m,北70?m处,他想把他的牛牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少??
?
22.
如图,已知△ABC中,,AC=BC,,垂足为E,,垂足为D.
?
(1)直线BE与AD的位置关系是?????;BE与AD之间的距离是线段?????的长;
(2)若AD=6?cm,BE=2?cm,求BE与AD之间的距离及AB的长.
23.
如图,已知在中,AB=10,AC=21,BC=17,求AC边上的高.
?
24.
如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,且AB=8cm,BC=10cm,求EC的长.
?
25.
如图,滑杆在机械槽内运动,为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B到C点的距离为1.5米,当端点B向右移动0.5米到D点时,滑杆顶端A下滑到E点,求AE的长.
?
参考答案
1.
【答案】C【解析】分两种情况讨论,当4为斜边,第三边为,
?当4为直角边,第三边为,故选C.
2.
【答案】C【解析】由网格可得:把a,b分别看作网格中两个直角三角形的斜边,再根据勾股定理计算:
?,∴c
【答案】C【解析】设BN=x,则AN=9-x,
?由折叠可得DN=AN=9-x,
?∵D是BC的中点,BC=6,∴BD=3.
?在Rt△BND中,,解得x=4.
?故线段BN的长为4.故选C.
4.
【答案】B【解析】在Rt△ABC中,AC=6?cm,BC=8?cm,根据勾股定理得:AB=10?cm,
?根据折叠性质得:DE⊥AB,CD=DE,AE=AC=6?cm,∴BE=10-6=4(cm),
?设CD的长为xcm,则BD=(8-x)cm,
?在Rt△BED中,BD2=DE2+BE2,即,解得x=3,即CD的长为3?cm,故选B.
5.
【答案】C【解析】在Rt△ABC中,因为AC=40,BC=9,所以由勾股定理得AB=,
?因为AM=AC,所以BM=AB-AM=41-40=1,因为BN=BC=9,所以MN=BN-BM=9-1=8,故选C.
6.
【答案】D【解析】如图所示,作BC⊥AE于点C,
?因为四边形BDEC为矩形,所以BC=DE=8,
?设AE=x,则AB=x,AC=x-2,
?在Rt△ABC中,根据勾股定理得AC2+BC2=AB2,即(x-2)2+82=x2,解得x=17.
?即旗杆的高度为17?m,故选D.
?
7.
【答案】C【解析】由勾股定理得.
?∵,即,∴,故选C.
8.
【答案】D【解析】如图,AB=AC=13?cm,BC=10?cm,作于D,则,在Rt△ABD中,由勾股定理得,∴AD=12?cm.故选D.
?
9.
【答案】B【解析】延长AB与KL相交于N,延长AC与ML相交于Q,易证△ABC≌△QCG≌△LGF≌△NFB,全等三角形对应边相等,则ML=3+4+4=11,KL=3+4+3=10,所以矩形KLMJ的面积为11×10=110,故选B.
?
10.
【答案】8
?【解析】因为∠C=90°,所以AB为斜边,
?由勾股定理得,所以.
11.
【答案】6
?【解析】设此直角三角形的两直角边长为a、b,因为周长为12,斜边长为5,则,又由勾股定理知,∴,则,故其面积为.
12.
【答案】13
?【解析】∵AB=AC,AD是△ABC的角平分线,
?根据三线合一得:AD⊥BC,BD=DC,
?在Rt△ADC中,.
13.
【答案】
?【解析】设点B落在斜边AC上的B′处,连接DB′,则DB?′=DB.
?因为∠B=90°,由勾股定理得AC=5,
?因为△ABD与△AB′D重合,所以AB?′=AB,所以B′C=5-3=2,
?设DB=x,则DC=4-x,由折叠知∠CB′D=90°,
?在Rt△DB′C中,利用勾股定理得,解得,所以.
?
14.
【答案】10
?【解析】设正方形A,B的边长分别为a,b,中间两个正方形的边长分别为x,y,最大正方形E的边长为z,
?则由勾股定理得,因为a?=2,b?=5,所以x?=7,即空白正方形的面积等于正方形A,B的面积之和.
?同理,y?=3,z?=x?+y?=10,即最大正方形E的面积为10.
15.
【答案】100
?【解析】因为CE平分∠ACB,CF平分∠ACD,∠ACB+∠ACD=180°,所以∠ECF=90°,
?因为CE平分∠ACB,所以∠BCE=∠MCE,因为EF∥BC,所以∠CEM=∠BCE,
?所以∠CEM=∠MCE,所以ME=MC,
?同理可得∠MCF=∠MFC,所以EM=MC=MF=5,所以EF=10,
?在Rt△CEF中,由勾股定理可得CE2+CF2=EF2=100.
16.
【答案】=
?【解析】图中阴影部分的面积是以的三边AB、BC、CA为直径向外作的半圆,∴,,又∵在中,,三边满足勾股定理,则∴.
17.
【答案】4
?【解析】由图易证,最左端斜放置的正方形与相邻两个正方形所夹的两个直角三角形是两个全等的三角形,则易得.同理可证,∴.
18.(1)
【答案】因为∠BAC=90°,由勾股定理得.
?(2)
【答案】由三角形的面积得:,得,则AD=12.
?
19.
【答案】设BD=x,∵AD是底边BC上的高,AB=AC,∴,所以BC=2x,
?∵△ABC的周长为16,∴,∴AB=8-x,
?在Rt△ABD中,,即,解得x=3,
?∴AB=8-3=5,BC=2BD=2×3=6,
?∴△ABC的边AB,AC的长均为5,边BC的长为6.
?
20.
【答案】过点作,垂足为点.
?,,
?.
?空地的周长为.
?空地的面积为.
21.
【答案】如图,作出A点关于MN的对称点,连接交MN于点P,则的长就是最短路线的长,
?
?在中,由勾股定理求得.
?答:他要完成这件事情所走的最短路程是170?m.
?
22.(1)
【答案】平行;ED.
?(2)
【答案】∵,,
?∴与互余,与互余,∴,
?∵AC=BC,,
?∴,∴EC=AD,BE=CD,
?∴BE与AD之间的距离ED=EC-CD=AD-BE=6-2=4(cm).
?又∵,
?∴.
?
23.
【答案】过点B作于点D.设AD=x,则CD=21-x.
?
?在中,
?在中,
?∴,解得x=6,∴,∴BD=8.
?即AC边上的高为8.
?
24.
【答案】设DE=x,则EF=x,EC=8-x.在中,∵AD=AF=10,由勾股定理,得BF=6,∴FC=4.在中,由勾股定理,得,∴,∴x=5,即EC的长为3cm.
?
25.
【答案】由题意得AB=DE=2.5米,,
?在Rt△ABC中,根据勾股定理,得AC=2米.
?在Rt△CED中,根据勾股定理,得CE=1.5米,
?所以AE=2-1.5=0.5米,即AE的长为0.5米.
?
第10页
共10页
第9页
共10页
