2020-2021学年苏科版七年级数学下册第7章平面图形的认识(二) 练习题二(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册第7章平面图形的认识(二) 练习题二(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 132.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-02 10:35:32 | ||
图片预览


文档简介
七年级数学下册第7章平面图形的认识(二)
练习题二
1.直线EF、GH之间有一个Rt△ABC,其中∠BAC=90°,∠ABC=α.
(1)如图①,点A在直线EF上,点B、点C在直线GH上,若∠α=60°,∠FAC=30°.求证:EF∥GH;
(2)将三角形ABC如图②放置,点C、B分别在直线EF、GH上,直线EF∥GH,试探索∠FCA、∠A、∠ABH三者之间的数量关系;
(3)如图③,在图②的基础上,若BC平分∠ABH,CD平分∠FCA交直线GH于点D.试探索在α取不同数值时,∠BCD的大小是否发生变化?若不变求其值,若变化指出其变化范围.
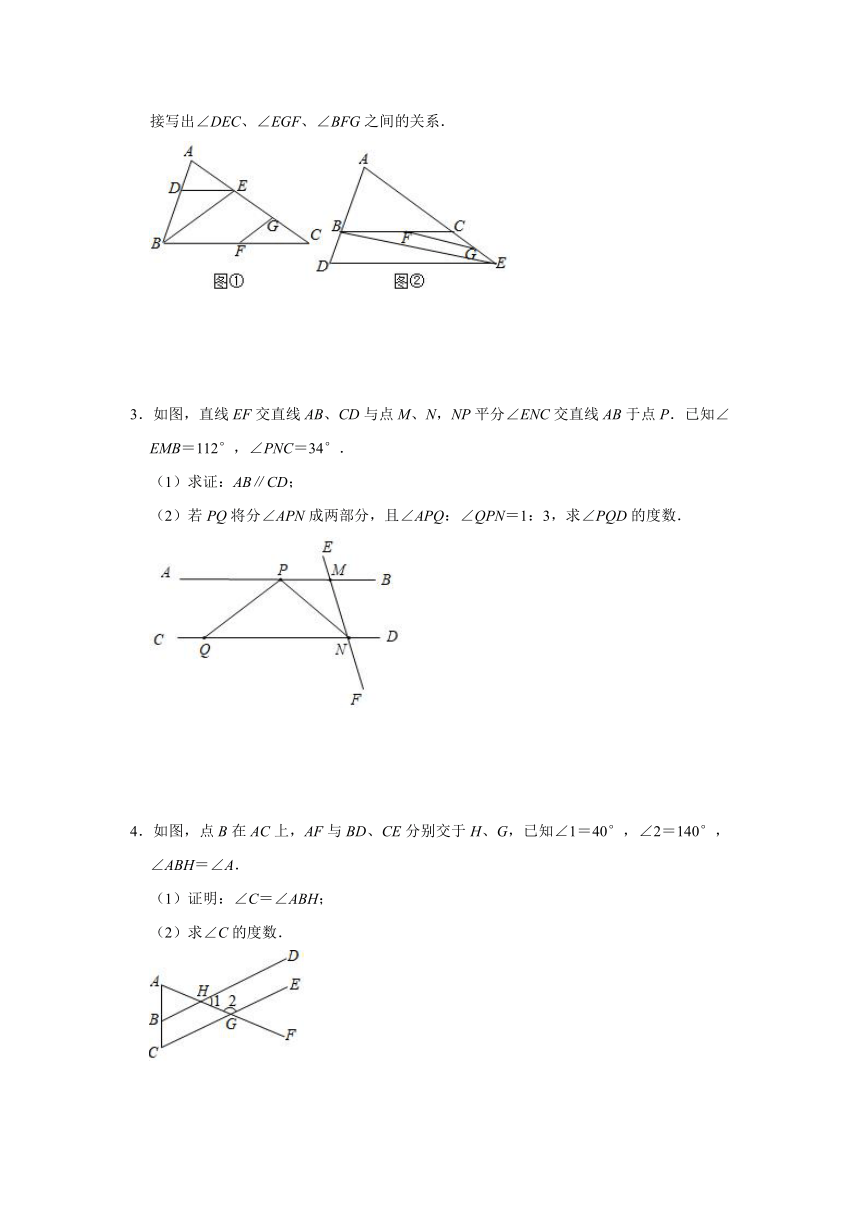
2.已知,△ABC,点E是直线AC上一个动点(不与A,C重合),点F是BC边上一个定点,过点E做DE∥BC,交直线AB于点D,连接BE,过点F作FG∥BE,交直线AC于点G.
(1)如图①,当点E在线段AC上时,求证:∠DEB=∠GFC;
(2)在(1)的条件下,判断∠DEC、∠EGF、∠BFG这三个角的度数和是否为一个定值?如果是,求出这个值,如果不是,说明理由;
(3)如图②,当点E在线段AC的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出∠DEC、∠EGF、∠BFG之间的关系;
(4)当点E在线段CA的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出∠DEC、∠EGF、∠BFG之间的关系.
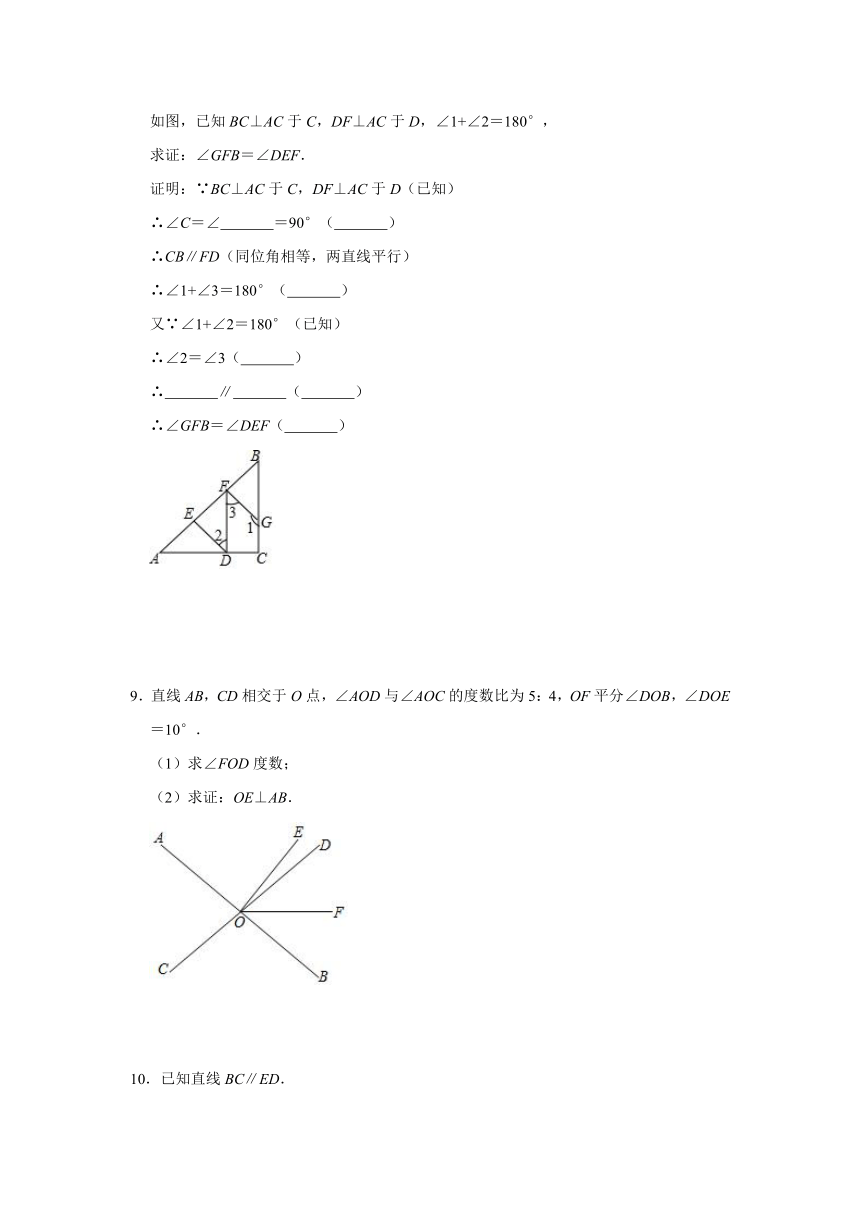
3.如图,直线EF交直线AB、CD与点M、N,NP平分∠ENC交直线AB于点P.已知∠EMB=112°,∠PNC=34°.
(1)求证:AB∥CD;
(2)若PQ将分∠APN成两部分,且∠APQ:∠QPN=1:3,求∠PQD的度数.
4.如图,点B在AC上,AF与BD、CE分别交于H、G,已知∠1=40°,∠2=140°,∠ABH=∠A.
(1)证明:∠C=∠ABH;
(2)求∠C的度数.
5.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:∠E+∠F=90°.
6.如图,OE⊥CD.OF⊥AB.
(1)已知过直线AB上O点有OC,OD,OE,OF4条射线,∠DOF=65°,求∠BOE,∠AOC的度数;
(2)若直线AB与直线CD相交于点O,∠DOF=2∠DOB,求图中各锐角的度数.
7.如图,直线AB、CD相交于点O,OE是∠AOD的平分线,OF⊥OE,若∠AOC=80°.求:
(1)∠BOE的度数;
(2)∠COF的度数.
8.阅读并填空完善下列证明过程:
如图,已知BC⊥AC于C,DF⊥AC于D,∠1+∠2=180°,
求证:∠GFB=∠DEF.
证明:∵BC⊥AC于C,DF⊥AC于D(已知)
∴∠C=∠
=90°(
)
∴CB∥FD(同位角相等,两直线平行)
∴∠1+∠3=180°(
)
又∵∠1+∠2=180°(已知)
∴∠2=∠3(
)
∴
∥
(
)
∴∠GFB=∠DEF(
)
9.直线AB,CD相交于O点,∠AOD与∠AOC的度数比为5:4,OF平分∠DOB,∠DOE=10°.
(1)求∠FOD度数;
(2)求证:OE⊥AB.
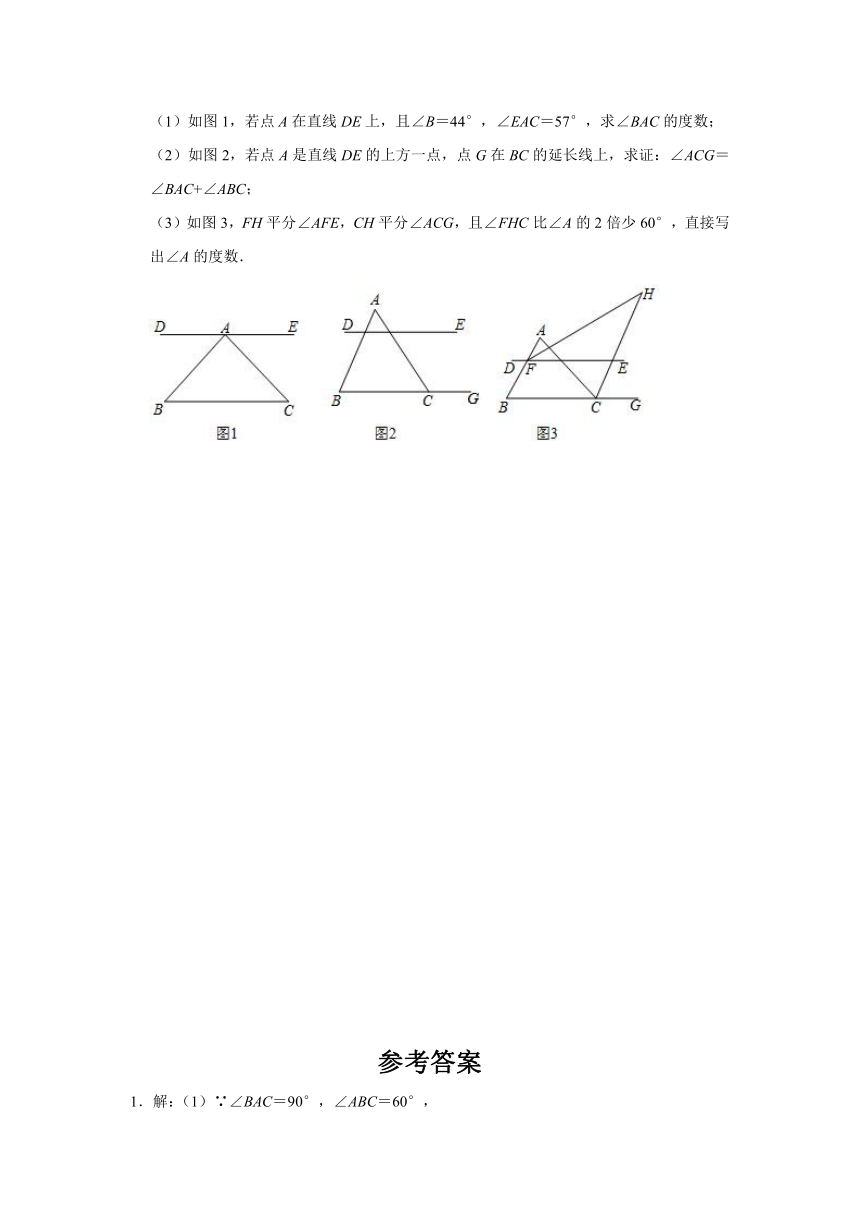
10.已知直线BC∥ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上,求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.
参考答案
1.解:(1)∵∠BAC=90°,∠ABC=60°,
∴∠ACB=30°,
∵∠FAC=30°,
∴∠FAC=∠ACB,
∴EF∥GH;
(2)如图2,过点A作AP∥EF,
则∠FCA+∠CAP=180°,
∴∠CAP=180°﹣∠FCA,
∵EF∥GH,
∴AP∥GH,
∴∠PAB+∠ABH=180°,
∴∠PAB=180°﹣∠ABH,
∴∠BAC=∠CAP+∠PAB
=180°﹣∠FCA+180°﹣∠ABH
=360°﹣∠FCA﹣∠ABH,
即∠BAC+∠FCA+∠ABH=360°;
(3)不发生变化,
理由是:如图3,过点A作AM∥GH,
又∵EF∥GH,
∴AM∥EF∥GH,
∴∠FCA+∠CAM=180°,∠MAB+∠ABH=180°,∠CBH=∠ECB,
又∵∠CAM+∠MAB=∠BAC=90°,
∴∠FCA+∠ABH=270°,
又∵BC平分∠ABH,CD平分∠FCA,
∴∠FCD+∠CBH=135°,
又∵∠CBH=∠ECB,即∠FCD+∠ECB=135°,
∴∠BCD=180°﹣(∠FCD+∠ECB)=45°.
2.解:(1)如图①所示:
∵DE∥BC,
∴∠DEB=∠EBC,
又∵FG∥BE,
∴∠EBC=∠GFC,
∴∠DEB=∠GFC;
(2)∠DEC+∠EGF+∠BFG=360°.
如图①所示,理由如下:
又∵FG∥BE,
∴∠EBC+∠BFG=180°,∠BEG+∠EGF=180°,
∴∠EBC+∠BFG+∠BEG+∠EGF=360°,
又∵DE∥BC,
∴∠DEB=∠EBG,
∴∠DEB+∠BFG+∠BEG+∠EGF=360°,
又∵∠DEC=∠DEB+∠BEG,
∴∠DEC+∠EGF+∠BFG=360°,
即三个角的和是一个定值;
(3)当点E在线段AC的延长线上时(2)结论仍然成立.
如图②所示,理由如下:
∵FG∥BE,
∴∠EGF+∠GEB=180°,
∠BFG+∠FBE=180°,
又∵BC∥DE,
∴∠BED=∠FBC,
∴∠DEC+∠EGF+∠BFG
=∠DEB+∠BEC+∠EGF+∠BFG
=∠FBE+∠BEC+∠EGF+∠BFG
=360°;
(4)点E在线段CA的延长线上时不成立.
如图③所示,理由如下:
∠EGF=180°﹣∠CGF,
∠BFG=180°﹣∠CFG,
∴∠EGF+∠BFG=360°﹣(∠CGF+∠CFG),
又∵∠C=180°﹣(∠CGF+∠CFG)
∴∠EGF+∠BFG=180°+∠C,
又∵DE∥BC,
∴∠DEC=∠C,
∴∠EGF+∠BFG=180°+∠DEC,
∴∠EGF+∠BFG﹣∠DEC=180°,
即点E在线段CA的延长线上时不成立.
3.(1)证明:∵∠EMB=112°,
∴∠PMN=112°,
∵NP平分∠EN,
∴∠CNE=2∠CNP,
∵∠CNP=34°,
∴∠CNE=68°,
∴∠PMN+∠CNE=180°,
∴AB∥CD;
(2)解:∵∠APN=∠PMN+∠PNM=112°+34°=146°,
∵∠APQ:∠QPN=1:3,
∴∠APQ=36.5°,
∵AB∥CD,
∴∠PQD=∠APQ,
∴∠PQD=36.5°.
4.(1)证明:∵∠1=40°,∠2=140°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠ABH=∠C;
(2)解:∵∠ABH=∠A,∠ABH=∠C,
∴∠A=∠C,
又∵∠A+∠C=∠2,∠2=140°,
∴∠C=2==70°.
5.解:(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=90°,
∴∠AOB=180°﹣90°=90°=∠EOF,
∴∠E+∠F=180°﹣∠EOF=90°.
6.解:(1)∵OE⊥CD.OF⊥AB,
∴∠DOE=90°,∠FOB=90°,
∵∠DOF=65°,
∴∠BOD=∠FOB﹣DOF=90°﹣65°=25°,
∴∠BOE=∠DOE﹣∠BOD=90°﹣25°=65°,
∠AOC=∠BOD=25°.
答:∠BOE,∠AOC的度数为65°,25°;
(2)∵∠DOF=2∠DOB,∠FOB=90°,
∴∠DOF+∠DOB=90°,
∴3∠DOB=90°,
∴∠DOB=30°,
∴∠DOF=∠BOE=60°,
∴∠AOC=∠BOD=30°.
答:图中各锐角的度数为∠DOF=∠BOE=60°,∠AOC=∠BOD=30°.
7.解(1)∵直线AB、CD相交于点O,
∴∠AOC+∠AOD=180°,∠BOE+∠AOE=180°,
∵∠AOC=80°,
∴∠AOD=180°﹣80°=100°,
∵OE平分∠AOD,
∴∠AOE=∠AOD=50°.
∴∠BOE=180°﹣∠AOE=180°﹣50°=130°;
(2)由(1)得∠AOE=50°.
∵OF⊥OE,
∴∠EOF=90°,
即∠AOE+∠AOF=90°.
∴∠AOF=90°﹣∠AOE=90°﹣50°=40°.
∵∠AOC=80°,
∴∠COF=80°﹣∠AOF=80°﹣40°=40°.
8.证明:∵BC⊥AC于C,DF⊥AC于D(已知)
∴∠C=∠ADF=90°(垂直的定义)
∴CB∥FD
(同位角相等,两直线平行
)
∴∠1+∠3=180°(两直线平行,同旁内角互补)
又∵∠1+∠2=180°(已知)
∴∠2=∠3(同角的补角相等)
∴DE∥FG
(内错角相等,两直线平行)
∴∠GFB=∠DEF
(两直线平行,同位角相等),
故答案为:ADF;垂直的定义;两直线平行,同旁内角互补;同角的补角相等;DE;FG;内错角相等,两直线平行;两直线平行,同位角相等.
9.解:(1)∵∠AOD与∠AOC的度数比为5:4,
设∠AOD=5x,∠AOC=4x,
∴∠BOD=∠AOC=4x,
∵∠AOD+∠BOD=180°,
即5x+4x=180°,
解得:x=20°,
∴∠DOB=80°,
∵OF平分∠DOB,
∴∠DOF=40°;
(2)∵OF平分∠DOB,
∴∠DOF=∠BOF=40°,
∴∠EOB=∠EOD+∠DOB=10°+80°=90°,
∴OE⊥AB.
10.解:(1)∵BC∥ED,∠B=44°,
∴∠DAB=∠B=44°,
∵∠BAC=180°﹣∠DAB﹣∠EAC
∴∠BAC=180°﹣44°﹣57°=79°.
(2)过点A作MN∥BG,
∴∠ACG=∠MAC,∠ABC=∠MAB
而∠MAC=∠MAB+∠BAC
∴∠ACG=∠MAB+∠BAC=∠ABC+∠BAC.
(3)如图,设AC与FH交于点P
∵FH平分∠AFE,CH平分∠ACG
∴∠AFH=∠EFH=∠AFE,∠ACH=∠HCG=∠ACG
∵BC∥ED
∴∠AFE=∠B
∴∠AFH=∠B
∵∠A+∠B=∠ACG
∴∠ACH=∠ACG=∠A+∠B
在△APF和△CPH中
∵∠APF=∠CPH
∴∠A+∠B=∠A+∠B+∠FHC
∴∠FHC=∠A
∵∠FCH=2∠A﹣60°
∴∠A=2∠A﹣60°
∴∠A=40°.
练习题二
1.直线EF、GH之间有一个Rt△ABC,其中∠BAC=90°,∠ABC=α.
(1)如图①,点A在直线EF上,点B、点C在直线GH上,若∠α=60°,∠FAC=30°.求证:EF∥GH;
(2)将三角形ABC如图②放置,点C、B分别在直线EF、GH上,直线EF∥GH,试探索∠FCA、∠A、∠ABH三者之间的数量关系;
(3)如图③,在图②的基础上,若BC平分∠ABH,CD平分∠FCA交直线GH于点D.试探索在α取不同数值时,∠BCD的大小是否发生变化?若不变求其值,若变化指出其变化范围.
2.已知,△ABC,点E是直线AC上一个动点(不与A,C重合),点F是BC边上一个定点,过点E做DE∥BC,交直线AB于点D,连接BE,过点F作FG∥BE,交直线AC于点G.
(1)如图①,当点E在线段AC上时,求证:∠DEB=∠GFC;
(2)在(1)的条件下,判断∠DEC、∠EGF、∠BFG这三个角的度数和是否为一个定值?如果是,求出这个值,如果不是,说明理由;
(3)如图②,当点E在线段AC的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出∠DEC、∠EGF、∠BFG之间的关系;
(4)当点E在线段CA的延长线上时,(2)中的结论是否仍然成立?如果不成立,请直接写出∠DEC、∠EGF、∠BFG之间的关系.
3.如图,直线EF交直线AB、CD与点M、N,NP平分∠ENC交直线AB于点P.已知∠EMB=112°,∠PNC=34°.
(1)求证:AB∥CD;
(2)若PQ将分∠APN成两部分,且∠APQ:∠QPN=1:3,求∠PQD的度数.
4.如图,点B在AC上,AF与BD、CE分别交于H、G,已知∠1=40°,∠2=140°,∠ABH=∠A.
(1)证明:∠C=∠ABH;
(2)求∠C的度数.
5.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:∠E+∠F=90°.
6.如图,OE⊥CD.OF⊥AB.
(1)已知过直线AB上O点有OC,OD,OE,OF4条射线,∠DOF=65°,求∠BOE,∠AOC的度数;
(2)若直线AB与直线CD相交于点O,∠DOF=2∠DOB,求图中各锐角的度数.
7.如图,直线AB、CD相交于点O,OE是∠AOD的平分线,OF⊥OE,若∠AOC=80°.求:
(1)∠BOE的度数;
(2)∠COF的度数.
8.阅读并填空完善下列证明过程:
如图,已知BC⊥AC于C,DF⊥AC于D,∠1+∠2=180°,
求证:∠GFB=∠DEF.
证明:∵BC⊥AC于C,DF⊥AC于D(已知)
∴∠C=∠
=90°(
)
∴CB∥FD(同位角相等,两直线平行)
∴∠1+∠3=180°(
)
又∵∠1+∠2=180°(已知)
∴∠2=∠3(
)
∴
∥
(
)
∴∠GFB=∠DEF(
)
9.直线AB,CD相交于O点,∠AOD与∠AOC的度数比为5:4,OF平分∠DOB,∠DOE=10°.
(1)求∠FOD度数;
(2)求证:OE⊥AB.
10.已知直线BC∥ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上,求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.
参考答案
1.解:(1)∵∠BAC=90°,∠ABC=60°,
∴∠ACB=30°,
∵∠FAC=30°,
∴∠FAC=∠ACB,
∴EF∥GH;
(2)如图2,过点A作AP∥EF,
则∠FCA+∠CAP=180°,
∴∠CAP=180°﹣∠FCA,
∵EF∥GH,
∴AP∥GH,
∴∠PAB+∠ABH=180°,
∴∠PAB=180°﹣∠ABH,
∴∠BAC=∠CAP+∠PAB
=180°﹣∠FCA+180°﹣∠ABH
=360°﹣∠FCA﹣∠ABH,
即∠BAC+∠FCA+∠ABH=360°;
(3)不发生变化,
理由是:如图3,过点A作AM∥GH,
又∵EF∥GH,
∴AM∥EF∥GH,
∴∠FCA+∠CAM=180°,∠MAB+∠ABH=180°,∠CBH=∠ECB,
又∵∠CAM+∠MAB=∠BAC=90°,
∴∠FCA+∠ABH=270°,
又∵BC平分∠ABH,CD平分∠FCA,
∴∠FCD+∠CBH=135°,
又∵∠CBH=∠ECB,即∠FCD+∠ECB=135°,
∴∠BCD=180°﹣(∠FCD+∠ECB)=45°.
2.解:(1)如图①所示:
∵DE∥BC,
∴∠DEB=∠EBC,
又∵FG∥BE,
∴∠EBC=∠GFC,
∴∠DEB=∠GFC;
(2)∠DEC+∠EGF+∠BFG=360°.
如图①所示,理由如下:
又∵FG∥BE,
∴∠EBC+∠BFG=180°,∠BEG+∠EGF=180°,
∴∠EBC+∠BFG+∠BEG+∠EGF=360°,
又∵DE∥BC,
∴∠DEB=∠EBG,
∴∠DEB+∠BFG+∠BEG+∠EGF=360°,
又∵∠DEC=∠DEB+∠BEG,
∴∠DEC+∠EGF+∠BFG=360°,
即三个角的和是一个定值;
(3)当点E在线段AC的延长线上时(2)结论仍然成立.
如图②所示,理由如下:
∵FG∥BE,
∴∠EGF+∠GEB=180°,
∠BFG+∠FBE=180°,
又∵BC∥DE,
∴∠BED=∠FBC,
∴∠DEC+∠EGF+∠BFG
=∠DEB+∠BEC+∠EGF+∠BFG
=∠FBE+∠BEC+∠EGF+∠BFG
=360°;
(4)点E在线段CA的延长线上时不成立.
如图③所示,理由如下:
∠EGF=180°﹣∠CGF,
∠BFG=180°﹣∠CFG,
∴∠EGF+∠BFG=360°﹣(∠CGF+∠CFG),
又∵∠C=180°﹣(∠CGF+∠CFG)
∴∠EGF+∠BFG=180°+∠C,
又∵DE∥BC,
∴∠DEC=∠C,
∴∠EGF+∠BFG=180°+∠DEC,
∴∠EGF+∠BFG﹣∠DEC=180°,
即点E在线段CA的延长线上时不成立.
3.(1)证明:∵∠EMB=112°,
∴∠PMN=112°,
∵NP平分∠EN,
∴∠CNE=2∠CNP,
∵∠CNP=34°,
∴∠CNE=68°,
∴∠PMN+∠CNE=180°,
∴AB∥CD;
(2)解:∵∠APN=∠PMN+∠PNM=112°+34°=146°,
∵∠APQ:∠QPN=1:3,
∴∠APQ=36.5°,
∵AB∥CD,
∴∠PQD=∠APQ,
∴∠PQD=36.5°.
4.(1)证明:∵∠1=40°,∠2=140°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠ABH=∠C;
(2)解:∵∠ABH=∠A,∠ABH=∠C,
∴∠A=∠C,
又∵∠A+∠C=∠2,∠2=140°,
∴∠C=2==70°.
5.解:(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=90°,
∴∠AOB=180°﹣90°=90°=∠EOF,
∴∠E+∠F=180°﹣∠EOF=90°.
6.解:(1)∵OE⊥CD.OF⊥AB,
∴∠DOE=90°,∠FOB=90°,
∵∠DOF=65°,
∴∠BOD=∠FOB﹣DOF=90°﹣65°=25°,
∴∠BOE=∠DOE﹣∠BOD=90°﹣25°=65°,
∠AOC=∠BOD=25°.
答:∠BOE,∠AOC的度数为65°,25°;
(2)∵∠DOF=2∠DOB,∠FOB=90°,
∴∠DOF+∠DOB=90°,
∴3∠DOB=90°,
∴∠DOB=30°,
∴∠DOF=∠BOE=60°,
∴∠AOC=∠BOD=30°.
答:图中各锐角的度数为∠DOF=∠BOE=60°,∠AOC=∠BOD=30°.
7.解(1)∵直线AB、CD相交于点O,
∴∠AOC+∠AOD=180°,∠BOE+∠AOE=180°,
∵∠AOC=80°,
∴∠AOD=180°﹣80°=100°,
∵OE平分∠AOD,
∴∠AOE=∠AOD=50°.
∴∠BOE=180°﹣∠AOE=180°﹣50°=130°;
(2)由(1)得∠AOE=50°.
∵OF⊥OE,
∴∠EOF=90°,
即∠AOE+∠AOF=90°.
∴∠AOF=90°﹣∠AOE=90°﹣50°=40°.
∵∠AOC=80°,
∴∠COF=80°﹣∠AOF=80°﹣40°=40°.
8.证明:∵BC⊥AC于C,DF⊥AC于D(已知)
∴∠C=∠ADF=90°(垂直的定义)
∴CB∥FD
(同位角相等,两直线平行
)
∴∠1+∠3=180°(两直线平行,同旁内角互补)
又∵∠1+∠2=180°(已知)
∴∠2=∠3(同角的补角相等)
∴DE∥FG
(内错角相等,两直线平行)
∴∠GFB=∠DEF
(两直线平行,同位角相等),
故答案为:ADF;垂直的定义;两直线平行,同旁内角互补;同角的补角相等;DE;FG;内错角相等,两直线平行;两直线平行,同位角相等.
9.解:(1)∵∠AOD与∠AOC的度数比为5:4,
设∠AOD=5x,∠AOC=4x,
∴∠BOD=∠AOC=4x,
∵∠AOD+∠BOD=180°,
即5x+4x=180°,
解得:x=20°,
∴∠DOB=80°,
∵OF平分∠DOB,
∴∠DOF=40°;
(2)∵OF平分∠DOB,
∴∠DOF=∠BOF=40°,
∴∠EOB=∠EOD+∠DOB=10°+80°=90°,
∴OE⊥AB.
10.解:(1)∵BC∥ED,∠B=44°,
∴∠DAB=∠B=44°,
∵∠BAC=180°﹣∠DAB﹣∠EAC
∴∠BAC=180°﹣44°﹣57°=79°.
(2)过点A作MN∥BG,
∴∠ACG=∠MAC,∠ABC=∠MAB
而∠MAC=∠MAB+∠BAC
∴∠ACG=∠MAB+∠BAC=∠ABC+∠BAC.
(3)如图,设AC与FH交于点P
∵FH平分∠AFE,CH平分∠ACG
∴∠AFH=∠EFH=∠AFE,∠ACH=∠HCG=∠ACG
∵BC∥ED
∴∠AFE=∠B
∴∠AFH=∠B
∵∠A+∠B=∠ACG
∴∠ACH=∠ACG=∠A+∠B
在△APF和△CPH中
∵∠APF=∠CPH
∴∠A+∠B=∠A+∠B+∠FHC
∴∠FHC=∠A
∵∠FCH=2∠A﹣60°
∴∠A=2∠A﹣60°
∴∠A=40°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
