2020-2021学年苏科版七年级数学下册第7章平面图形的认识(二) 练习题三(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册第7章平面图形的认识(二) 练习题三(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 125.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-02 00:00:00 | ||
图片预览

文档简介
七年级数学下册第7章平面图形的认识(二)
练习题三
1.完成推理填空
如图,已知∠B=∠D,∠BAE=∠E.将证明∠AFC+∠DAE=180°的过程填写完整.
证明:∵∠BAE=∠E,
∴
∥
(
).
∴∠B=∠
(
).
又∵∠B=∠D,
∴∠D=∠
(等量代换).
∴AD∥BC(
).
∴∠AFC+∠DAE=180°(
).
2.如图,∠A=90°,BD平分∠ABC,交AC于点D,DE⊥BC于点E,DF∥AB交BC于点F.
(1)依题意补全图形;
(2)设∠C=α,
①∠ABD=
(用含α的式子表示);
②猜想∠BDF与∠DFC的数量关系,并证明.
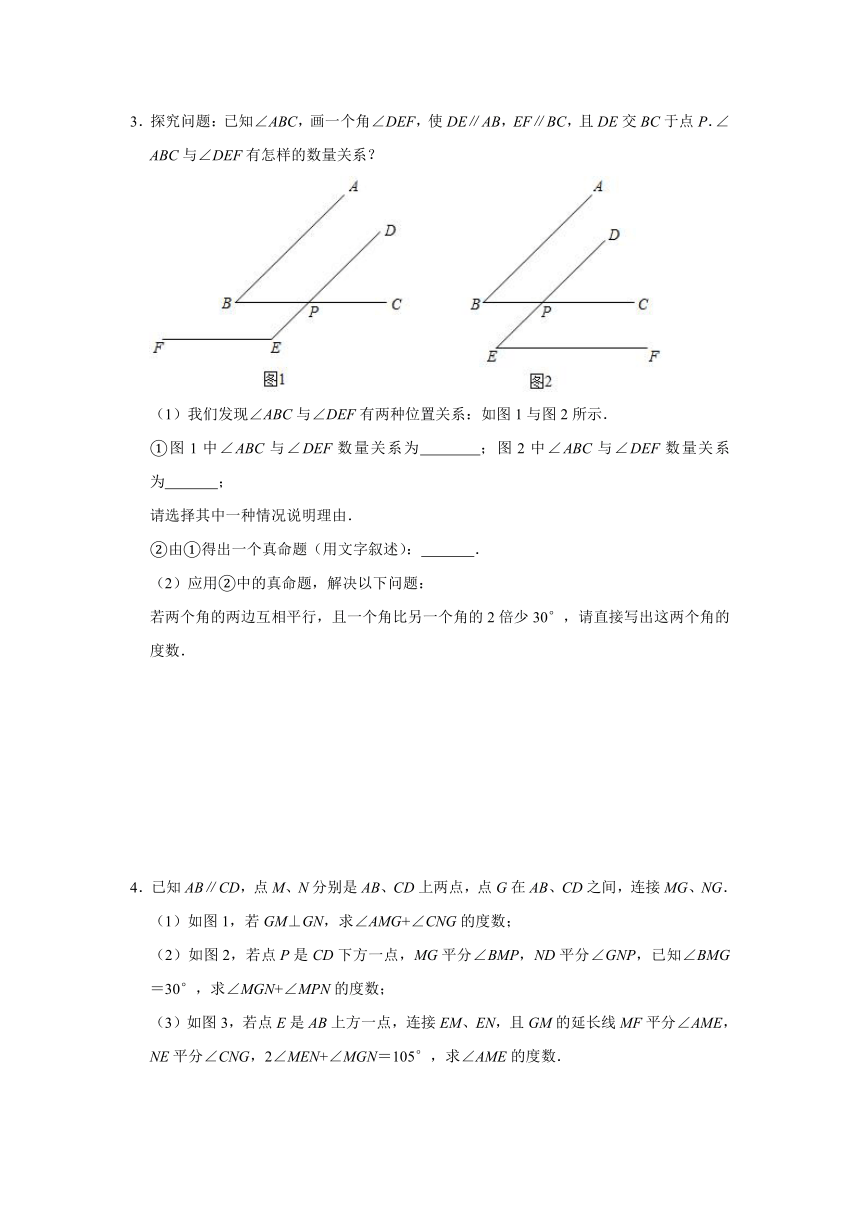
3.探究问题:已知∠ABC,画一个角∠DEF,使DE∥AB,EF∥BC,且DE交BC于点P.∠ABC与∠DEF有怎样的数量关系?
(1)我们发现∠ABC与∠DEF有两种位置关系:如图1与图2所示.
①图1中∠ABC与∠DEF数量关系为
;图2中∠ABC与∠DEF数量关系为
;
请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述):
.
(2)应用②中的真命题,解决以下问题:
若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
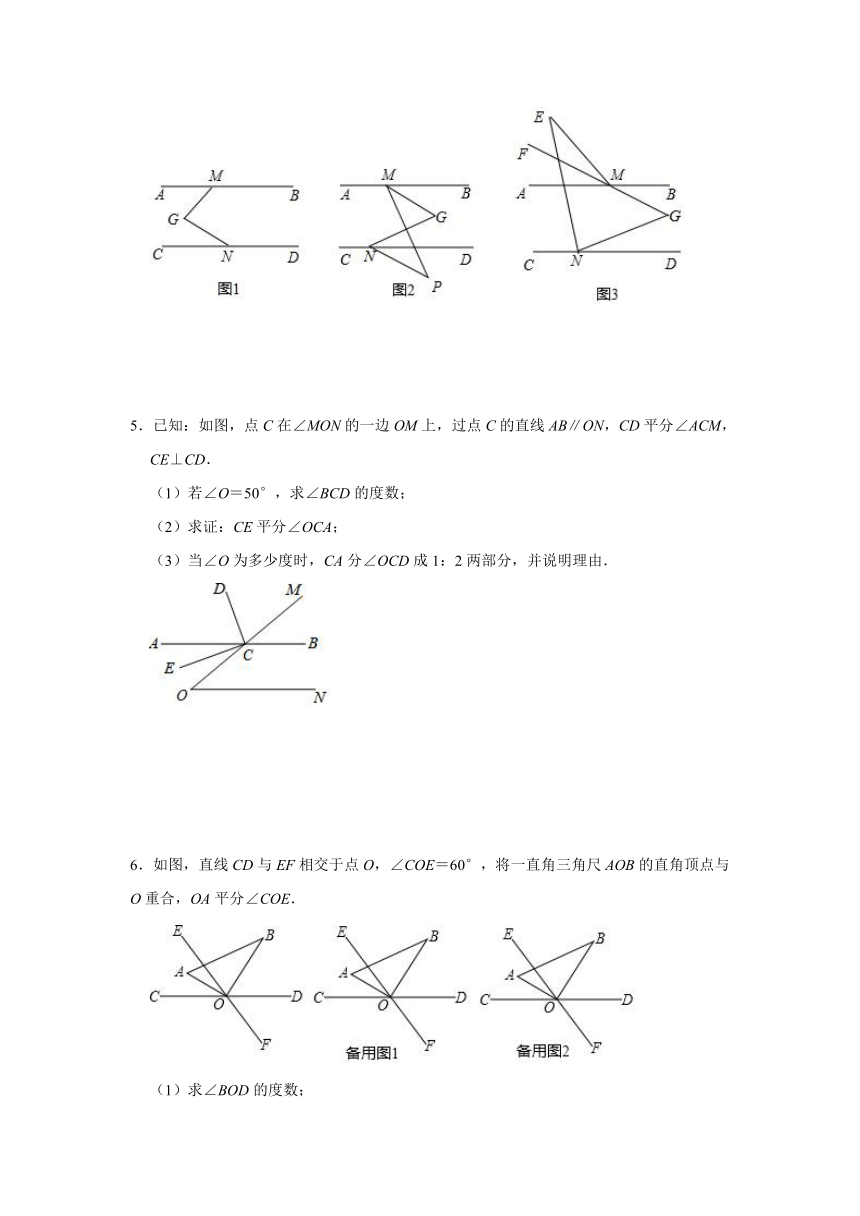
4.已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.
(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=30°,求∠MGN+∠MPN的度数;
(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.
5.已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
6.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
(1)求∠BOD的度数;
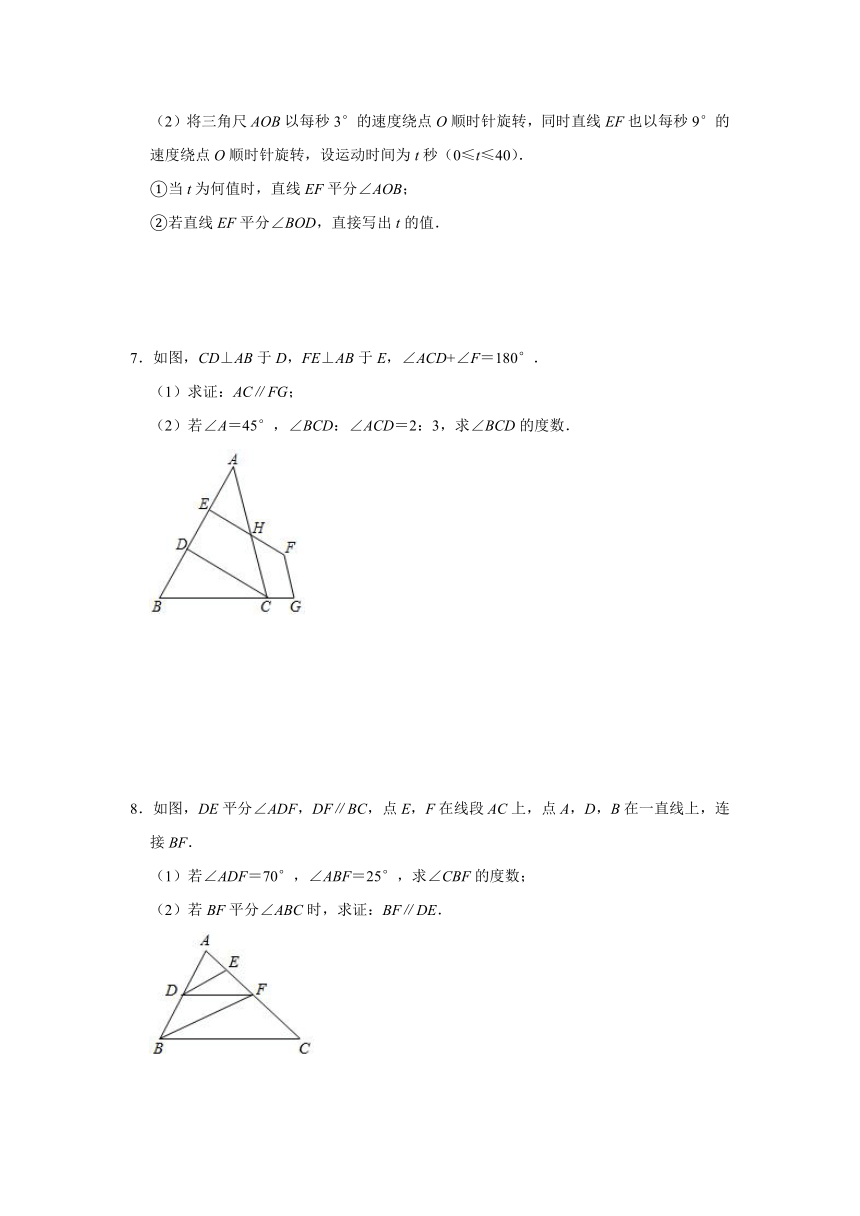
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
7.如图,CD⊥AB于D,FE⊥AB于E,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
8.如图,DE平分∠ADF,DF∥BC,点E,F在线段AC上,点A,D,B在一直线上,连接BF.
(1)若∠ADF=70°,∠ABF=25°,求∠CBF的度数;
(2)若BF平分∠ABC时,求证:BF∥DE.
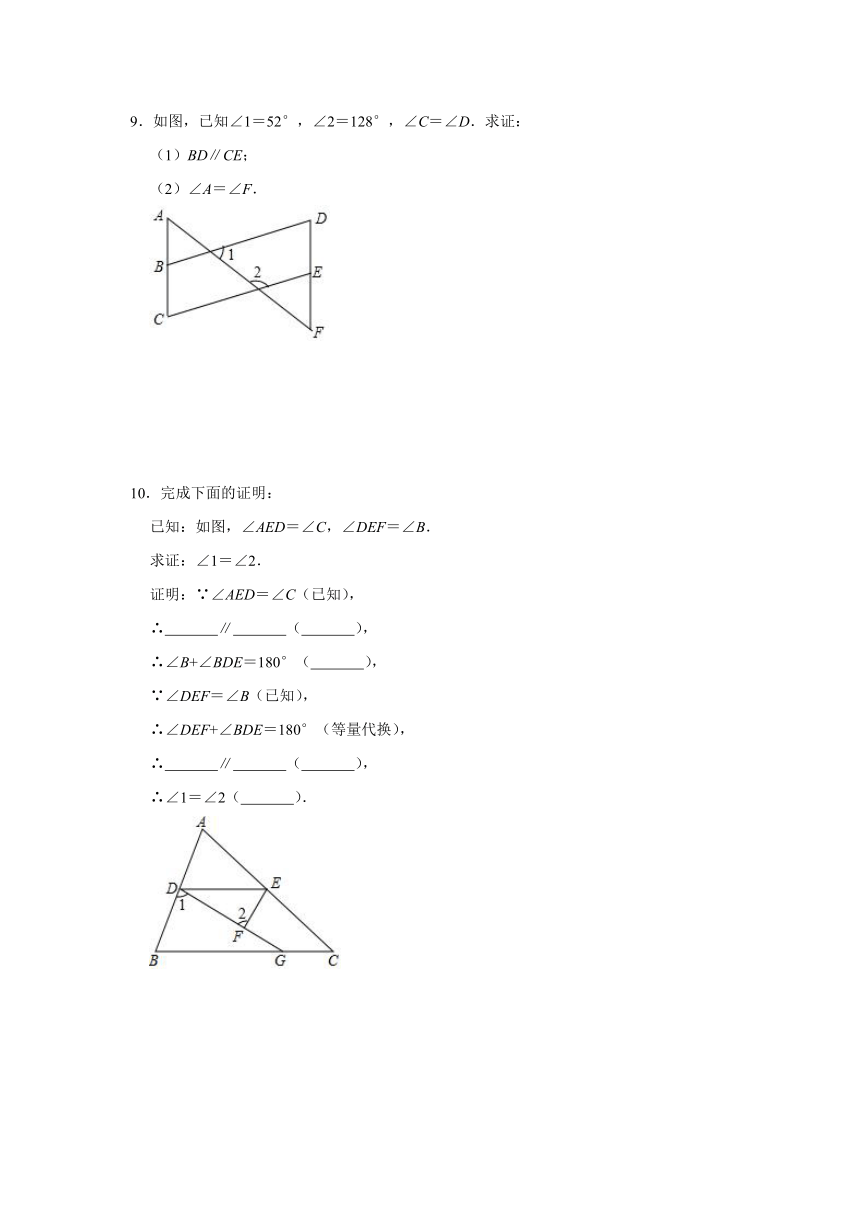
9.如图,已知∠1=52°,∠2=128°,∠C=∠D.求证:
(1)BD∥CE;
(2)∠A=∠F.
10.完成下面的证明:
已知:如图,∠AED=∠C,∠DEF=∠B.
求证:∠1=∠2.
证明:∵∠AED=∠C(已知),
∴
∥
(
),
∴∠B+∠BDE=180°(
),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴
∥
(
),
∴∠1=∠2(
).
参考答案
1.证明:∵∠BAE=∠E,
∴AB∥DE(内错角相等,两直线平行).
∴∠B=∠BCE(两直线平行,内错角相等).
又∵∠B=∠D,
∴∠D=∠BCE(等量代换).
∴AD∥BC(同位角相等,两直线平行).
∴∠AFC+∠DAE=180°(两直线平行,同旁内角互补).
故答案为:AB,DE,内错角相等,两直线平行;BCE,两直线平行,内错角相等;BCE,同位角相等,两直线平行;两直线平行,同旁内角互补.
2.(1)如图:
(2)①∵∠A=90°,
∴∠ABC=90°﹣∠C=90°﹣α,
∵BD平分∠ABC,
∴∠ABD==(90°﹣α)=45°﹣α,
故答案为45°﹣α;
②∠DFC=2∠BDF,
证明:∵DF∥AB,
∴∠DFC=∠ABC.
∠ABD=∠BDF.
∵BD平分∠ABC,
∴∠ABC=2∠ABD.
∴∠DFC=2∠BDF.
3.解:(1)①如图1中,∠ABC+∠DEF=180°.如图2中,∠ABC=∠DEF,
故答案为:∠ABC+∠DEF=180°,∠ABC=∠DEF.
理由:如图1中,
∵BC∥EF,
∴∠DPB=∠DEF,
∵AB∥DE,
∴∠ABC+∠DPB=180°,
∴∠ABC+∠DEF=180°.
如图2中,∵BC∥EF,
∴∠DPC=∠DEF,
∵AB∥DE,
∴∠ABC=∠DPC,
∴∠ABC=∠DEF.
②结论:如果两个角的两边互相平行,那么这两个角相等或互补.
故答案为:如果两个角的两边互相平行,那么这两个角相等或互补.
(2)设两个角分别为x和2x﹣30°,
由题意x=2x﹣30°或x+2x﹣30°=180°,
解得x=30°或x=70°,
∴这两个角的度数为30°,30°或70°和110°.
4.解:(1)如图1,过G作GH∥AB,
∵AB∥CD,
∴GH∥AB∥CD,
∴∠AMG=∠HGM,∠CNG=∠HGN,
∵MG⊥NG,
∴∠MGN=∠MGH+∠NGH=∠AMG+∠CNG=90°;
(2)如图2,过G作GK∥AB,过点P作PQ∥AB,设∠GND=α,
∵GK∥AB,AB∥CD,
∴GK∥CD,
∴∠KGN=∠GND=α,
∵GK∥AB,∠BMG=30°,
∴∠MGK=∠BMG=30°,
∵MG平分∠BMP,ND平分∠GNP,
∴∠GMP=∠BMG=30°,
∴∠BMP=60°,
∵PQ∥AB,
∴∠MPQ=∠BMP=60°,
∵ND平分∠GNP,
∴∠DNP=∠GND=α,
∵AB∥CD,
∴PQ∥CD,
∴∠QPN=∠DNP=α,
∴∠MGN=30°+α,∠MPN=60°﹣α,
∴∠MGN+∠MPN=30°+α+60°﹣α=90°;
(3)如图3,过G作GK∥AB,过E作ET∥AB,设∠AMF=x,∠GND=y,
∵AB,FG交于M,MF平分∠AME,
∴∠FME=∠FMA=∠BMG=x,
∴∠AME=2x,
∵GK∥AB,
∴∠MGK=∠BMG=x,
∵ET∥AB,
∴∠TEM=∠EMA=2x,
∵CD∥AB∥KG,
∴GK∥CD,
∴∠KGN=∠GND=y,
∴∠MGN=x+y,
∵∠CND=180°,NE平分∠CNG,
∴∠CNG=180°﹣y,∠CNE=∠CNG=90°﹣y,
∵ET∥AB∥CD,
∴ET∥CD,
∴∠TEN=∠CNE=90°﹣y,
∴∠MEN=∠TEN﹣∠TEM=90°﹣y﹣2x,∠MGN=x+y,
∵2∠MEN+∠G=105°,
∴2(90°﹣y﹣2x)+x+y=105°,
∴x=25°,
∴∠AME=2x=50°.
5.解:(1)∵AB∥ON
∴∠O=∠MCB(两直线平行,同位角相等)
∵∠O=50°
∴∠MCB=50°
∵∠ACM+∠MCB=180°(平角定义)
∴∠ACM=180°﹣50°=130°
又∵CD平分∠ACM
∴∠DCM=65°(角平分线定义)
∴∠BCD=∠DCM+∠MCB=65°+50°=115°
(2)证明:∵CE⊥CD
∴∠DCE=90°
∴∠ACE+∠DCA=90°
又∵∠MCO=180°(平角定义)
∴∠ECO+∠DCM=90°
∵∠DCA=∠DCM
∴∠ACE=∠ECO(等角的余角相等)
即CE平分∠OCA
(3)结论:当∠O=36°或90°时,CA分∠OCD成1:2两部分
①当∠O=36°时
∵AB∥ON
∴∠ACO=∠O=36°
∴∠ACM=144°
又∵CD平分∠ACM
∴∠ACD=72°
∴∠ACO=∠ACD
即CA分∠OCD成1:2两部分
②当∠O=90°时
∵AB∥ON
∴∠ACO=∠O=90°
∴∠ACM=90°
又∵CD平分∠ACM
∴∠ACD=45°
∴∠ACD=∠ACO
即CA分∠OCD成1:2两部分
6.解:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
①当OE平分∠AOB时,∠AOE=45°,
即9°t+30°﹣3°t=45°,
解得t=2.5;
②当OF平分∠AOB时,∠AOF=45°,
即9°t﹣150°﹣3°t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
①当OE平分∠BOD时,∠BOE=∠BOD,
即9°t﹣60°﹣3°t=(60°﹣3°t),
解得t=12;
②当OF平分∠BOD时,∠DOF=∠BOD,
即9°t﹣300°=(3°t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.
7.(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AFH=∠ADC=90°,
∴EF∥DC,
∴∠AHE=∠ACD,
∵∠ACD+∠F=180°.
∴∠AHE+∠F=180°,
∵∠AHE+∠EHC=180°,
∴∠EHC=∠F,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
∴设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴解得x=15°,
∴∠BCD=2x=30°.
答:∠BCD的度数为30°.
8.解:(1)∵DF∥BC,
∴∠ABC=∠ADF=70°,
∵∠ABF=25°,
∴∠CBF=70°﹣25°=45°;
(2)证明:∵DF∥BC,
∴∠ABC=∠ADF,
∵BF平分∠ABC,DE平分∠ADF,
∴∠ADE=ADF,∠ABF=ABC,
∴∠ADE=∠ABF,
∴BF∥DE.
9.证明:(1)∵∠1=52°,∠2=128°,
∴∠1+∠2=180°,
∴BD∥CE;
(2)∵BD∥CE,
∴∠C=∠ABD,
又∵∠C=∠D,
∴∠ABD=∠D,
∵AC∥DF,
∴∠A=∠F.
10.解:∵∠AED=∠C(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠B+∠BDE=180°
(两直线平行,同旁内角互补),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°
(等量代换),
∴EF∥AB(同旁内角互补,两直线平行),
∴∠1=∠2
(两直线平行,内错角相等).
故答案为:DE;BC;同位角相等,两直线平行;两直线平行,同旁内角互补;EF;AB;同旁内角互补,两直线平行;两直线平行,内错角相等.
练习题三
1.完成推理填空
如图,已知∠B=∠D,∠BAE=∠E.将证明∠AFC+∠DAE=180°的过程填写完整.
证明:∵∠BAE=∠E,
∴
∥
(
).
∴∠B=∠
(
).
又∵∠B=∠D,
∴∠D=∠
(等量代换).
∴AD∥BC(
).
∴∠AFC+∠DAE=180°(
).
2.如图,∠A=90°,BD平分∠ABC,交AC于点D,DE⊥BC于点E,DF∥AB交BC于点F.
(1)依题意补全图形;
(2)设∠C=α,
①∠ABD=
(用含α的式子表示);
②猜想∠BDF与∠DFC的数量关系,并证明.
3.探究问题:已知∠ABC,画一个角∠DEF,使DE∥AB,EF∥BC,且DE交BC于点P.∠ABC与∠DEF有怎样的数量关系?
(1)我们发现∠ABC与∠DEF有两种位置关系:如图1与图2所示.
①图1中∠ABC与∠DEF数量关系为
;图2中∠ABC与∠DEF数量关系为
;
请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述):
.
(2)应用②中的真命题,解决以下问题:
若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
4.已知AB∥CD,点M、N分别是AB、CD上两点,点G在AB、CD之间,连接MG、NG.
(1)如图1,若GM⊥GN,求∠AMG+∠CNG的度数;
(2)如图2,若点P是CD下方一点,MG平分∠BMP,ND平分∠GNP,已知∠BMG=30°,求∠MGN+∠MPN的度数;
(3)如图3,若点E是AB上方一点,连接EM、EN,且GM的延长线MF平分∠AME,NE平分∠CNG,2∠MEN+∠MGN=105°,求∠AME的度数.
5.已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.
6.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
7.如图,CD⊥AB于D,FE⊥AB于E,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
8.如图,DE平分∠ADF,DF∥BC,点E,F在线段AC上,点A,D,B在一直线上,连接BF.
(1)若∠ADF=70°,∠ABF=25°,求∠CBF的度数;
(2)若BF平分∠ABC时,求证:BF∥DE.
9.如图,已知∠1=52°,∠2=128°,∠C=∠D.求证:
(1)BD∥CE;
(2)∠A=∠F.
10.完成下面的证明:
已知:如图,∠AED=∠C,∠DEF=∠B.
求证:∠1=∠2.
证明:∵∠AED=∠C(已知),
∴
∥
(
),
∴∠B+∠BDE=180°(
),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°(等量代换),
∴
∥
(
),
∴∠1=∠2(
).
参考答案
1.证明:∵∠BAE=∠E,
∴AB∥DE(内错角相等,两直线平行).
∴∠B=∠BCE(两直线平行,内错角相等).
又∵∠B=∠D,
∴∠D=∠BCE(等量代换).
∴AD∥BC(同位角相等,两直线平行).
∴∠AFC+∠DAE=180°(两直线平行,同旁内角互补).
故答案为:AB,DE,内错角相等,两直线平行;BCE,两直线平行,内错角相等;BCE,同位角相等,两直线平行;两直线平行,同旁内角互补.
2.(1)如图:
(2)①∵∠A=90°,
∴∠ABC=90°﹣∠C=90°﹣α,
∵BD平分∠ABC,
∴∠ABD==(90°﹣α)=45°﹣α,
故答案为45°﹣α;
②∠DFC=2∠BDF,
证明:∵DF∥AB,
∴∠DFC=∠ABC.
∠ABD=∠BDF.
∵BD平分∠ABC,
∴∠ABC=2∠ABD.
∴∠DFC=2∠BDF.
3.解:(1)①如图1中,∠ABC+∠DEF=180°.如图2中,∠ABC=∠DEF,
故答案为:∠ABC+∠DEF=180°,∠ABC=∠DEF.
理由:如图1中,
∵BC∥EF,
∴∠DPB=∠DEF,
∵AB∥DE,
∴∠ABC+∠DPB=180°,
∴∠ABC+∠DEF=180°.
如图2中,∵BC∥EF,
∴∠DPC=∠DEF,
∵AB∥DE,
∴∠ABC=∠DPC,
∴∠ABC=∠DEF.
②结论:如果两个角的两边互相平行,那么这两个角相等或互补.
故答案为:如果两个角的两边互相平行,那么这两个角相等或互补.
(2)设两个角分别为x和2x﹣30°,
由题意x=2x﹣30°或x+2x﹣30°=180°,
解得x=30°或x=70°,
∴这两个角的度数为30°,30°或70°和110°.
4.解:(1)如图1,过G作GH∥AB,
∵AB∥CD,
∴GH∥AB∥CD,
∴∠AMG=∠HGM,∠CNG=∠HGN,
∵MG⊥NG,
∴∠MGN=∠MGH+∠NGH=∠AMG+∠CNG=90°;
(2)如图2,过G作GK∥AB,过点P作PQ∥AB,设∠GND=α,
∵GK∥AB,AB∥CD,
∴GK∥CD,
∴∠KGN=∠GND=α,
∵GK∥AB,∠BMG=30°,
∴∠MGK=∠BMG=30°,
∵MG平分∠BMP,ND平分∠GNP,
∴∠GMP=∠BMG=30°,
∴∠BMP=60°,
∵PQ∥AB,
∴∠MPQ=∠BMP=60°,
∵ND平分∠GNP,
∴∠DNP=∠GND=α,
∵AB∥CD,
∴PQ∥CD,
∴∠QPN=∠DNP=α,
∴∠MGN=30°+α,∠MPN=60°﹣α,
∴∠MGN+∠MPN=30°+α+60°﹣α=90°;
(3)如图3,过G作GK∥AB,过E作ET∥AB,设∠AMF=x,∠GND=y,
∵AB,FG交于M,MF平分∠AME,
∴∠FME=∠FMA=∠BMG=x,
∴∠AME=2x,
∵GK∥AB,
∴∠MGK=∠BMG=x,
∵ET∥AB,
∴∠TEM=∠EMA=2x,
∵CD∥AB∥KG,
∴GK∥CD,
∴∠KGN=∠GND=y,
∴∠MGN=x+y,
∵∠CND=180°,NE平分∠CNG,
∴∠CNG=180°﹣y,∠CNE=∠CNG=90°﹣y,
∵ET∥AB∥CD,
∴ET∥CD,
∴∠TEN=∠CNE=90°﹣y,
∴∠MEN=∠TEN﹣∠TEM=90°﹣y﹣2x,∠MGN=x+y,
∵2∠MEN+∠G=105°,
∴2(90°﹣y﹣2x)+x+y=105°,
∴x=25°,
∴∠AME=2x=50°.
5.解:(1)∵AB∥ON
∴∠O=∠MCB(两直线平行,同位角相等)
∵∠O=50°
∴∠MCB=50°
∵∠ACM+∠MCB=180°(平角定义)
∴∠ACM=180°﹣50°=130°
又∵CD平分∠ACM
∴∠DCM=65°(角平分线定义)
∴∠BCD=∠DCM+∠MCB=65°+50°=115°
(2)证明:∵CE⊥CD
∴∠DCE=90°
∴∠ACE+∠DCA=90°
又∵∠MCO=180°(平角定义)
∴∠ECO+∠DCM=90°
∵∠DCA=∠DCM
∴∠ACE=∠ECO(等角的余角相等)
即CE平分∠OCA
(3)结论:当∠O=36°或90°时,CA分∠OCD成1:2两部分
①当∠O=36°时
∵AB∥ON
∴∠ACO=∠O=36°
∴∠ACM=144°
又∵CD平分∠ACM
∴∠ACD=72°
∴∠ACO=∠ACD
即CA分∠OCD成1:2两部分
②当∠O=90°时
∵AB∥ON
∴∠ACO=∠O=90°
∴∠ACM=90°
又∵CD平分∠ACM
∴∠ACD=45°
∴∠ACD=∠ACO
即CA分∠OCD成1:2两部分
6.解:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
①当OE平分∠AOB时,∠AOE=45°,
即9°t+30°﹣3°t=45°,
解得t=2.5;
②当OF平分∠AOB时,∠AOF=45°,
即9°t﹣150°﹣3°t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
①当OE平分∠BOD时,∠BOE=∠BOD,
即9°t﹣60°﹣3°t=(60°﹣3°t),
解得t=12;
②当OF平分∠BOD时,∠DOF=∠BOD,
即9°t﹣300°=(3°t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.
7.(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AFH=∠ADC=90°,
∴EF∥DC,
∴∠AHE=∠ACD,
∵∠ACD+∠F=180°.
∴∠AHE+∠F=180°,
∵∠AHE+∠EHC=180°,
∴∠EHC=∠F,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
∴设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴解得x=15°,
∴∠BCD=2x=30°.
答:∠BCD的度数为30°.
8.解:(1)∵DF∥BC,
∴∠ABC=∠ADF=70°,
∵∠ABF=25°,
∴∠CBF=70°﹣25°=45°;
(2)证明:∵DF∥BC,
∴∠ABC=∠ADF,
∵BF平分∠ABC,DE平分∠ADF,
∴∠ADE=ADF,∠ABF=ABC,
∴∠ADE=∠ABF,
∴BF∥DE.
9.证明:(1)∵∠1=52°,∠2=128°,
∴∠1+∠2=180°,
∴BD∥CE;
(2)∵BD∥CE,
∴∠C=∠ABD,
又∵∠C=∠D,
∴∠ABD=∠D,
∵AC∥DF,
∴∠A=∠F.
10.解:∵∠AED=∠C(已知),
∴DE∥BC(同位角相等,两直线平行),
∴∠B+∠BDE=180°
(两直线平行,同旁内角互补),
∵∠DEF=∠B(已知),
∴∠DEF+∠BDE=180°
(等量代换),
∴EF∥AB(同旁内角互补,两直线平行),
∴∠1=∠2
(两直线平行,内错角相等).
故答案为:DE;BC;同位角相等,两直线平行;两直线平行,同旁内角互补;EF;AB;同旁内角互补,两直线平行;两直线平行,内错角相等.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
