小结与思考-特殊四边形

(共17张PPT)
苏科版初中数学九年级上册
第一章 小结与思考
——特殊四边形
南京高淳外国语学校 王忠燕
热身训练

1.平行四边形ABCD中，如果∠A=55°，那么 的度数是（ ）
A.45° B.55° C.125° D.145°
2.已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）
A.当AB=BC时，它是菱形 B.当AC⊥BD时，它是菱形
C.当∠ABC=900时,它是矩形 D.当AC=BD时，它是正方形
3.若等腰梯形的一个底角等于600，它的两底分别为3cm和5cm,则
它的周长为_______cm.
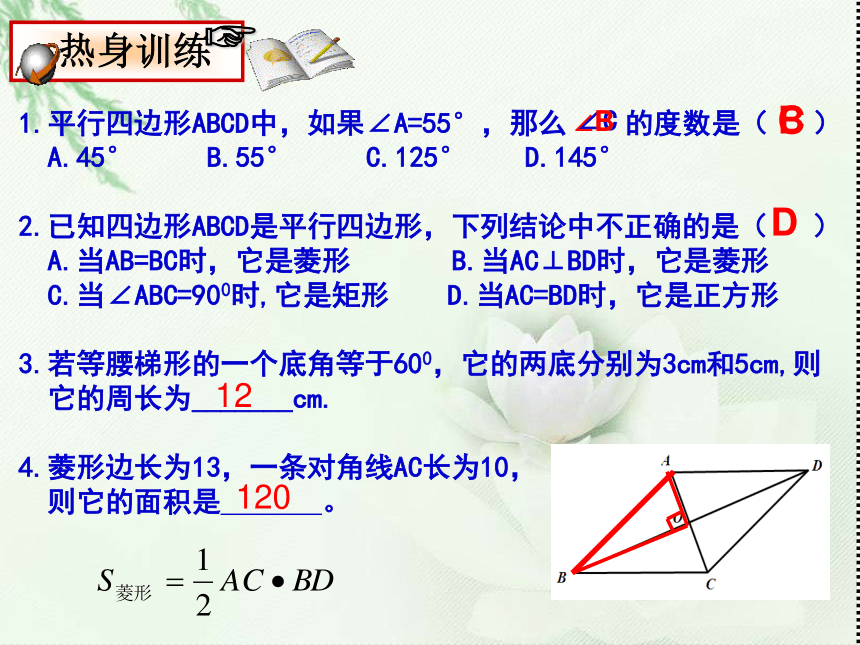
4.菱形边长为13，一条对角线AC长为10，
则它的面积是 。
B
∠C
∠B
C
D
120
12
知识回顾

特殊四边形的关系
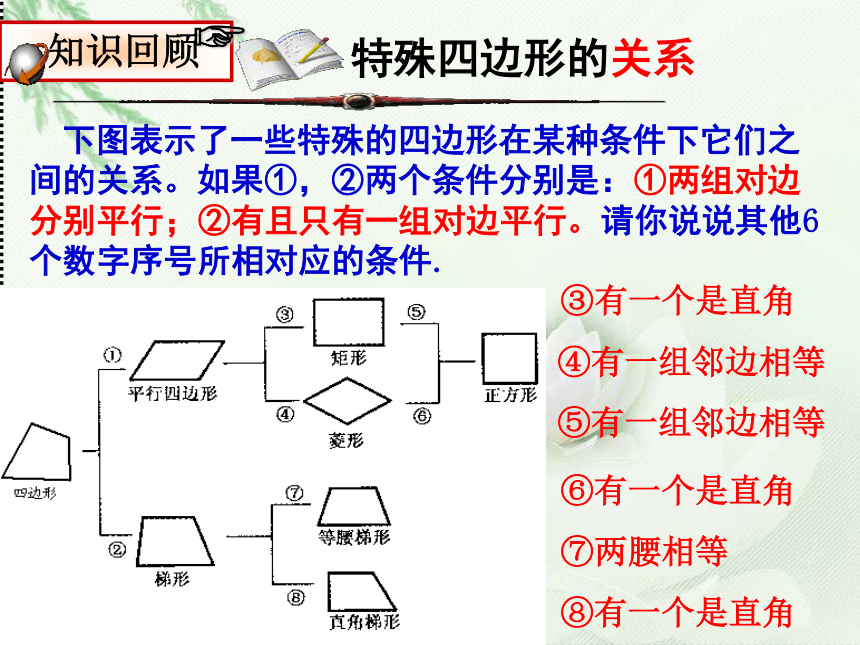
下图表示了一些特殊的四边形在某种条件下它们之间的关系。如果①，②两个条件分别是：①两组对边分别平行；②有且只有一组对边平行。请你说说其他6个数字序号所相对应的条件.
③有一个是直角
④有一组邻边相等
⑥有一个是直角
⑤有一组邻边相等
⑦两腰相等
⑧有一个是直角
知识回顾

特殊四边形的性质
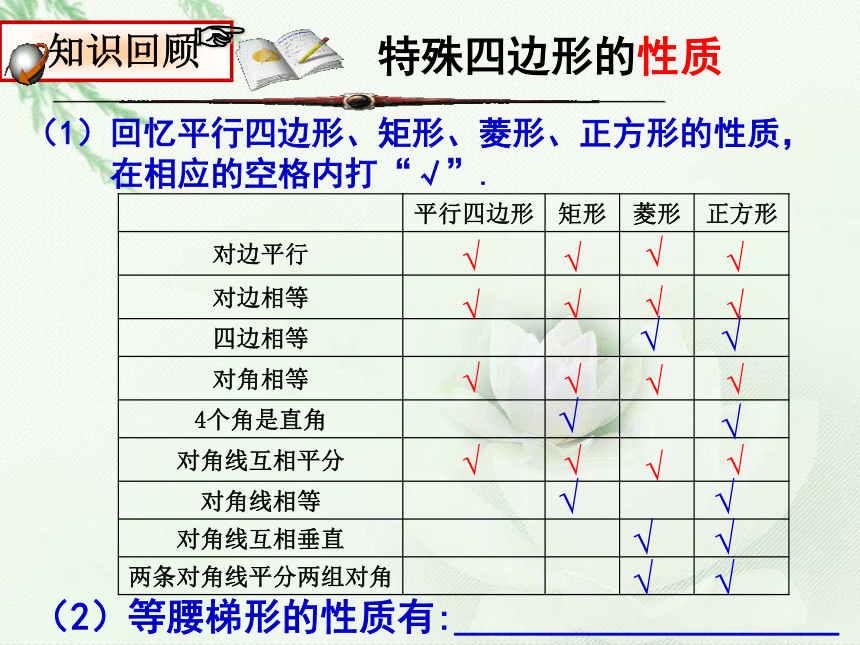
（1）回忆平行四边形、矩形、菱形、正方形的性质，
在相应的空格内打“√”.
平行四边形 矩形 菱形 正方形
对边平行
对边相等
四边相等
对角相等
4个角是直角
对角线互相平分
对角线相等
对角线互相垂直
两条对角线平分两组对角
（2）等腰梯形的性质有:____________________
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
知识回顾

特殊四边形的判定
四边形 判定条件
平行四边形
矩形
菱形
正方形
等腰梯形
(1)两组对边分别平行;
(2)两组对边分别相等;
(3)一组对边平行且相等;
(4)对角线互相平分.
(1)有三个角是直角;
(2)一个角是直角+平行四边形;
(3)对角线相等+平行四边形.
(1)四边都相等;
(2)一组邻边相等+平行四边形;
(3)对角线互相垂直+平行四边形.
(2)一组邻边相等+矩形;
(1)一组邻边相等+一个角是直角+平行四边形;
(3)一个角是直角+菱形.
(1)两腰相等+梯形
(2)同一底上两个底角相等+梯形
平行四边形:
(1)两组对边分别平行
(2)两组对边分别相等
(3)一组对边平行且相等
(4)对角线互相平分
知识回顾

特殊四边形的判定
知识回顾

特殊四边形的判定
矩形:
(1)有三个角是直角;
(2)一个角是直角+平行四边形;
(3)对角线相等+平行四边形.
知识回顾

特殊四边形的判定
菱形:
(1)四边都相等;
(2)一组邻边相等+平行四边形;
(3)对角线互相垂直+平行四边形.
知识回顾

特殊四边形的判定
正方形:
(2)一组邻边相等+矩形;
(1)一组邻边相等+一个角是直角
+平行四边形;
(3)一个角是直角+菱形.
典例分析

例1.已知：四边形ABCD中，AB∥CD，要使四边形ABCD为平行四边形，需添加一个条件 ，并说明理由。
例2．如图，在△ABC中，点O是AC边上的一个动点（点O不与A、C两点重合），过点O作直线MN∥BC，直线MN与∠BCA的平分线相交于点E，与∠DCA（△ABC的外角）的平分线相交于点F．
典例分析

(1)OE与OF相等吗？为什么？
解：(1) OE=OF
理由：∵MN ∥BC
又∵ CE平分∠BCA
∴ ∠1= ∠3
∴ OE= OC
同理 OF= OC
∴ OE= OF
∴ ∠1= ∠2
∴ ∠2= ∠3
1
2
3
例2．如图，在△ABC中，点O是AC边上的一个动点（点O不与A、C两点重合），过点O作直线MN∥BC，直线MN与∠BCA的平分线相交于点E，与∠DCA（△ABC的外角）的平分线相交于点F．
典例分析

(2)探究：当点O运动到何处时，四边形AECF是矩形？并证明你的结论．
(2)当点O位于AC的中点时，四边形AECF是矩形
证明： ∵ O为AC的中点 ∴ A0=CO
由（1）得 OE=OF
∴ 四边形AECF是平行四边形
3
4
又∵ CE平分∠BCA，CF平分∠DCA
∴ ∠3= ∠BCA, ∠4= ∠DCA
∴ ∠3+ ∠4= ( ∠BCA +∠DCA)= 1800=900
×
即∠ECF=900
∴ □ AECF是矩形
例2．如图，在△ABC中，点O是AC边上的一个动点（点O不与A、C两点重合），过点O作直线MN∥BC，直线MN与∠BCA的平分线相交于点E，与∠DCA（△ABC的外角）的平分线相交于点F．
典例分析

(3)在(2)中，当∠ACB等于多少时，四边形AECF为正方形．(不要求说理由)
巩固练习

1.如图，AD是△ABC的高，DE∥AC，DF∥AB，则△ABC满足条件 时，四边形AEDF是菱形。
巩固练习

2.如图，在△ABC中，D是BC边上的一点，点E是AD的中点，过点A作AF//BC交CE的延长线于点F，且AF=BD，连接BF，
（1）说明：BD=CD；
（2）如果AB=AC，试判断四边形AFBD的形状，并证明你
的结论。
（3）在第（2）问的条件下再给△ABC添加一个条件，
使四边形AFBD为正方形。
通过本堂课的学习，
说说你的收获和体会
课后作业
必做题：P37 3.4.5.7
选做题：P39 15