2020-2021学年七年级数学北师大版下册2.1两条直线的位置关系 同步习题(word版,含答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册2.1两条直线的位置关系 同步习题(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 93.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-01 23:39:05 | ||
图片预览


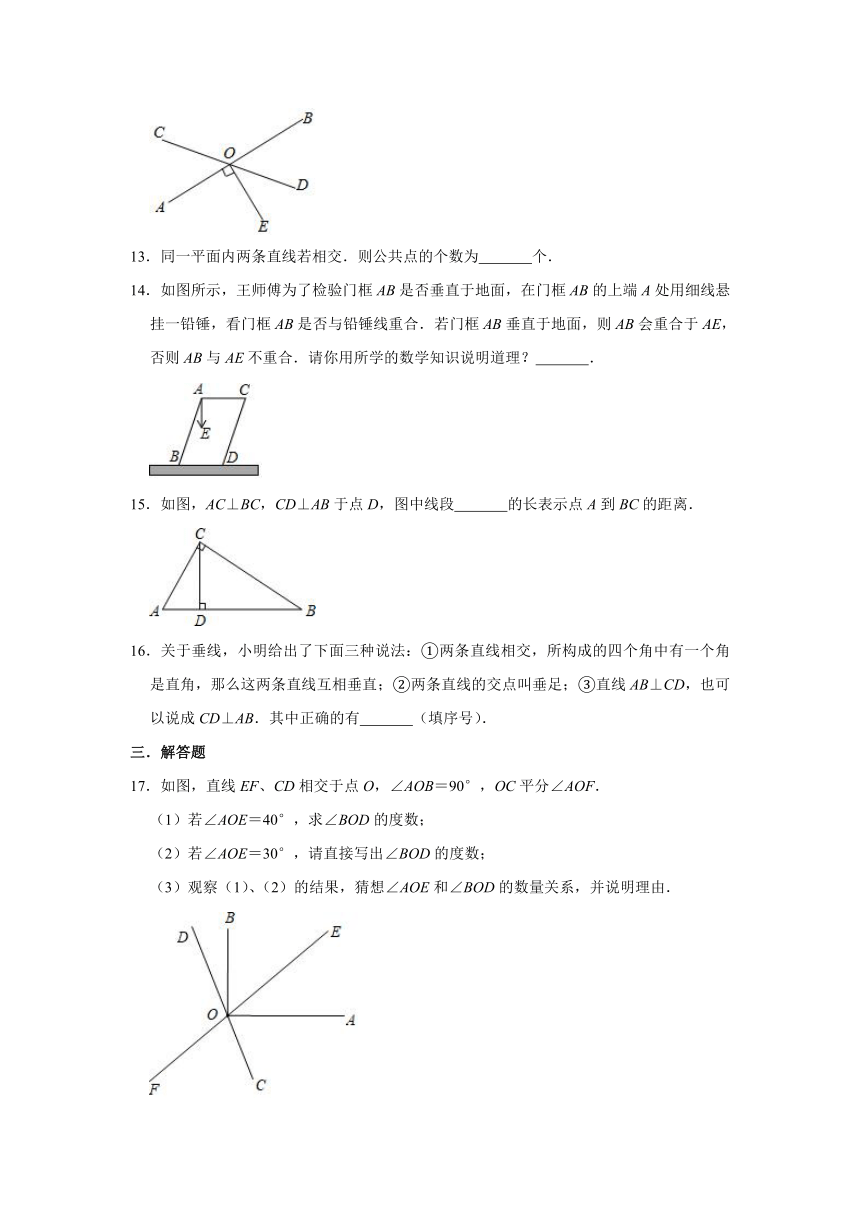

文档简介
2.1两条直线的位置关系 同步习题
一.选择题
1.下列四个图中,∠1=∠2一定成立的是( )
A. B. C. D.
2.下列说法中,正确的是( )
A.从直线外一点到这条直线的垂线段,叫做这个点到这条直线的距离
B.互相垂直的两条直线一定相交
C.直线AB外一点P与直线上各点连接而成的所有线段中最短线段的长是7cm,则点P到直线AB的距离是7cm
D.有且只有一条直线垂直于已知直线
3.如图所示,已知AB和CD相交于点O,OE⊥AB于点O,如果∠COE=70°,则∠AOD=( )
A.30° B.20° C.25° D.15°
4.如图,PO⊥OR,OQ⊥PR,则点O到PR所在直线的距离是线段( )的长.
A.OQ B.OR C.OP D.PQ
5.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.4 B.5 C.6 D.以上都不对
6.如图所示,AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
A.两点确定一条直线
B.过一点能作一条垂线
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
7.下列图形中,∠1与∠2互为邻补角的是( )
A. B.
C. D.
8.在同一平面内的n条直线两两相交,最多共有36个交点,则n=( )
A.7 B.8 C.9 D.10
9.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,若∠EOC=20°,则∠DOB的度数为( )
A.70° B.90° C.110° D.120°
10.若点P为直线l外一定点,点A为直线l上一定点,且PA=2,点P到直线l的距离为d,则d的取值范围为( )
A.0<d<2 B.d=2或d>2 C.0<d<2或d=0 D.0<d<2或d=2
二.填空题
11.三条直线两两相交共有 对邻补角.
12.如图,直线AB、CD相交于点O,OE⊥AB于O,∠AOC=56°,则∠DOE= .
13.同一平面内两条直线若相交.则公共点的个数为 个.
14.如图所示,王师傅为了检验门框AB是否垂直于地面,在门框AB的上端A处用细线悬挂一铅锤,看门框AB是否与铅锤线重合.若门框AB垂直于地面,则AB会重合于AE,否则AB与AE不重合.请你用所学的数学知识说明道理? .
15.如图,AC⊥BC,CD⊥AB于点D,图中线段 的长表示点A到BC的距离.
16.关于垂线,小明给出了下面三种说法:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直;②两条直线的交点叫垂足;③直线AB⊥CD,也可以说成CD⊥AB.其中正确的有 (填序号).
三.解答题
17.如图,直线EF、CD相交于点O,∠AOB=90°,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)、(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
18.如图,两条直线a,b相交.
(1)如果∠1=50°,求∠2,∠3的度数;
(2)如果∠2=3∠1,求∠3,∠4的度数.
19.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
参考答案
一.选择题
1.解:A选项中,∠1+∠2=180°,不能判定∠1≠∠2,故不符合题意;
B选项中,∠1和∠2是对顶角,故∠1=∠2,故符合题意;
C选项中,只有两条被截直线平行时,∠1=∠2,故不符合题意;
D选项中,无法判断∠1=∠2,故不符合题意.
故选:B.
2.解:A.从直线外一点到这条直线的垂线段的长度,叫这个点到这条直线的距离,故本选项不符合题意;
B.如图:
直线AD⊥直线GH,但是AD和GH不相交,故本选项不符合题意;
C.根据点到直线的距离的定义可知:此时的7cm就是点P到直线AB的距离,故本选项符合题意;
D.如图:
直线a的垂线有无数条,故本选项不符合题意;
故选:C.
3.解:∵OE⊥AB,
∴∠BOE=90°,
∵∠COE=70°,
∴∠BOC=∠BOE﹣∠COE=90°﹣70°=20°,
∴∠AOD=∠BOC=20°,
故选:B.
4.解:∵OQ⊥PR,
∴点O到PR所在直线的距离是线段OQ的长.
故选:A.
5.解:根据题意可得:3条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,3条直线相交,交点最多为3个,即n=3;
则m+n=1+3=4.
故选:A.
6.解:
因为 AB⊥l,BC⊥l,B 为垂足,所以 AB 和 BC 重合,其理由是:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
故选:D.
7.解:A.两个角不等于180°,故不是邻补角;
B、两个角是对顶角,故不是邻补角;
C、两个角不存在公共边,故不是邻补角;
D、两个角是邻补角,符合题意.
故选:D.
8.解:2条直线相交最多有1个交点;
3条直线相交最多有1+2个交点;
4条直线相交最多有1+2+3个交点;
5条直线相交最多有1+2+3+4个交点;
6条直线相交最多有1+2+3+4+5个交点;
…
所以n条直线相交最多有1+2+3+4+5+…+(n﹣1)=个交点;
由题意得=36,
解得n=9.
故选:C.
9.解:∵OE⊥AB,
∴∠BOE=90°,
∵∠EOC=20°,
∴∠BOC=∠BOE﹣∠EOC=90°﹣20°=70°,
∴∠DOB=180°﹣∠BOC=180°﹣70°=110°.
故选:C.
10.解:∵点P为直线l外一定点,点A为直线l上一定点,且PA=2,
∴点P到直线l的距离d的取值范围为:0<d<2或d=2,
故选:D.
二.填空题
11.解:如图
三条直线两两相交,每个交点有4对邻补角,共有12对邻补角.
故答案为:12.
12.解:∵∠AOC=56°,
∴∠BOD=56°,
∵OE⊥AB于O,
∴∠BOE=90°,
∴∠DOE=90°﹣56°=34°,
故答案为:34°.
13.解:同一平面内两条直线若相交.则公共点的个数为1个,
故答案为:1.
14.解:王师傅为了检验门框AB是否垂直于地面,在门框AB的上端A处用细线悬挂一铅锤,看门框AB是否与铅锤线重合.若门框AB垂直于地面,则AB会重合于AE,否则AB与AE不重合.所用的数学知识是:在同一平面内,过一点有且只有一条直线与已知直线垂直.
故答案为:在同一平面内,过一点有且只有一条直线与已知直线垂直.
15.解:由AC⊥BC于C可得,线段AC的长表示点A到BC的距离.
故答案为:AC.
16.解:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直,故原题说法正确;
②两条直线的交点叫交点,故原题说法错误;
③直线AB⊥CD,也可以说成CD⊥AB,故原题说法正确,
正确的说法有2个,
故答案为:①③.
三.解答题
17.解:(1)∵∠AOE+∠AOF=180°,∠AOE=40°,
∴∠AOF=180°﹣∠AOE=140°
∵OC平分∠AOF,
∴∠AOC=∠AOF=×140°=70°
∵∠AOB=90°
∴∠BOD=180°﹣∠AOC﹣∠AOB=180°﹣70°﹣90°=20°
(2)方法同(1)可得,若∠AOE=30°,则∠BOD=15°
(3)猜想:∠BOD=∠AOE,
理由如下:
∵OC平分∠AOF
∴∠AOC=∠AOF
∵∠AOE+∠AOF=180°,
∴∠AOF=180°﹣∠AOE
∵∠BOD+∠AOB+∠AOC=180°,∠AOB=90°
∴∠BOD+90°+∠AOF=180°,
∴∠BOD=90°﹣∠AOF=90°﹣90°+∠AOE=∠AOE.
18.解:(1)∵∠1=50°,∠1+∠2=180°,
∴∠2=180°﹣50°=130°,
又∵∠3与∠1是对顶角,
∴∠3=∠1=50°;
(2)∵∠2=3∠1,∠1+∠2=180°,
∴∠1+3∠1=180°,
∴4∠1=180°,
∴∠1=45°,
∴∠3=∠1=45°,
又∠1+∠4=180°,
∴∠4=180°﹣∠1=180°﹣45°=135°.
19.解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
一.选择题
1.下列四个图中,∠1=∠2一定成立的是( )
A. B. C. D.
2.下列说法中,正确的是( )
A.从直线外一点到这条直线的垂线段,叫做这个点到这条直线的距离
B.互相垂直的两条直线一定相交
C.直线AB外一点P与直线上各点连接而成的所有线段中最短线段的长是7cm,则点P到直线AB的距离是7cm
D.有且只有一条直线垂直于已知直线
3.如图所示,已知AB和CD相交于点O,OE⊥AB于点O,如果∠COE=70°,则∠AOD=( )
A.30° B.20° C.25° D.15°
4.如图,PO⊥OR,OQ⊥PR,则点O到PR所在直线的距离是线段( )的长.
A.OQ B.OR C.OP D.PQ
5.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.4 B.5 C.6 D.以上都不对
6.如图所示,AB⊥l,BC⊥l,B为垂足,所以AB和BC重合,其理由是( )
A.两点确定一条直线
B.过一点能作一条垂线
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
7.下列图形中,∠1与∠2互为邻补角的是( )
A. B.
C. D.
8.在同一平面内的n条直线两两相交,最多共有36个交点,则n=( )
A.7 B.8 C.9 D.10
9.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,若∠EOC=20°,则∠DOB的度数为( )
A.70° B.90° C.110° D.120°
10.若点P为直线l外一定点,点A为直线l上一定点,且PA=2,点P到直线l的距离为d,则d的取值范围为( )
A.0<d<2 B.d=2或d>2 C.0<d<2或d=0 D.0<d<2或d=2
二.填空题
11.三条直线两两相交共有 对邻补角.
12.如图,直线AB、CD相交于点O,OE⊥AB于O,∠AOC=56°,则∠DOE= .
13.同一平面内两条直线若相交.则公共点的个数为 个.
14.如图所示,王师傅为了检验门框AB是否垂直于地面,在门框AB的上端A处用细线悬挂一铅锤,看门框AB是否与铅锤线重合.若门框AB垂直于地面,则AB会重合于AE,否则AB与AE不重合.请你用所学的数学知识说明道理? .
15.如图,AC⊥BC,CD⊥AB于点D,图中线段 的长表示点A到BC的距离.
16.关于垂线,小明给出了下面三种说法:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直;②两条直线的交点叫垂足;③直线AB⊥CD,也可以说成CD⊥AB.其中正确的有 (填序号).
三.解答题
17.如图,直线EF、CD相交于点O,∠AOB=90°,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)、(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
18.如图,两条直线a,b相交.
(1)如果∠1=50°,求∠2,∠3的度数;
(2)如果∠2=3∠1,求∠3,∠4的度数.
19.如图所示,码头、火车站分别位于A,B两点,直线a和b分别表示铁路与河流.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
参考答案
一.选择题
1.解:A选项中,∠1+∠2=180°,不能判定∠1≠∠2,故不符合题意;
B选项中,∠1和∠2是对顶角,故∠1=∠2,故符合题意;
C选项中,只有两条被截直线平行时,∠1=∠2,故不符合题意;
D选项中,无法判断∠1=∠2,故不符合题意.
故选:B.
2.解:A.从直线外一点到这条直线的垂线段的长度,叫这个点到这条直线的距离,故本选项不符合题意;
B.如图:
直线AD⊥直线GH,但是AD和GH不相交,故本选项不符合题意;
C.根据点到直线的距离的定义可知:此时的7cm就是点P到直线AB的距离,故本选项符合题意;
D.如图:
直线a的垂线有无数条,故本选项不符合题意;
故选:C.
3.解:∵OE⊥AB,
∴∠BOE=90°,
∵∠COE=70°,
∴∠BOC=∠BOE﹣∠COE=90°﹣70°=20°,
∴∠AOD=∠BOC=20°,
故选:B.
4.解:∵OQ⊥PR,
∴点O到PR所在直线的距离是线段OQ的长.
故选:A.
5.解:根据题意可得:3条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,3条直线相交,交点最多为3个,即n=3;
则m+n=1+3=4.
故选:A.
6.解:
因为 AB⊥l,BC⊥l,B 为垂足,所以 AB 和 BC 重合,其理由是:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
故选:D.
7.解:A.两个角不等于180°,故不是邻补角;
B、两个角是对顶角,故不是邻补角;
C、两个角不存在公共边,故不是邻补角;
D、两个角是邻补角,符合题意.
故选:D.
8.解:2条直线相交最多有1个交点;
3条直线相交最多有1+2个交点;
4条直线相交最多有1+2+3个交点;
5条直线相交最多有1+2+3+4个交点;
6条直线相交最多有1+2+3+4+5个交点;
…
所以n条直线相交最多有1+2+3+4+5+…+(n﹣1)=个交点;
由题意得=36,
解得n=9.
故选:C.
9.解:∵OE⊥AB,
∴∠BOE=90°,
∵∠EOC=20°,
∴∠BOC=∠BOE﹣∠EOC=90°﹣20°=70°,
∴∠DOB=180°﹣∠BOC=180°﹣70°=110°.
故选:C.
10.解:∵点P为直线l外一定点,点A为直线l上一定点,且PA=2,
∴点P到直线l的距离d的取值范围为:0<d<2或d=2,
故选:D.
二.填空题
11.解:如图
三条直线两两相交,每个交点有4对邻补角,共有12对邻补角.
故答案为:12.
12.解:∵∠AOC=56°,
∴∠BOD=56°,
∵OE⊥AB于O,
∴∠BOE=90°,
∴∠DOE=90°﹣56°=34°,
故答案为:34°.
13.解:同一平面内两条直线若相交.则公共点的个数为1个,
故答案为:1.
14.解:王师傅为了检验门框AB是否垂直于地面,在门框AB的上端A处用细线悬挂一铅锤,看门框AB是否与铅锤线重合.若门框AB垂直于地面,则AB会重合于AE,否则AB与AE不重合.所用的数学知识是:在同一平面内,过一点有且只有一条直线与已知直线垂直.
故答案为:在同一平面内,过一点有且只有一条直线与已知直线垂直.
15.解:由AC⊥BC于C可得,线段AC的长表示点A到BC的距离.
故答案为:AC.
16.解:①两条直线相交,所构成的四个角中有一个角是直角,那么这两条直线互相垂直,故原题说法正确;
②两条直线的交点叫交点,故原题说法错误;
③直线AB⊥CD,也可以说成CD⊥AB,故原题说法正确,
正确的说法有2个,
故答案为:①③.
三.解答题
17.解:(1)∵∠AOE+∠AOF=180°,∠AOE=40°,
∴∠AOF=180°﹣∠AOE=140°
∵OC平分∠AOF,
∴∠AOC=∠AOF=×140°=70°
∵∠AOB=90°
∴∠BOD=180°﹣∠AOC﹣∠AOB=180°﹣70°﹣90°=20°
(2)方法同(1)可得,若∠AOE=30°,则∠BOD=15°
(3)猜想:∠BOD=∠AOE,
理由如下:
∵OC平分∠AOF
∴∠AOC=∠AOF
∵∠AOE+∠AOF=180°,
∴∠AOF=180°﹣∠AOE
∵∠BOD+∠AOB+∠AOC=180°,∠AOB=90°
∴∠BOD+90°+∠AOF=180°,
∴∠BOD=90°﹣∠AOF=90°﹣90°+∠AOE=∠AOE.
18.解:(1)∵∠1=50°,∠1+∠2=180°,
∴∠2=180°﹣50°=130°,
又∵∠3与∠1是对顶角,
∴∠3=∠1=50°;
(2)∵∠2=3∠1,∠1+∠2=180°,
∴∠1+3∠1=180°,
∴4∠1=180°,
∴∠1=45°,
∴∠3=∠1=45°,
又∠1+∠4=180°,
∴∠4=180°﹣∠1=180°﹣45°=135°.
19.解:如图所示
(1)沿AB走,两点之间线段最短;
(2)沿AC走,垂线段最短;
(3)沿BD走,垂线段最短.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
