3.2一元二次不等式课件(苏教版必修5)
文档属性
| 名称 | 3.2一元二次不等式课件(苏教版必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 600.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-30 00:00:00 | ||
图片预览




文档简介
(共11张PPT)
一元二次不等式
引入:
5x2-10x+4.8<0 ②
一元二次不等式:
一元二次方程:
5x2-10x+4.8=0 ③
y=5x2-10x+4.8 ④
0.8
1.2
x
y
0
由图像可看出:
当y=0时,
X=0.8或x=1.2;
当y>0时,
X<0.8或x>1.2;
0.8一元二次函数:
当y<0时,
5x2-10x+4.8 ﹥0 ①
思考1:一元二次方程、一元二次不等式与相应的一元二次函数之间有什么内在联系
(1)、一元二次方程ax2+bx+c=0的根即是一元二次函数y=ax2+bx+c的图像与x轴交点的横坐标;
(2)、一元二次不等式ax2+bx+c﹥0(a ﹥0)的解集即是一元二次函y=ax2+bx+c的图像(抛物线)位于x轴上方的点所对应的x值的集合。(3)……
归纳1:解不等式5x2-10x+4.8<0步骤?
示例:解不等式5x2-10x+4.8<0
解:解方程5x2-10x+4.8=0得:
x1=0.8,x2=1.2
作出函数y=5x2-10x+4.8的草图
如图所示。
0.8
1.2
x
y
0
所以不等式5x2-10x+4.8<0的解集为:
(1)…..
(2)…..
(3)…..
2、上面这种利用对应的二次函数的图像解一元二次不等式的方法叫图像法。
例1、解下列不等式
(1) x2-7x+12>0; (2) -x2-2x+3 ≥ 0;
(3) x2-2x+1<0; (4) x2-2x+2<0.
反思:求解一元二次不等式首先要看对应一元二次方程根的情况!
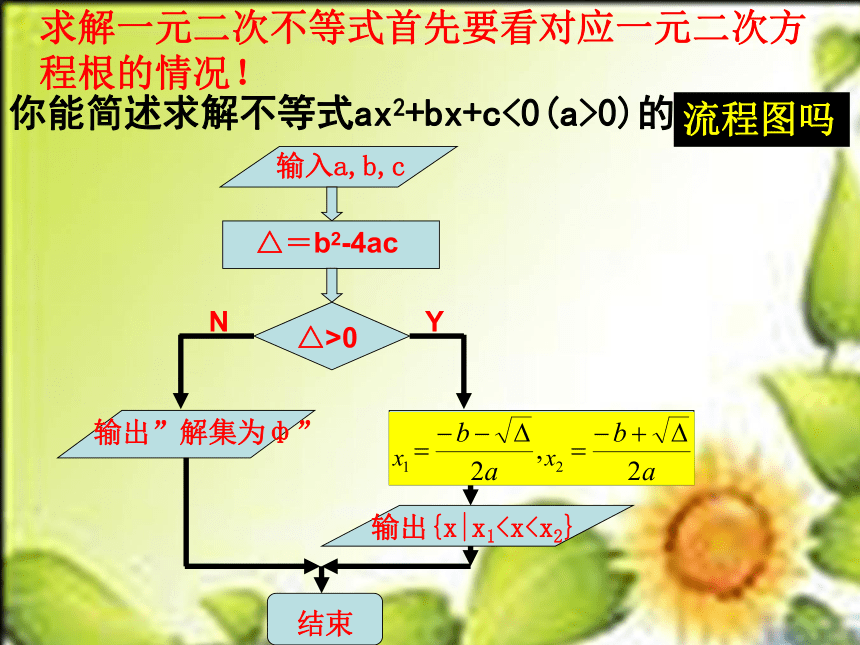
求解一元二次不等式首先要看对应一元二次方程根的情况!
你能简述求解不等式ax2+bx+c<0(a>0)的步骤吗?
流程图吗
输入a,b,c
△=b2-4ac
△>0
N
输出”解集为ф”
Y
输出{x|x1结束
方程:ax2+bx+c=0的解情况 函数:
y=ax2+bx+c 的图象 不等式的解集
ax2+bx+c>0 ax2+bx+c<0
a>0
x
y
o
x1
x2
x
o
x0
y
x
o
y
当⊿>0时,方程有两不等的根x1 ,x2
当⊿=0 时,方程有两相等的根
X1=X2=x0
当⊿<0 时,方程无解
{x∣x<x1
或 x>x2}
{ x∣x≠x0}
R
{x∣x1<x<x2 }
大于取两边
小于取中间
若a<0呢
练习:
1、2 、3、4
说明:数形结合要牢记心中,但书写过程可简化。
解不等式:2x2-5x+3<0
解:因为,原不等式可化为
(2x-3)(x-1)<0
所以原不等式的解集是{x|11.化不等式为标准式ax2+bx+c>0或ax2+bx+c0)
3.根据图象写出不等式的解集
例2:解关于x的不等式x2-(a+1)x+a>0
变形1:解关于x的不等式 x2-ax - (a+1) >0 (a≠0)
引申1:解关于x的不等式 ax2-(a+1)x+1>0 (a≠0)
分类讨论!
变形2:求函数 的定义域。
引申2:若 的定义域为R,求b范围。
拓展:若 的值域为R,求b范围。
R
-12
-2
-2≤a≤6
思考题:
作业:第1、2题
一元二次不等式
引入:
5x2-10x+4.8<0 ②
一元二次不等式:
一元二次方程:
5x2-10x+4.8=0 ③
y=5x2-10x+4.8 ④
0.8
1.2
x
y
0
由图像可看出:
当y=0时,
X=0.8或x=1.2;
当y>0时,
X<0.8或x>1.2;
0.8
当y<0时,
5x2-10x+4.8 ﹥0 ①
思考1:一元二次方程、一元二次不等式与相应的一元二次函数之间有什么内在联系
(1)、一元二次方程ax2+bx+c=0的根即是一元二次函数y=ax2+bx+c的图像与x轴交点的横坐标;
(2)、一元二次不等式ax2+bx+c﹥0(a ﹥0)的解集即是一元二次函y=ax2+bx+c的图像(抛物线)位于x轴上方的点所对应的x值的集合。(3)……
归纳1:解不等式5x2-10x+4.8<0步骤?
示例:解不等式5x2-10x+4.8<0
解:解方程5x2-10x+4.8=0得:
x1=0.8,x2=1.2
作出函数y=5x2-10x+4.8的草图
如图所示。
0.8
1.2
x
y
0
所以不等式5x2-10x+4.8<0的解集为:
(1)…..
(2)…..
(3)…..
2、上面这种利用对应的二次函数的图像解一元二次不等式的方法叫图像法。
例1、解下列不等式
(1) x2-7x+12>0; (2) -x2-2x+3 ≥ 0;
(3) x2-2x+1<0; (4) x2-2x+2<0.
反思:求解一元二次不等式首先要看对应一元二次方程根的情况!
求解一元二次不等式首先要看对应一元二次方程根的情况!
你能简述求解不等式ax2+bx+c<0(a>0)的步骤吗?
流程图吗
输入a,b,c
△=b2-4ac
△>0
N
输出”解集为ф”
Y
输出{x|x1
方程:ax2+bx+c=0的解情况 函数:
y=ax2+bx+c 的图象 不等式的解集
ax2+bx+c>0 ax2+bx+c<0
a>0
x
y
o
x1
x2
x
o
x0
y
x
o
y
当⊿>0时,方程有两不等的根x1 ,x2
当⊿=0 时,方程有两相等的根
X1=X2=x0
当⊿<0 时,方程无解
{x∣x<x1
或 x>x2}
{ x∣x≠x0}
R
{x∣x1<x<x2 }
大于取两边
小于取中间
若a<0呢
练习:
1、2 、3、4
说明:数形结合要牢记心中,但书写过程可简化。
解不等式:2x2-5x+3<0
解:因为,原不等式可化为
(2x-3)(x-1)<0
所以原不等式的解集是{x|1
3.根据图象写出不等式的解集
例2:解关于x的不等式x2-(a+1)x+a>0
变形1:解关于x的不等式 x2-ax - (a+1) >0 (a≠0)
引申1:解关于x的不等式 ax2-(a+1)x+1>0 (a≠0)
分类讨论!
变形2:求函数 的定义域。
引申2:若 的定义域为R,求b范围。
拓展:若 的值域为R,求b范围。
R
-12
-2
-2≤a≤6
思考题:
作业:第1、2题
