浙江省宁波市宁海中学创新班2021届高三下学期2月测试数学试题 Word版含答案
文档属性
| 名称 | 浙江省宁波市宁海中学创新班2021届高三下学期2月测试数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 790.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-02 00:00:00 | ||
图片预览




文档简介
2021年2月宁海中学创新班测试卷
1. 已知集合false,false,则( )
A. false B. false C. false D. false
2. 复数false(false为虚数单位)的共轭复数是( )
A. false B. false C. false D. false
3. 某几何体的三视图如图所示,则该几何体的体积是( )
A. false B. false C. false D. false
4. 函数false的图像可能是( )
A. B.
C. D.
5. 若实数false,false满足约束条件false,则false的取值范围是( )
A. false B. false C. false D. false
6. 小智参加三分投篮比赛,投中1次得1分,投不中扣1分,已知小智投篮命中率为0.5,记小智投篮三次后的得分为随机变量false,则false为( )
A. false B. false C. false D. 3
7. 已知数列false为等差数列,则“false为有理数”是“数列false中存在有理数” ( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
8. 已知平面向量false,false满足false,false,且false,则false的最小值是( )
A. false B. false C. false D. false
9. 如图,在false中,false,false,点false为线段false上一点,将false绕false翻折,若在翻折过程中存在某位置,使得false,记false为false的最小值.则( )
A. false B. false
C. false D. false
10. 记false(false为自然对数的底数),若对任意false,存在不等实数false,使得false,则满足条件的整数false的个数是( )
A. 2 B. 3 C. 4 D. 5
11. 早在两千多年前,我国的墨子给出了圆的定义“一中同长也”已知false为坐标原点,false,若false,false的“长”分别为1,false,且两圆相切,则false_________.
12. 二项式false的展开式中有_____________项有理项;这些项的系数之和是__________.
13. 在false中,角false,false,false所对的边分别为false,false,false,若false,false,false,则false_________;false的面积是__________.
14. 若定义在false上的偶函数满足false,false,则false___________﹔若实数false,false满足false,设函数false,则false在false上最少有____________个零点.
15. 已知椭圆false的左,右焦点分别为false,false,点false为直线false上的一个动点(不在坐标轴上),则当false的最大值为false时,椭圆的离心率是_________.
16. 如图,在false的点阵中,依次随机地选出false,false,false三个点,则选出的三点满足的概率是false的概率是___________;单调递增区间是__________.
18. 已知函数false.
(1)求函数false的振幅与单调区间;
(2)在false中,false为锐角,满足false,若false,求false.
19. 如图,已知四棱锥false中,false平面false,平面false平面false,且false,false,false,点false在平面false内的射影恰为false的重心false.
(1)证明:false;
(2)求直线false与平面false所成角的正弦值.
20. 已知数列false满足:false,false.
(Ⅰ)求数列false的通项公式;
(Ⅱ)若数列false满足数列false前false项和为false,求数列false的前false项和.
21. 已知椭圆false的离心率为false,过false作斜率为false的直线false交椭圆于false,false两点,false,false,false互不重合.
(Ⅰ)对于给定的false,若false,求false的取值范围(星空专用)(用false表示);
(Ⅱ)对于给定的false满足false(false且false),当false(false为坐标原点)的面积最大时,求椭圆的标准方程(用false表示).
22. 已知函数false,false.
(Ⅰ)若false,false是false的两个根,证明:false;
(Ⅱ)若存在false,使false,求false的取值范围.
2021年2月宁海中学创新班测试卷
1-5:DBADA 6-10:BABCD
11. 1 12. 3,225 13. 4,false 14. 所以至少2个零点
15. 设false到false轴的距离为false,
则falsefalse,解得:false.
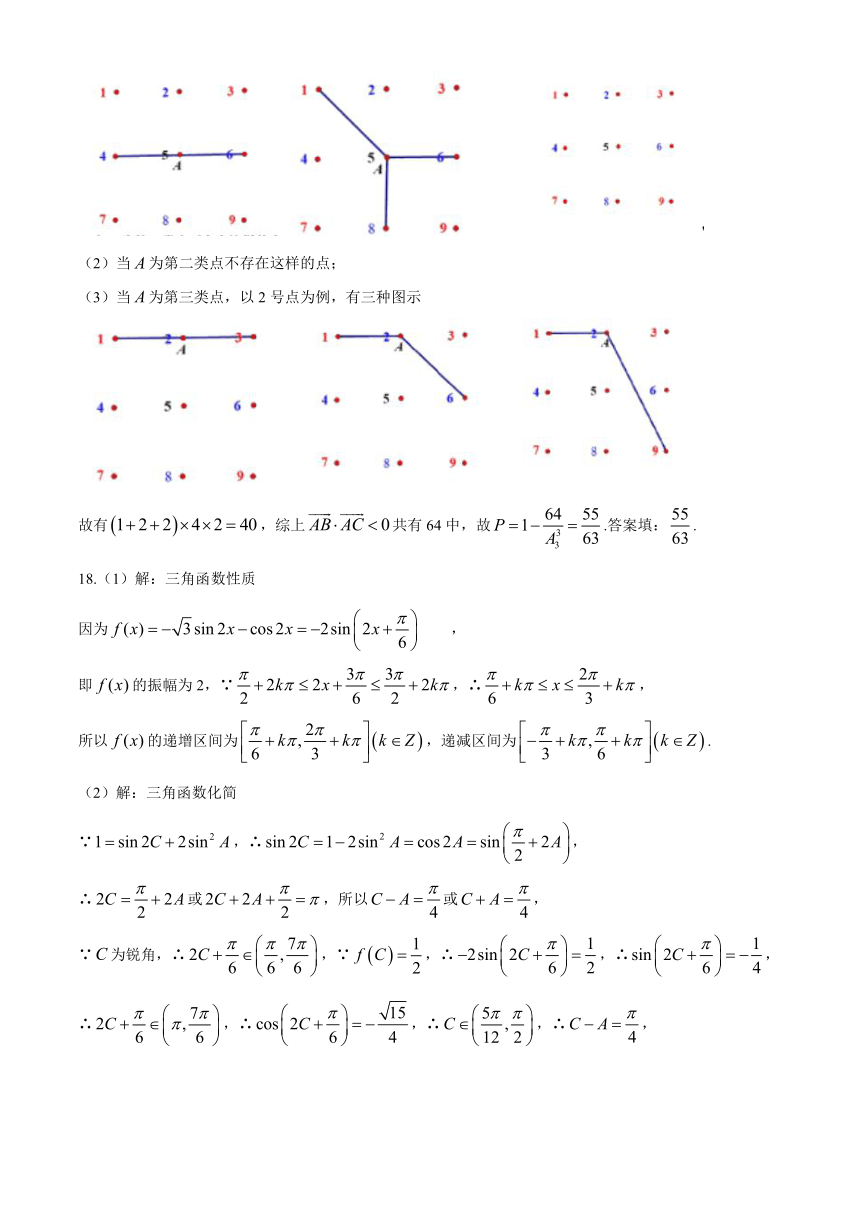
16. 由题意可知false,false,false三个点是有序的,从反面false的角度做,讨论的是false为主元,
故对false分三种情况讨论,如图:第一类false为5号点;第二类false为1,3,7,9号点;
第三类false为2,4,6,8号点;
(1)当false为5号点时,则(i)false,三点共线有四条直线,故false,
(ii)false,则,如false在1号位,false和false即false,共有false,共有false种.
'
(2)当false为第二类点不存在这样的点;
(3)当false为第三类点,以2号点为例,有三种图示
故有false,综上false共有64中,故false.答案填:false.
18.(1)解:三角函数性质
因为false,
即false的振幅为2,∵false,∴false,
所以false的递增区间为false,递减区间为false.
(2)解:三角函数化简
∵false,∴false,
∴false或false,所以false或false,
∵false为锐角,∴false,∵false,∴false,∴false,
∴false,∴false,∴false,∴false,
∴false
false
false.
19. 解:(1)过false作false于false,因为平面false平面false,平面false平面false,false平面false,所以false平面false,∴false.因为false平面false,所以false,false,所以false平面false,∴false.
(2)连结false并延长交false于false,连结false.以false为原点,分别以false,false所在的直线为false,false轴,以过false且与平面false垂直的直线为false轴,建立空间直角坐标系,如图所示,则false,false,false,设false,∵false平面false,∴false,同理false,∴false,∴false平面false,∴false,∵false是false的重心,∴false是false的中点,∴false,由(1)知,false,∴false,∴false,false,∴false,∴false,∴false,设false,则false,故false,∴false,false,
∴false,∴false,∴false,∴false,false,false,设平面false的法向量为false,则false,false,令false,则false,设直线false与平面false所成角为false,则falsefalse,故直线false与平面false所成角的正弦值为false.
20. 解:(Ⅰ)∵false,false,
∴当false时,false,∴false,
又false,∴false,
两式作商,有false,所以数列false隔项成以4为公比的等比数列.
∴false.
(Ⅱ)由已知数列false前false项和为false.
∴false,∴false.
两式相减得,false,∴false,
∴false.
21.(Ⅰ)解:false,可设椭圆方程为false,直线false的方程为:false,与椭圆联立方程可得:false.false①,
false,false,进一步计算可得:false.由false②.
当false时,由false,由false,所以false,
所以false;
当false时,①桓成立,由false,所以false.
(Ⅱ)解:false,结合false,false可解得:
false,false,
再将其代入false可得false.
falsefalse,
当false时,false,false有最大值;
当false,由(Ⅰ)知:由false,
(i)当false时,即false时,false无最大值;
(ii)当false时,即false,false有最大值.
综上当false时false有最大值,此时false,将false代入false,解得false,所以椭圆的方程为:false.
22. 解1:(分类讨论)
(Ⅰ)由题false,false是false的两个根,则false,同理false,则false,易知false,false,
展开化简得:false.
(Ⅱ)若存在false,使false,
因为false,false,
所以false,false,
当false时,false,false在false上单调递增,false,
所以false在false上单调递增,false,不满足题意.
当false时,则在false上false,在false上false,
所以false在false上单调递增,在false上单调递减,
又false,在false上false,从而false在false上单调递增,
又false,所以在false上false.
而当false时,false,
所以存在false,使false.
当false时,则false,false在false上单调递减,false,
所以false在false上单调递减,false,不满足题意.
综上所述:false.
解2:(参变量分离)
由题false有变号的零点,令false,false,
则false,令false,
则false.
则false在false上单调递增,false,故false.
则false在false上单调递增.
而false,
false.
1. 已知集合false,false,则( )
A. false B. false C. false D. false
2. 复数false(false为虚数单位)的共轭复数是( )
A. false B. false C. false D. false
3. 某几何体的三视图如图所示,则该几何体的体积是( )
A. false B. false C. false D. false
4. 函数false的图像可能是( )
A. B.
C. D.
5. 若实数false,false满足约束条件false,则false的取值范围是( )
A. false B. false C. false D. false
6. 小智参加三分投篮比赛,投中1次得1分,投不中扣1分,已知小智投篮命中率为0.5,记小智投篮三次后的得分为随机变量false,则false为( )
A. false B. false C. false D. 3
7. 已知数列false为等差数列,则“false为有理数”是“数列false中存在有理数” ( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
8. 已知平面向量false,false满足false,false,且false,则false的最小值是( )
A. false B. false C. false D. false
9. 如图,在false中,false,false,点false为线段false上一点,将false绕false翻折,若在翻折过程中存在某位置,使得false,记false为false的最小值.则( )
A. false B. false
C. false D. false
10. 记false(false为自然对数的底数),若对任意false,存在不等实数false,使得false,则满足条件的整数false的个数是( )
A. 2 B. 3 C. 4 D. 5
11. 早在两千多年前,我国的墨子给出了圆的定义“一中同长也”已知false为坐标原点,false,若false,false的“长”分别为1,false,且两圆相切,则false_________.
12. 二项式false的展开式中有_____________项有理项;这些项的系数之和是__________.
13. 在false中,角false,false,false所对的边分别为false,false,false,若false,false,false,则false_________;false的面积是__________.
14. 若定义在false上的偶函数满足false,false,则false___________﹔若实数false,false满足false,设函数false,则false在false上最少有____________个零点.
15. 已知椭圆false的左,右焦点分别为false,false,点false为直线false上的一个动点(不在坐标轴上),则当false的最大值为false时,椭圆的离心率是_________.
16. 如图,在false的点阵中,依次随机地选出false,false,false三个点,则选出的三点满足的概率是false的概率是___________;单调递增区间是__________.
18. 已知函数false.
(1)求函数false的振幅与单调区间;
(2)在false中,false为锐角,满足false,若false,求false.
19. 如图,已知四棱锥false中,false平面false,平面false平面false,且false,false,false,点false在平面false内的射影恰为false的重心false.
(1)证明:false;
(2)求直线false与平面false所成角的正弦值.
20. 已知数列false满足:false,false.
(Ⅰ)求数列false的通项公式;
(Ⅱ)若数列false满足数列false前false项和为false,求数列false的前false项和.
21. 已知椭圆false的离心率为false,过false作斜率为false的直线false交椭圆于false,false两点,false,false,false互不重合.
(Ⅰ)对于给定的false,若false,求false的取值范围(星空专用)(用false表示);
(Ⅱ)对于给定的false满足false(false且false),当false(false为坐标原点)的面积最大时,求椭圆的标准方程(用false表示).
22. 已知函数false,false.
(Ⅰ)若false,false是false的两个根,证明:false;
(Ⅱ)若存在false,使false,求false的取值范围.
2021年2月宁海中学创新班测试卷
1-5:DBADA 6-10:BABCD
11. 1 12. 3,225 13. 4,false 14. 所以至少2个零点
15. 设false到false轴的距离为false,
则falsefalse,解得:false.
16. 由题意可知false,false,false三个点是有序的,从反面false的角度做,讨论的是false为主元,
故对false分三种情况讨论,如图:第一类false为5号点;第二类false为1,3,7,9号点;
第三类false为2,4,6,8号点;
(1)当false为5号点时,则(i)false,三点共线有四条直线,故false,
(ii)false,则,如false在1号位,false和false即false,共有false,共有false种.
'
(2)当false为第二类点不存在这样的点;
(3)当false为第三类点,以2号点为例,有三种图示
故有false,综上false共有64中,故false.答案填:false.
18.(1)解:三角函数性质
因为false,
即false的振幅为2,∵false,∴false,
所以false的递增区间为false,递减区间为false.
(2)解:三角函数化简
∵false,∴false,
∴false或false,所以false或false,
∵false为锐角,∴false,∵false,∴false,∴false,
∴false,∴false,∴false,∴false,
∴false
false
false.
19. 解:(1)过false作false于false,因为平面false平面false,平面false平面false,false平面false,所以false平面false,∴false.因为false平面false,所以false,false,所以false平面false,∴false.
(2)连结false并延长交false于false,连结false.以false为原点,分别以false,false所在的直线为false,false轴,以过false且与平面false垂直的直线为false轴,建立空间直角坐标系,如图所示,则false,false,false,设false,∵false平面false,∴false,同理false,∴false,∴false平面false,∴false,∵false是false的重心,∴false是false的中点,∴false,由(1)知,false,∴false,∴false,false,∴false,∴false,∴false,设false,则false,故false,∴false,false,
∴false,∴false,∴false,∴false,false,false,设平面false的法向量为false,则false,false,令false,则false,设直线false与平面false所成角为false,则falsefalse,故直线false与平面false所成角的正弦值为false.
20. 解:(Ⅰ)∵false,false,
∴当false时,false,∴false,
又false,∴false,
两式作商,有false,所以数列false隔项成以4为公比的等比数列.
∴false.
(Ⅱ)由已知数列false前false项和为false.
∴false,∴false.
两式相减得,false,∴false,
∴false.
21.(Ⅰ)解:false,可设椭圆方程为false,直线false的方程为:false,与椭圆联立方程可得:false.false①,
false,false,进一步计算可得:false.由false②.
当false时,由false,由false,所以false,
所以false;
当false时,①桓成立,由false,所以false.
(Ⅱ)解:false,结合false,false可解得:
false,false,
再将其代入false可得false.
falsefalse,
当false时,false,false有最大值;
当false,由(Ⅰ)知:由false,
(i)当false时,即false时,false无最大值;
(ii)当false时,即false,false有最大值.
综上当false时false有最大值,此时false,将false代入false,解得false,所以椭圆的方程为:false.
22. 解1:(分类讨论)
(Ⅰ)由题false,false是false的两个根,则false,同理false,则false,易知false,false,
展开化简得:false.
(Ⅱ)若存在false,使false,
因为false,false,
所以false,false,
当false时,false,false在false上单调递增,false,
所以false在false上单调递增,false,不满足题意.
当false时,则在false上false,在false上false,
所以false在false上单调递增,在false上单调递减,
又false,在false上false,从而false在false上单调递增,
又false,所以在false上false.
而当false时,false,
所以存在false,使false.
当false时,则false,false在false上单调递减,false,
所以false在false上单调递减,false,不满足题意.
综上所述:false.
解2:(参变量分离)
由题false有变号的零点,令false,false,
则false,令false,
则false.
则false在false上单调递增,false,故false.
则false在false上单调递增.
而false,
false.
同课章节目录
