人教版初中数学九年级下册第二十七章相似单元测试题 (Word版含解析)
文档属性
| 名称 | 人教版初中数学九年级下册第二十七章相似单元测试题 (Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 170.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-02 07:36:27 | ||
图片预览




文档简介
人教版初中数学九年级下册
相似单元测试题
学校:__________
班级:__________
姓名:__________
考号:__________
?
1.
下列两个图形一定相似的是(?
?
?
?
)
A.两个菱形
B.两个矩形
C.两个正方形
D.两个等腰梯形
?
2.
若,相似比为,则与的面积比为(?
?
?
?
)
A.
B.
C.
D.
?
3.
下列各组图形中,不相似的是(
)
A.
B.
C.
D.
?
4.
下列每组的两个图形,是位似图形的是(?
?
?
?
)
A.
B.
C.
D.
?
5.
如图,与是位似图形,点为位似中心.已知,则与的面积比为(?
?
?
?
)
A.
B.
C.
D.
?
6.
下列各组图形中不一定相似的是?
?
?
?
A.两个矩形
B.两个正方形
C.各有一个角是的两个等腰三角形
D.两个等腰直角三角形
?
7.
如图,是的边上一点,那么下面四个命题中错误的是(
)
A.如果,则
B.如果,则
C.如果,则
D.如果,则
?
8.
在一张由复印机复印出来的纸上,一个多边形的一条边由原来的变成了,那么这个多边形的另一条边由原来变成了(
)
A.
B.
C.
D.
?
9.
如图,小明家客厅有一张直径为米,高米的圆桌,在距地面米的处有一盏灯,的影子为,依据题意建立平面直角坐标系,其中点的坐标为,则点的坐标为?
?
?
?
A.
B.
C.
D.
?
10.
如图,在中,,于,,,则为(
)
A.
B.
C.
D.
?
11.
已知与位似,与位似,则(
)
A.与全等
B.与位似
C.与相似但不一定位似
D.与不相似
?
12.
在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是(?
?
?
?
)
A.
B.
C.或
D.或
?
13.
下列说法中正确的是:所有的(
)都相似.
A.菱形
B.矩形
C.正方形
D.梯形
?
14.
如图,已知是线段上的任意一点(端点除外),分别以,为斜边并且在的同一侧作等腰直角和,连接交于点,连接交于点,给出以下三个结论:①;②;③,其中正确结论的个数是(
)
A.
B.
C.
D.
?
15.
如图,点在的边上,添加下列一个条件仍不能判断与相似的是(
)
A.
B.
C.·
D.·
?
16.
若,则等于(
)
A.或
B.
C.
D.不能确定
?
17.
小华同学自制了一个简易的幻灯机,其工作情况如图所示,幻灯片与屏幕平行,光源到幻灯片的距离是,幻灯片到屏幕的距离是,幻灯片上小树的高度是,则屏幕上小树的高度是?
?
?
?
A.
B.
C.
D.
?
18.
设想有一根铁丝套在地球的赤道上,刚好拉紧后,又放长了米,并使得铁丝均匀地离开地面.下面关于铁丝离开地面高度的说法中合理的是???(已知圆的周长公式,).
A.这个高度只能塞过一张纸
B.这个高度只能伸进你的拳头
C.这个高度只能钻过一只羊
D.这个高度能驶过一艘万吨巨轮
?
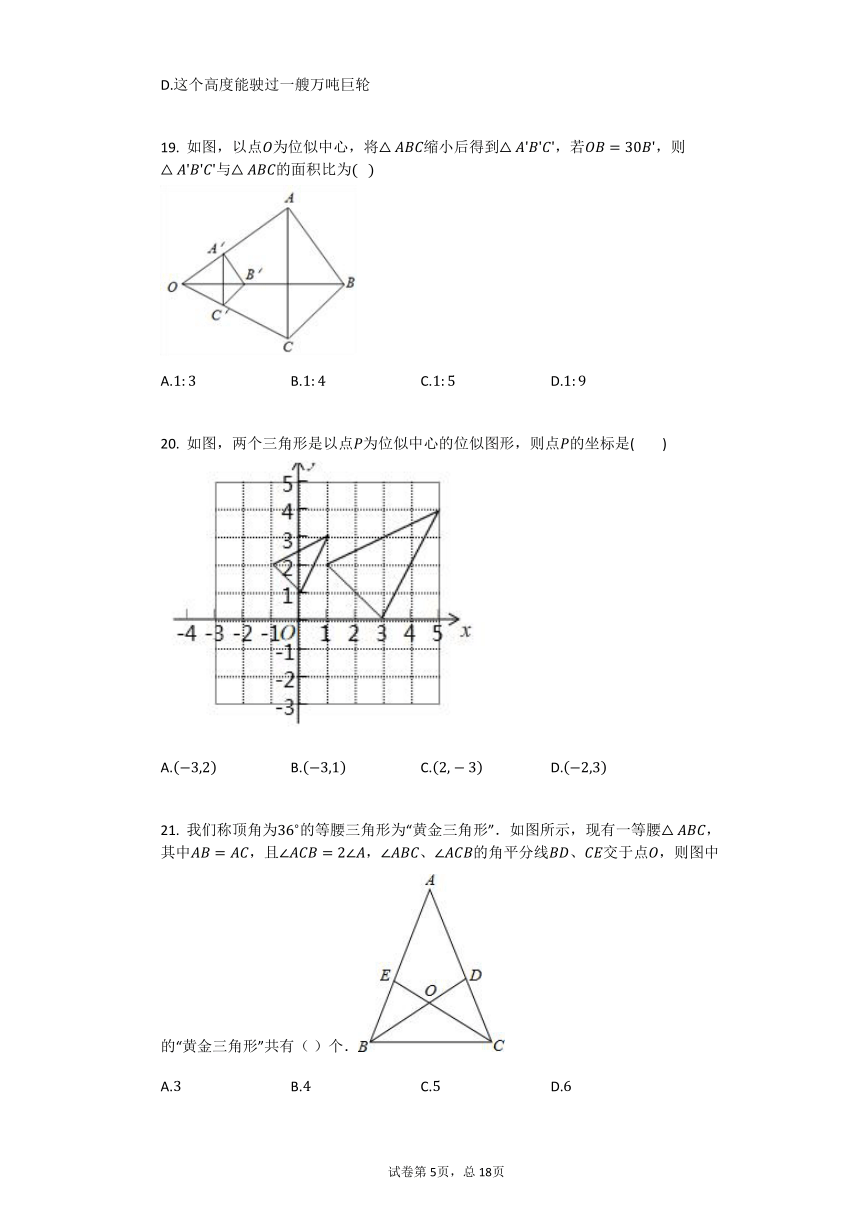
19.
如图,以点为位似中心,将缩小后得到,若,则与的面积比为???
A.
B.
C.
D.
?
20.
如图,两个三角形是以点为位似中心的位似图形,则点的坐标是(?
?
?
?
)
A.
B.
C.
D.
?
21.
我们称顶角为的等腰三角形为“黄金三角形”.如图所示,现有一等腰,其中,且,、的角平分线、交于点,则图中的“黄金三角形”共有(
)个.
A.
B.
C.
D.
?
22.
等腰三角形和相似,其相似比为,则它们底边上对应高线的比为(
)
A.
B.
C.
D.
?
23.
已知,,三个数,请你再添一个数使之成为比例式,写出这个比例式,如:________.
?
24.
将一个四边形各边都扩大倍,这个四边形的形状________.(填“改变了”或“没有改变”)
?
25.
勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.如图,线段,点是线段的黄金分割点,点是线段的黄金分割点,点是线段的黄金分割点,…,依此类推,则的长度是________.
?
26.
已知:如图,在中,,是上的中点,过点作,垂足为.
求证:.
?
27.
如图,是的中线,是上一点.且,连接交于点.求证:.
参考答案与试题解析
一、
选择题
(本题共计
22
小题
,每题
3
分
,共计66分
)
1.
【答案】
C
【考点】
相似图形
【解析】
根据相似图形的定义:对应角相等,对应边成比例的两个图形一定相似,结合选项,用排除法求解.
【解答】
解:,两个菱形,对应边成比例,对应角不一定相等,不符合相似的定义,故不符合题意;
,两个矩形,对应角相等,对应边不一定成比例,不符合相似的定义,故不符合题意;
,两个正方形,对应角相等,对应边一定成比例,一定相似,故符合题意;
,两个等腰梯形对应角不一定相等,对应边不一定成比例,不符合相似的定义,故不符合题意.
故选.
2.
【答案】
A
【考点】
相似三角形的性质
【解析】
根据相似三角形的面积的比等于相似比的平方解答即可.
【解答】
解:∵
,相似比为,
∴
根据相似三角形的面积的比等于相似比的平方,
即与的面积比为.
故选.
3.
【答案】
C
【考点】
相似图形
【解析】
根据相似图形的定义,结合图形,以选项一一分析,排除错误答案.
【解答】
解:、形状相同,但大小不同,符合相似定义,故此选项不合题意;
、形状相同,但大小不同,符合相似定义,故此选项不合题意;
、形状不同,不符合相似定义,故此选项符合题意;
、形状相同,但大小不同,符合相似定义,故此选项不合题意.
故选:.
4.
【答案】
D
【考点】
位似图形的判断
【解析】
此题暂无解析
【解答】
解:根据对应顶点的连线相交于一点的两个相似多边形叫位似图形可知,
只有选项符合题意.
故选.
5.
【答案】
D
【考点】
位似的性质
【解析】
根据题意可得两个三角形的相似比,从而求出面积比.
【解答】
解:因为与位似,,
所以与的相似比为,
所以与的面积比为.
故选.
6.
【答案】
A
【考点】
相似三角形的判定
相似图形
【解析】
根据相似图形的定义,结合图形,对选项——分析,利用排除法求解.
【解答】
解:两个矩形,对应角相等,但边的比不一定相等,故不一定相似,符合题意;
两个正方形,对应角相等,对应边成比例,故相似,不符合题意;
一定是等腰三角形的顶角,则顶角相等,两个底角也相等,则相似,不符合题意;
两个等腰直角三角形,都有一个直角和的锐角,故相似,不符合题意.
故选.
7.
【答案】
D
【考点】
相似三角形的判定
【解析】
相似三角形的判定,即对应角相等,对应边成比例.
【解答】
解:中,为公共角,所以正确;
中,为公共角,所以也正确;
中对应边成比例,对应角相等,也正确;
中对应边成比例,但夹角不相等,所以错误
故选
8.
【答案】
C
【考点】
相似多边形的性质
【解析】
复印机复印出来的两个多边形一定相似,依据相似多边形的对应边的比相等即可求解.
【解答】
解:设这个多边形的另一条边由原来变成了.
根据题意得:
解得:
故选.
9.
【答案】
C
【考点】
相似三角形的性质与判定
【解析】
根据相似三角形的判定和性质即可得到结论.
【解答】
解:∵
,
∴
,
∴
.
∵
,
∴
,
∴
.
故选.
10.
【答案】
B
【考点】
射影定理
【解析】
根据射影定理:直角三角形中,一条直角边是这条直角边在斜边上的射影与斜边的比例中项计算即可.
【解答】
解:由射影定理得,
,
∴
.
故选:.
11.
【答案】
C
【考点】
位似变换
【解析】
与位似,与位似,位似是特殊的相似,位似的两个图形一定形状相同,因而与相似,而与的位似中心与,与的位似不一定是同一个点,因而与相似但不一定位似.
【解答】
解:∵
与位似,与位似
∴
与相似;与相似但不一定位似.
故选.
12.
【答案】
A
【考点】
位似的有关计算
【解析】
此题暂无解析
【解答】
此题暂无解答
13.
【答案】
C
【考点】
相似图形
【解析】
根据相似图形的判定对各选项逐一分析,即可解答.
【解答】
解:、所有的菱形对应边之比都相等,但对应角不一定相等,故本选项错误;
、所有的矩形对应角都相等,但对应边不一定成比例,故本选项错误;
、所有的正方形对应边之比都相等,但对应角一定相等,故本选项正确;
、所有的梯形对应边之比不一定相等,对应角不一定相等,故本选项错误;
故选.
14.
【答案】
D
【考点】
相似三角形的性质与判定
平行线分线段成比例
【解析】
用平行线分线段成比例定理;
根据相似三角形的性质,化简分式可得;
要利用二次函数最值即可求解.
【解答】
解:∵
,
∴
,∴
①,
∵
,
∴
,∴
②,
∵
等腰直角和,
∴
,,
∴
,
∴
;
∵
,
∴
,
∴
,
设,
则,,
∵
,
∴
,
,
∴
,
∴
;
∵
,
∴
,
设(常数),,
则.
∴
正确的结论有个,
故选.
15.
【答案】
D
【考点】
相似三角形的性质与判定
【解析】
根据三角形相似的判定定理,分别判断得到答案即可.
【解答】
解:根据题意可知,
∴
当时,
当时,
当时,
当时,不能判定
故答案为:.
16.
【答案】
A
【考点】
比例的性质
【解析】
分两种情况讨论:当时和当=时.
【解答】
∵
,
∴
当时,;
当=时,,
17.
【答案】
C
【考点】
相似三角形的应用
【解析】
幻灯片上的像与在屏幕上的像是位似图形,位似比是;则小树的高度的比等于位似比.
【解答】
解:,.
设屏幕上小树的高度是米,则;
∴
.
故选.
18.
【答案】
C
【考点】
圆的有关概念
圆与四边形的综合
圆与相似的综合
【解析】
设地球半径是,铁丝均匀地离开地面的高度是
米.
故选:
【解答】
此题暂无解答
19.
【答案】
D
【考点】
位似变换
作图-位似变换
位似的性质
【解析】
由位似比可得出相似比,再根据相似三角形的性质:相似三角形的面积比等于相似比的平方即可求解.解:
以点为位似中心,将缩小后得到
故选
【解答】
此题暂无解答
20.
【答案】
A
【考点】
位似的有关计算
确定位似中心
【解析】
根据位似变换的概念找出位似中心,根据相似三角形的性质列出比例式,计算即可.
【解答】
解:如图点为位似中心,
∴
,
即,
解得,
∴
点的坐标为.
故选.
21.
【答案】
C
【考点】
黄金分割
【解析】
由在中,,,角平分线与相交于点,利用等边对等角与角平分线的性质,易求得图中各角的度数,然后利用“黄金三角形”的定义,即可判定,,,,都是“黄金三角形”.
【解答】
解:∵
在中,,,
∴
,
∵
的角平分线与相交于点,
∴
,,
∴
,
∴
,,
∴
,
∴
,,
∴
“黄金三角形”有:,,,,共个.
故选.
22.
【答案】
A
【考点】
相似三角形的性质
【解析】
直接根据相似三角形的性质进行解答即可.
【解答】
解:∵
等腰和相似,其相似比为,
∴
它们底边上对应高线的比等于.
故选.
二、
填空题
(本题共计
3
小题
,每题
3
分
,共计9分
)
23.
【答案】
【考点】
比例线段
【解析】
可以设再添上的数是,根据比例的定义就可解得.答案不唯一.
【解答】
解:设添上的数是,得到:,解得,则比例式是:.
故答案是::.
24.
【答案】
没有改变
【考点】
相似图形
【解析】
根据题意可知,扩大后的图形与原图形形状相同,大小不同,根据相似图形的定义直接得出结果.
【解答】
解:∵
相似图形的形状相同,但大小不一定相同,
∴
将一个四边形各边都扩大倍,这个四边形的形状没有改变.
25.
【答案】
【考点】
黄金分割
规律型:数字的变化类
【解析】
根据黄金分割的定义得到,则,同理得到,,根据此规律得到.
【解答】
解:∵
线段,点是线段的黄金分割点,
∴
,
∴
.
∵
点是线段的黄金分割点,
∴
,
∴
,
∴
.
故答案为:.
三、
解答题
(本题共计
2
小题
,每题
10
分
,共计20分
)
26.
【答案】
证明:∵
在中,,是上的中点,
∴
,,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
.
【考点】
相似三角形的判定
【解析】
利用直角三角形中斜边上的中线是斜边的一半可得三角形是等腰三角形,所以可得,再有一对直角相等即可证明.
【解答】
证明:∵
在中,,是上的中点,
∴
,,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
.
27.
【答案】
证明:过点作,交于,作,交于点,
∵
,,
∴
四边形是平行四边形,
∴
,,
∵
是的中线,
∴
,,
∵
,为中点,
∴
,
∵
,
∴
,
∴
为中点,
∴
是的中位线,
∴
,
∵
,
∴
,
在和中,
∴
,
∴
,
∴
.
【考点】
平行线分线段成比例
【解析】
首先过点作,交于,作,交于点,再根据平行线分线段成比例定理可得,然后证明可得,进而得到.
【解答】
证明:过点作,交于,作,交于点,
∵
,,
∴
四边形是平行四边形,
∴
,,
∵
是的中线,
∴
,,
∵
,为中点,
∴
,
∵
,
∴
,
∴
为中点,
∴
是的中位线,
∴
,
∵
,
∴
,
在和中,
∴
,
∴
,
∴
.
试卷第6页,总18页
试卷第9页,总18页
相似单元测试题
学校:__________
班级:__________
姓名:__________
考号:__________
?
1.
下列两个图形一定相似的是(?
?
?
?
)
A.两个菱形
B.两个矩形
C.两个正方形
D.两个等腰梯形
?
2.
若,相似比为,则与的面积比为(?
?
?
?
)
A.
B.
C.
D.
?
3.
下列各组图形中,不相似的是(
)
A.
B.
C.
D.
?
4.
下列每组的两个图形,是位似图形的是(?
?
?
?
)
A.
B.
C.
D.
?
5.
如图,与是位似图形,点为位似中心.已知,则与的面积比为(?
?
?
?
)
A.
B.
C.
D.
?
6.
下列各组图形中不一定相似的是?
?
?
?
A.两个矩形
B.两个正方形
C.各有一个角是的两个等腰三角形
D.两个等腰直角三角形
?
7.
如图,是的边上一点,那么下面四个命题中错误的是(
)
A.如果,则
B.如果,则
C.如果,则
D.如果,则
?
8.
在一张由复印机复印出来的纸上,一个多边形的一条边由原来的变成了,那么这个多边形的另一条边由原来变成了(
)
A.
B.
C.
D.
?
9.
如图,小明家客厅有一张直径为米,高米的圆桌,在距地面米的处有一盏灯,的影子为,依据题意建立平面直角坐标系,其中点的坐标为,则点的坐标为?
?
?
?
A.
B.
C.
D.
?
10.
如图,在中,,于,,,则为(
)
A.
B.
C.
D.
?
11.
已知与位似,与位似,则(
)
A.与全等
B.与位似
C.与相似但不一定位似
D.与不相似
?
12.
在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是(?
?
?
?
)
A.
B.
C.或
D.或
?
13.
下列说法中正确的是:所有的(
)都相似.
A.菱形
B.矩形
C.正方形
D.梯形
?
14.
如图,已知是线段上的任意一点(端点除外),分别以,为斜边并且在的同一侧作等腰直角和,连接交于点,连接交于点,给出以下三个结论:①;②;③,其中正确结论的个数是(
)
A.
B.
C.
D.
?
15.
如图,点在的边上,添加下列一个条件仍不能判断与相似的是(
)
A.
B.
C.·
D.·
?
16.
若,则等于(
)
A.或
B.
C.
D.不能确定
?
17.
小华同学自制了一个简易的幻灯机,其工作情况如图所示,幻灯片与屏幕平行,光源到幻灯片的距离是,幻灯片到屏幕的距离是,幻灯片上小树的高度是,则屏幕上小树的高度是?
?
?
?
A.
B.
C.
D.
?
18.
设想有一根铁丝套在地球的赤道上,刚好拉紧后,又放长了米,并使得铁丝均匀地离开地面.下面关于铁丝离开地面高度的说法中合理的是???(已知圆的周长公式,).
A.这个高度只能塞过一张纸
B.这个高度只能伸进你的拳头
C.这个高度只能钻过一只羊
D.这个高度能驶过一艘万吨巨轮
?
19.
如图,以点为位似中心,将缩小后得到,若,则与的面积比为???
A.
B.
C.
D.
?
20.
如图,两个三角形是以点为位似中心的位似图形,则点的坐标是(?
?
?
?
)
A.
B.
C.
D.
?
21.
我们称顶角为的等腰三角形为“黄金三角形”.如图所示,现有一等腰,其中,且,、的角平分线、交于点,则图中的“黄金三角形”共有(
)个.
A.
B.
C.
D.
?
22.
等腰三角形和相似,其相似比为,则它们底边上对应高线的比为(
)
A.
B.
C.
D.
?
23.
已知,,三个数,请你再添一个数使之成为比例式,写出这个比例式,如:________.
?
24.
将一个四边形各边都扩大倍,这个四边形的形状________.(填“改变了”或“没有改变”)
?
25.
勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉.生活中到处可见黄金分割的美.如图,线段,点是线段的黄金分割点,点是线段的黄金分割点,点是线段的黄金分割点,…,依此类推,则的长度是________.
?
26.
已知:如图,在中,,是上的中点,过点作,垂足为.
求证:.
?
27.
如图,是的中线,是上一点.且,连接交于点.求证:.
参考答案与试题解析
一、
选择题
(本题共计
22
小题
,每题
3
分
,共计66分
)
1.
【答案】
C
【考点】
相似图形
【解析】
根据相似图形的定义:对应角相等,对应边成比例的两个图形一定相似,结合选项,用排除法求解.
【解答】
解:,两个菱形,对应边成比例,对应角不一定相等,不符合相似的定义,故不符合题意;
,两个矩形,对应角相等,对应边不一定成比例,不符合相似的定义,故不符合题意;
,两个正方形,对应角相等,对应边一定成比例,一定相似,故符合题意;
,两个等腰梯形对应角不一定相等,对应边不一定成比例,不符合相似的定义,故不符合题意.
故选.
2.
【答案】
A
【考点】
相似三角形的性质
【解析】
根据相似三角形的面积的比等于相似比的平方解答即可.
【解答】
解:∵
,相似比为,
∴
根据相似三角形的面积的比等于相似比的平方,
即与的面积比为.
故选.
3.
【答案】
C
【考点】
相似图形
【解析】
根据相似图形的定义,结合图形,以选项一一分析,排除错误答案.
【解答】
解:、形状相同,但大小不同,符合相似定义,故此选项不合题意;
、形状相同,但大小不同,符合相似定义,故此选项不合题意;
、形状不同,不符合相似定义,故此选项符合题意;
、形状相同,但大小不同,符合相似定义,故此选项不合题意.
故选:.
4.
【答案】
D
【考点】
位似图形的判断
【解析】
此题暂无解析
【解答】
解:根据对应顶点的连线相交于一点的两个相似多边形叫位似图形可知,
只有选项符合题意.
故选.
5.
【答案】
D
【考点】
位似的性质
【解析】
根据题意可得两个三角形的相似比,从而求出面积比.
【解答】
解:因为与位似,,
所以与的相似比为,
所以与的面积比为.
故选.
6.
【答案】
A
【考点】
相似三角形的判定
相似图形
【解析】
根据相似图形的定义,结合图形,对选项——分析,利用排除法求解.
【解答】
解:两个矩形,对应角相等,但边的比不一定相等,故不一定相似,符合题意;
两个正方形,对应角相等,对应边成比例,故相似,不符合题意;
一定是等腰三角形的顶角,则顶角相等,两个底角也相等,则相似,不符合题意;
两个等腰直角三角形,都有一个直角和的锐角,故相似,不符合题意.
故选.
7.
【答案】
D
【考点】
相似三角形的判定
【解析】
相似三角形的判定,即对应角相等,对应边成比例.
【解答】
解:中,为公共角,所以正确;
中,为公共角,所以也正确;
中对应边成比例,对应角相等,也正确;
中对应边成比例,但夹角不相等,所以错误
故选
8.
【答案】
C
【考点】
相似多边形的性质
【解析】
复印机复印出来的两个多边形一定相似,依据相似多边形的对应边的比相等即可求解.
【解答】
解:设这个多边形的另一条边由原来变成了.
根据题意得:
解得:
故选.
9.
【答案】
C
【考点】
相似三角形的性质与判定
【解析】
根据相似三角形的判定和性质即可得到结论.
【解答】
解:∵
,
∴
,
∴
.
∵
,
∴
,
∴
.
故选.
10.
【答案】
B
【考点】
射影定理
【解析】
根据射影定理:直角三角形中,一条直角边是这条直角边在斜边上的射影与斜边的比例中项计算即可.
【解答】
解:由射影定理得,
,
∴
.
故选:.
11.
【答案】
C
【考点】
位似变换
【解析】
与位似,与位似,位似是特殊的相似,位似的两个图形一定形状相同,因而与相似,而与的位似中心与,与的位似不一定是同一个点,因而与相似但不一定位似.
【解答】
解:∵
与位似,与位似
∴
与相似;与相似但不一定位似.
故选.
12.
【答案】
A
【考点】
位似的有关计算
【解析】
此题暂无解析
【解答】
此题暂无解答
13.
【答案】
C
【考点】
相似图形
【解析】
根据相似图形的判定对各选项逐一分析,即可解答.
【解答】
解:、所有的菱形对应边之比都相等,但对应角不一定相等,故本选项错误;
、所有的矩形对应角都相等,但对应边不一定成比例,故本选项错误;
、所有的正方形对应边之比都相等,但对应角一定相等,故本选项正确;
、所有的梯形对应边之比不一定相等,对应角不一定相等,故本选项错误;
故选.
14.
【答案】
D
【考点】
相似三角形的性质与判定
平行线分线段成比例
【解析】
用平行线分线段成比例定理;
根据相似三角形的性质,化简分式可得;
要利用二次函数最值即可求解.
【解答】
解:∵
,
∴
,∴
①,
∵
,
∴
,∴
②,
∵
等腰直角和,
∴
,,
∴
,
∴
;
∵
,
∴
,
∴
,
设,
则,,
∵
,
∴
,
,
∴
,
∴
;
∵
,
∴
,
设(常数),,
则.
∴
正确的结论有个,
故选.
15.
【答案】
D
【考点】
相似三角形的性质与判定
【解析】
根据三角形相似的判定定理,分别判断得到答案即可.
【解答】
解:根据题意可知,
∴
当时,
当时,
当时,
当时,不能判定
故答案为:.
16.
【答案】
A
【考点】
比例的性质
【解析】
分两种情况讨论:当时和当=时.
【解答】
∵
,
∴
当时,;
当=时,,
17.
【答案】
C
【考点】
相似三角形的应用
【解析】
幻灯片上的像与在屏幕上的像是位似图形,位似比是;则小树的高度的比等于位似比.
【解答】
解:,.
设屏幕上小树的高度是米,则;
∴
.
故选.
18.
【答案】
C
【考点】
圆的有关概念
圆与四边形的综合
圆与相似的综合
【解析】
设地球半径是,铁丝均匀地离开地面的高度是
米.
故选:
【解答】
此题暂无解答
19.
【答案】
D
【考点】
位似变换
作图-位似变换
位似的性质
【解析】
由位似比可得出相似比,再根据相似三角形的性质:相似三角形的面积比等于相似比的平方即可求解.解:
以点为位似中心,将缩小后得到
故选
【解答】
此题暂无解答
20.
【答案】
A
【考点】
位似的有关计算
确定位似中心
【解析】
根据位似变换的概念找出位似中心,根据相似三角形的性质列出比例式,计算即可.
【解答】
解:如图点为位似中心,
∴
,
即,
解得,
∴
点的坐标为.
故选.
21.
【答案】
C
【考点】
黄金分割
【解析】
由在中,,,角平分线与相交于点,利用等边对等角与角平分线的性质,易求得图中各角的度数,然后利用“黄金三角形”的定义,即可判定,,,,都是“黄金三角形”.
【解答】
解:∵
在中,,,
∴
,
∵
的角平分线与相交于点,
∴
,,
∴
,
∴
,,
∴
,
∴
,,
∴
“黄金三角形”有:,,,,共个.
故选.
22.
【答案】
A
【考点】
相似三角形的性质
【解析】
直接根据相似三角形的性质进行解答即可.
【解答】
解:∵
等腰和相似,其相似比为,
∴
它们底边上对应高线的比等于.
故选.
二、
填空题
(本题共计
3
小题
,每题
3
分
,共计9分
)
23.
【答案】
【考点】
比例线段
【解析】
可以设再添上的数是,根据比例的定义就可解得.答案不唯一.
【解答】
解:设添上的数是,得到:,解得,则比例式是:.
故答案是::.
24.
【答案】
没有改变
【考点】
相似图形
【解析】
根据题意可知,扩大后的图形与原图形形状相同,大小不同,根据相似图形的定义直接得出结果.
【解答】
解:∵
相似图形的形状相同,但大小不一定相同,
∴
将一个四边形各边都扩大倍,这个四边形的形状没有改变.
25.
【答案】
【考点】
黄金分割
规律型:数字的变化类
【解析】
根据黄金分割的定义得到,则,同理得到,,根据此规律得到.
【解答】
解:∵
线段,点是线段的黄金分割点,
∴
,
∴
.
∵
点是线段的黄金分割点,
∴
,
∴
,
∴
.
故答案为:.
三、
解答题
(本题共计
2
小题
,每题
10
分
,共计20分
)
26.
【答案】
证明:∵
在中,,是上的中点,
∴
,,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
.
【考点】
相似三角形的判定
【解析】
利用直角三角形中斜边上的中线是斜边的一半可得三角形是等腰三角形,所以可得,再有一对直角相等即可证明.
【解答】
证明:∵
在中,,是上的中点,
∴
,,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
.
27.
【答案】
证明:过点作,交于,作,交于点,
∵
,,
∴
四边形是平行四边形,
∴
,,
∵
是的中线,
∴
,,
∵
,为中点,
∴
,
∵
,
∴
,
∴
为中点,
∴
是的中位线,
∴
,
∵
,
∴
,
在和中,
∴
,
∴
,
∴
.
【考点】
平行线分线段成比例
【解析】
首先过点作,交于,作,交于点,再根据平行线分线段成比例定理可得,然后证明可得,进而得到.
【解答】
证明:过点作,交于,作,交于点,
∵
,,
∴
四边形是平行四边形,
∴
,,
∵
是的中线,
∴
,,
∵
,为中点,
∴
,
∵
,
∴
,
∴
为中点,
∴
是的中位线,
∴
,
∵
,
∴
,
在和中,
∴
,
∴
,
∴
.
试卷第6页,总18页
试卷第9页,总18页
