5.1.2 导数的概念及其几何意义 课件-高中数学人教A版(2019)选择性必修第二册(20张PPT)
文档属性
| 名称 | 5.1.2 导数的概念及其几何意义 课件-高中数学人教A版(2019)选择性必修第二册(20张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览







文档简介
5.1.2导数的概念及其几何意义
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
前面我们研究了两类变化率问题:
一类是物理学中的问题,涉及平均速度和瞬时速度;
另一类是几何学中的问题,涉及割线斜率和切线斜率。
这两类问题来自不同的学科领域,但在解决问题时,都采用了由“平均变化率”逼近“瞬时变化率”的思想方法;问题的答案也有一样的表示形式.下面我们用上述思想方法研究更一般的问题.
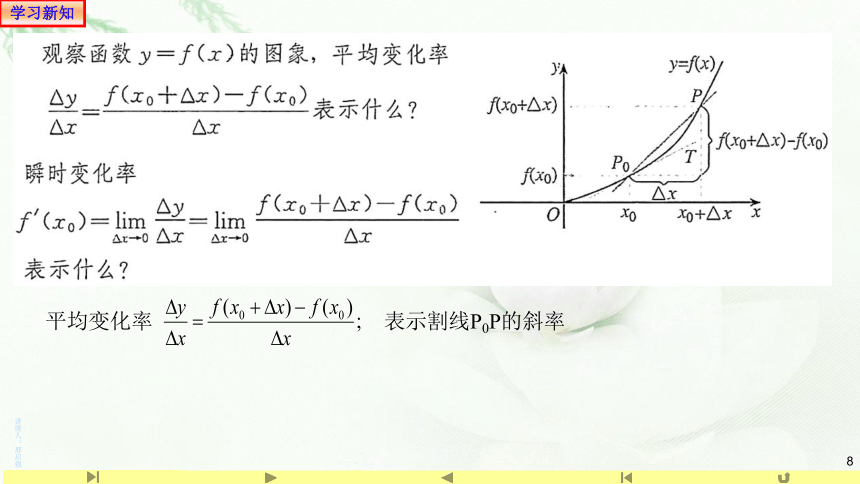
对于函数y=f(x),设自变量x从x0变化到x0+△x,相应地,函数值y就从f(x0)变化到f(x0+△x).
这时,x的变化量为△x,y的变化量为△y=f(x0+△x)-f(x0).我们把比值△????△y,即△????△?????=????(????0+△????)?????(????0)△????叫做函数y=f(x)从x0到x0+△x的平均变化率.
?
新知引入
定义:
函数 y = f (x) 在 x = x0 处的瞬时变化率是
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
学习新知
由导数的定义可知, 求函数 y = f (x)在x=x0处的导数的一般方法:
求函数的增量
2. 求平均变化率
3. 取极限得导数值
一差、二比、三极限
学习新知
例1:求函数y= 1????,在x=1处的导数.
?
练习:(1)求函数f(x)=-x2+x在x=-1附近的平均变化率,并求出在该点处的导数.
(2)质点运动规律为s=t2+3,求质点在t=3的瞬时速度.
3
6
典型例题
分析:先求Δf=Δy=f(1+Δx)-f(1) =6Δx+(Δx)2
典型例题
典型例题
例3一辆汽车在公路上沿直线变速行驶,假设ts时汽车的速度(单位:m/s)为
y=v(t)=-t2+6t+60,求汽车在第2s与第6s时的瞬时加速度,并说明它们的意义.
分析:瞬时加速度是速度关于时间的瞬时变化率,因此,在第2s与第6s时,汽车的瞬时加速度分别为v'(2),v'(6).
在第2s与第6s时,汽车的瞬时加速度分别是2m/s2与-6m/s2.
说明在第2s附近,汽车的速度每秒大约增加2m/s;
在第6s附近,汽车的速度每秒大约减少6m/s.
平均变化率 表示割线P0P的斜率
学习新知
P0
P
o
x
y
y=f(x)
割线
切线
T
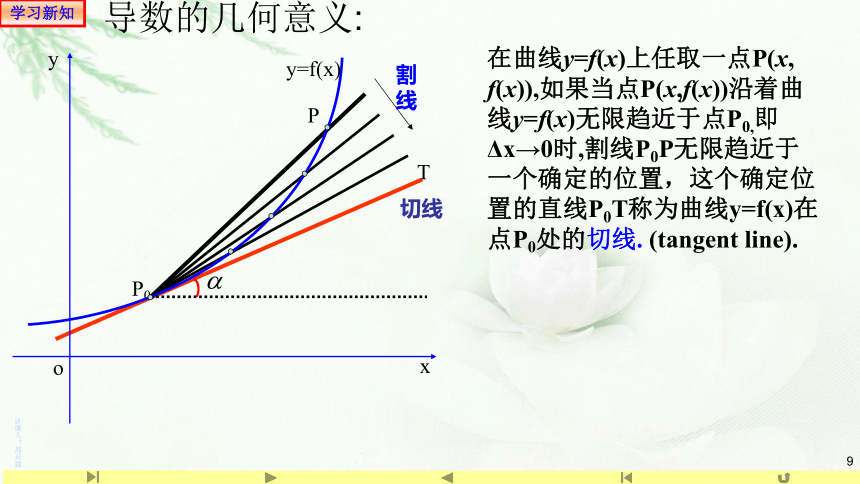
导数的几何意义:
在曲线y=f(x)上任取一点P(x, f(x)),如果当点P(x,f(x))沿着曲线y=f(x)无限趋近于点P0,即Δx→0时,割线P0P无限趋近于一个确定的位置,这个确定位置的直线P0T称为曲线y=f(x)在点P0处的切线. (tangent line).
学习新知
即:
这个几何意义: ①提供了求曲线上某点切线的斜率的一种方法;
②切线斜率的本质——函数在x=x0处的导数.
要注意,曲线在某点处的切线:
1)与该点的位置有关;
2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.
P0
P
o
x
y
y=f(x)
割线
切线
T
割线P0P的斜率k=?????????????????0?????????0. 记△x=x0-x,当点P沿着曲线y=f(x)无限趋近于点P0时,即当△x→0时,k无限趋近于函数y=f(x)在x=x0处的导数.
因此,函数y=f(x)在x=x0处的导数f '(x0)就是切线P0T的斜率k0.
?
这就是导数的几何意义
学习新知
解:我们用曲线h(t)在t=t0, t1,t2处的切线斜率,刻画曲线h(t)在上述三个时刻附近的变化情况.
(1)当t=t0时,曲线h(t)在t=t0处的切线l0平行于t轴,h'(t0)=0.这时,在t=t0附近曲线比较平坦,几乎没有升降.
(2)当t=t1时,曲线h(t)在t=t1处的切线l1的斜率h'(t1)<0.这时,在t=t1附近曲线下降,即函数h(t)在t=t1附近单调递减.
(3)当t=t2时,曲线h(t)在t=t2处的切线l2的斜率h’(t2)<0.这时,在t=t2附近曲线下降,即函数h(t)在t=t2附近也单调递减.
从图可以看出,直线l1的倾斜程度小于直线l2的倾斜程度,这说明曲线h(t)在t=t1附近比在t=t2附近下降得缓慢.
典型例题
由函数f(x)在x=x0处求导数的过程可以看到,当x=x0时,f '(x0) 是一个确定的数.
那么,当x变化时, f '(x)便是x的一个函数,我们叫它为f(x)的导函数(derived function)(简称导数), y=f(x)的导函数有时也记作y'即:
学习新知
例6:求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.
Q
P
y
=
x
2
+1
x
y
-
1
1
1
O
j
M
D
y
D
x
因此,切线方程为y-2=2(x-1),即y=2x.
求曲线在某点处的切线方程的基本步骤:
①求出P点的坐标;
②利用切线斜率的定义求出切线的斜率;
③利用点斜式求切线方程.
典型例题
练习:如图已知曲线 ,
求:(1)点P处的切线的斜率; (2)点P处的切线方程.
y
x
-2
-1
1
2
-2
-1
1
2
3
4
O
P
即点P处的切线的斜率等于4.
(2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
巩固练习
例7:在曲线y=x2上求分别满足下列条件的切线方程:
(1)平行于直线y=4x-5;
(2)垂直于直线2x-6y+5=0;(3)倾斜角为135°.
分析:解此类题的步骤为:
①先设切点坐标(x0,y0);
②求导函数f '(x);
③求切线的斜率f ' (x0);
④由斜率间的关系列出关于x0的方程,解方程求x0;
⑤由于点(x0,y0)在曲线y=f(x)上,将x0代入求y0,得切点坐标.
典型例题
例7:在曲线y=x2上求分别满足下列条件的切线方程,
(1)平行于直线y=4x-5;
(2)垂直于直线2x-6y+5=0;
(3)倾斜角为135°.
点评:此类题的易错之处是将切点的横坐标代入导函数来求切点坐标.
1求物体运动的瞬时速度:
(1)求位移增量Δs=s(t+Δt)-s(t)
(2)求平均速度
(3)求极限
2由导数的定义可得求导数的一般步骤:
(1)求函数的增量Δy=f(x0+Δt)-f(x0)
(2)求平均变化率
(3)求极限
课堂小结
O
A
B
x
y
Y=f(x)
x1
x2
f(x1)
f(x2)
x2-x1=△x
f(x2)-f(x1)=△y
前面我们研究了两类变化率问题:
一类是物理学中的问题,涉及平均速度和瞬时速度;
另一类是几何学中的问题,涉及割线斜率和切线斜率。
这两类问题来自不同的学科领域,但在解决问题时,都采用了由“平均变化率”逼近“瞬时变化率”的思想方法;问题的答案也有一样的表示形式.下面我们用上述思想方法研究更一般的问题.
对于函数y=f(x),设自变量x从x0变化到x0+△x,相应地,函数值y就从f(x0)变化到f(x0+△x).
这时,x的变化量为△x,y的变化量为△y=f(x0+△x)-f(x0).我们把比值△????△y,即△????△?????=????(????0+△????)?????(????0)△????叫做函数y=f(x)从x0到x0+△x的平均变化率.
?
新知引入
定义:
函数 y = f (x) 在 x = x0 处的瞬时变化率是
称为函数 y = f (x) 在 x = x0 处的导数, 记作
或 , 即
学习新知
由导数的定义可知, 求函数 y = f (x)在x=x0处的导数的一般方法:
求函数的增量
2. 求平均变化率
3. 取极限得导数值
一差、二比、三极限
学习新知
例1:求函数y= 1????,在x=1处的导数.
?
练习:(1)求函数f(x)=-x2+x在x=-1附近的平均变化率,并求出在该点处的导数.
(2)质点运动规律为s=t2+3,求质点在t=3的瞬时速度.
3
6
典型例题
分析:先求Δf=Δy=f(1+Δx)-f(1) =6Δx+(Δx)2
典型例题
典型例题
例3一辆汽车在公路上沿直线变速行驶,假设ts时汽车的速度(单位:m/s)为
y=v(t)=-t2+6t+60,求汽车在第2s与第6s时的瞬时加速度,并说明它们的意义.
分析:瞬时加速度是速度关于时间的瞬时变化率,因此,在第2s与第6s时,汽车的瞬时加速度分别为v'(2),v'(6).
在第2s与第6s时,汽车的瞬时加速度分别是2m/s2与-6m/s2.
说明在第2s附近,汽车的速度每秒大约增加2m/s;
在第6s附近,汽车的速度每秒大约减少6m/s.
平均变化率 表示割线P0P的斜率
学习新知
P0
P
o
x
y
y=f(x)
割线
切线
T
导数的几何意义:
在曲线y=f(x)上任取一点P(x, f(x)),如果当点P(x,f(x))沿着曲线y=f(x)无限趋近于点P0,即Δx→0时,割线P0P无限趋近于一个确定的位置,这个确定位置的直线P0T称为曲线y=f(x)在点P0处的切线. (tangent line).
学习新知
即:
这个几何意义: ①提供了求曲线上某点切线的斜率的一种方法;
②切线斜率的本质——函数在x=x0处的导数.
要注意,曲线在某点处的切线:
1)与该点的位置有关;
2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.
P0
P
o
x
y
y=f(x)
割线
切线
T
割线P0P的斜率k=?????????????????0?????????0. 记△x=x0-x,当点P沿着曲线y=f(x)无限趋近于点P0时,即当△x→0时,k无限趋近于函数y=f(x)在x=x0处的导数.
因此,函数y=f(x)在x=x0处的导数f '(x0)就是切线P0T的斜率k0.
?
这就是导数的几何意义
学习新知
解:我们用曲线h(t)在t=t0, t1,t2处的切线斜率,刻画曲线h(t)在上述三个时刻附近的变化情况.
(1)当t=t0时,曲线h(t)在t=t0处的切线l0平行于t轴,h'(t0)=0.这时,在t=t0附近曲线比较平坦,几乎没有升降.
(2)当t=t1时,曲线h(t)在t=t1处的切线l1的斜率h'(t1)<0.这时,在t=t1附近曲线下降,即函数h(t)在t=t1附近单调递减.
(3)当t=t2时,曲线h(t)在t=t2处的切线l2的斜率h’(t2)<0.这时,在t=t2附近曲线下降,即函数h(t)在t=t2附近也单调递减.
从图可以看出,直线l1的倾斜程度小于直线l2的倾斜程度,这说明曲线h(t)在t=t1附近比在t=t2附近下降得缓慢.
典型例题
由函数f(x)在x=x0处求导数的过程可以看到,当x=x0时,f '(x0) 是一个确定的数.
那么,当x变化时, f '(x)便是x的一个函数,我们叫它为f(x)的导函数(derived function)(简称导数), y=f(x)的导函数有时也记作y'即:
学习新知
例6:求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.
Q
P
y
=
x
2
+1
x
y
-
1
1
1
O
j
M
D
y
D
x
因此,切线方程为y-2=2(x-1),即y=2x.
求曲线在某点处的切线方程的基本步骤:
①求出P点的坐标;
②利用切线斜率的定义求出切线的斜率;
③利用点斜式求切线方程.
典型例题
练习:如图已知曲线 ,
求:(1)点P处的切线的斜率; (2)点P处的切线方程.
y
x
-2
-1
1
2
-2
-1
1
2
3
4
O
P
即点P处的切线的斜率等于4.
(2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.
巩固练习
例7:在曲线y=x2上求分别满足下列条件的切线方程:
(1)平行于直线y=4x-5;
(2)垂直于直线2x-6y+5=0;(3)倾斜角为135°.
分析:解此类题的步骤为:
①先设切点坐标(x0,y0);
②求导函数f '(x);
③求切线的斜率f ' (x0);
④由斜率间的关系列出关于x0的方程,解方程求x0;
⑤由于点(x0,y0)在曲线y=f(x)上,将x0代入求y0,得切点坐标.
典型例题
例7:在曲线y=x2上求分别满足下列条件的切线方程,
(1)平行于直线y=4x-5;
(2)垂直于直线2x-6y+5=0;
(3)倾斜角为135°.
点评:此类题的易错之处是将切点的横坐标代入导函数来求切点坐标.
1求物体运动的瞬时速度:
(1)求位移增量Δs=s(t+Δt)-s(t)
(2)求平均速度
(3)求极限
2由导数的定义可得求导数的一般步骤:
(1)求函数的增量Δy=f(x0+Δt)-f(x0)
(2)求平均变化率
(3)求极限
课堂小结
