3.3二元一次不等式组与简单的线性规划问题课件(苏教版必修5)
文档属性
| 名称 | 3.3二元一次不等式组与简单的线性规划问题课件(苏教版必修5) |  | |
| 格式 | rar | ||
| 文件大小 | 215.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-30 15:18:12 | ||
图片预览





文档简介
(共22张PPT)
第一节
二元一次不等式表示平面区域
问题1:在平面直坐标系中,
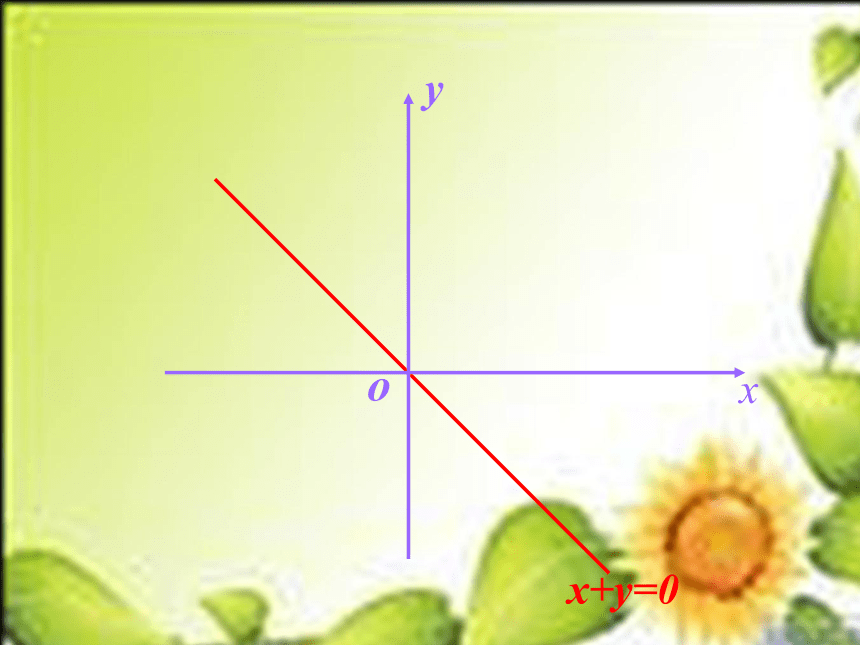
x+y=0
表示的点的集合表示什么图形?
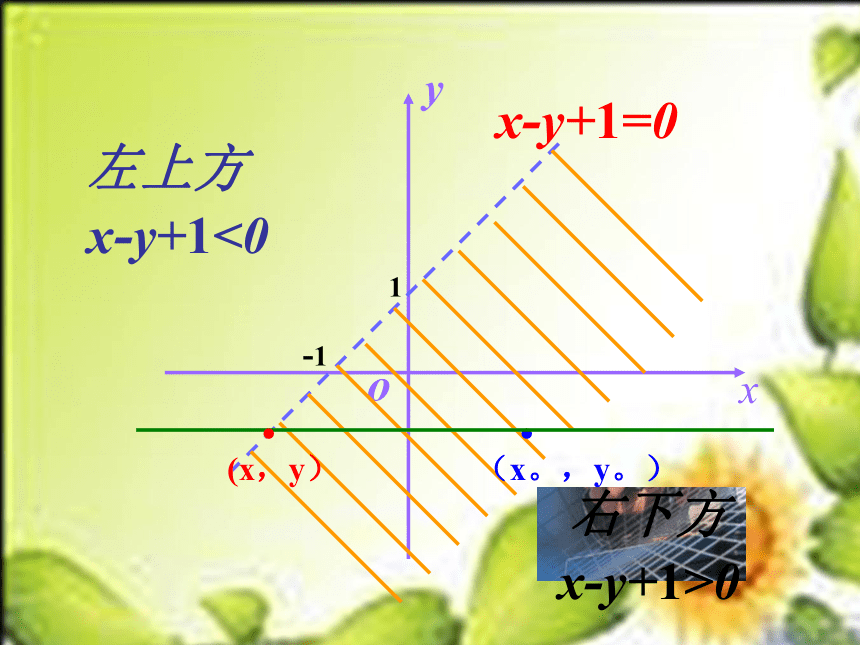
x-y+1>0 呢?
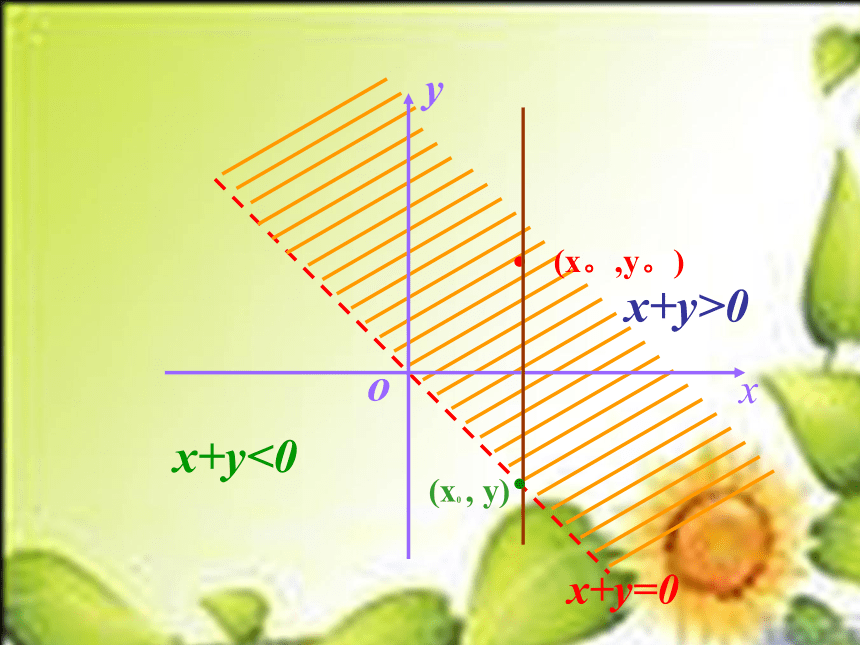
x+y>0 呢
x
y
o
x+y=0
x
y
o
x+y=0
x
y
o
x+y=0
x+y>0
x+y<0
(x。,y。)
(x0 , y)
在平面直角坐标系中, 点的集合{(x,y)|x-y+1=0}表示什么图形?
想一想?
x0>x,y=y0
x0-y0+1> x-y+1
x
y
o
1
-1
左上方
x-y+1<0
x-y+1=0
(x,y)
(x。,y。)
右下方
x-y+1>0
问题:一般地,如何画不等式AX+BY+C>0表示的平面区域?
(1)二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
(2)由于对直线同一侧的所有点(x,y),把它代入Ax+By+C,所得实数的符号都相同,所以只需在此直线的某一侧取一个特殊点(x0,y0) ,从Ax0+By0+C的正负可以判断出Ax+By+C>0表示哪一侧的区域。
一般在C≠0时,取原点作为特殊点。
例1:画出不等式
2x+y-6<0
表示的平面区域。
x
y
o
3
6
2x+y-6<0
2x+y-6=0
平面区域的确定常采用“直线定界,特殊点定域”的方法。
解:
将直线2X+y-6=0画成虚线
将(0,0)代入2X+y-6
得0+0-6=-6<0
原点所在一侧为
2x+y-6<0表示平面区域
练习1:
画出下列不等式表示的平面区域:
(1)2x+3y-6>0
(2)4x-3y≤12
O
X
Y
3
2
O
Y
X
3
-4
(1)
(2)
例2:画出不等式组
表示的平面区域
O
X
Y
x+y=0
x=3
x-y+5=0
注:不等式组表示的平面区域是各不等式
所表示平面区域的公共部分。
-5
5
解:
0-0+5>0
1+0>0
(1)
(2)
4
o
x
Y
-2
O
X
Y
3
3
2
练习2 :1.画出下列不等式组表示的平面区域
2
二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
确定步骤:
直线定界,特殊点定域;
若C≠0,则直线定界,原点定域;
小结:
(1)
例3:根据所给图形,把图中的平面区域用不等式表示出来:
(2)
应该注意的几个问题:
1、若不等式中不含0,则边界应画成虚线,
2、画图时应非常准确,否则将得不到正确结果。
3、熟记“直线定界、特殊点定域”方法的内涵。
否则应画成实线。
则用不等式可表示为:
解:此平面区域在x-y=0的右下方, x-y≥0
它又在x+2y-4=0的左下方, x+2y-4≤0
它还在y+2=0的上方, y+2≥0
Y
o
x
4
-2
x-y=0
y+2=0
x+2y-4=0
2
2,求由三直线x-y=0;x+2y-4=0及y+2=0
所围成的平面区域所表示的不等式。
一、引例:
某工厂生产甲、乙两种产品,生产1t甲两种产品需要A种原料4t、 B种原料12t,产生的利润为2万元;生产乙种产品需要A种原料1t、 B种原料9t,产生的利润为1万元。现有库存A种原料10t、 B种原料60t,如何安排生产才能使利润最大?
A种原料 B种原料 利润
甲种产品 4 12 2
乙种产品 1 9 1
现有库存 10 60
在关数据列表如下:
设生产甲、乙两种产品的吨数分别为x、y
利润
何时达到最大?
第一节
二元一次不等式表示平面区域
问题1:在平面直坐标系中,
x+y=0
表示的点的集合表示什么图形?
x-y+1>0 呢?
x+y>0 呢
x
y
o
x+y=0
x
y
o
x+y=0
x
y
o
x+y=0
x+y>0
x+y<0
(x。,y。)
(x0 , y)
在平面直角坐标系中, 点的集合{(x,y)|x-y+1=0}表示什么图形?
想一想?
x0>x,y=y0
x0-y0+1> x-y+1
x
y
o
1
-1
左上方
x-y+1<0
x-y+1=0
(x,y)
(x。,y。)
右下方
x-y+1>0
问题:一般地,如何画不等式AX+BY+C>0表示的平面区域?
(1)二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
(2)由于对直线同一侧的所有点(x,y),把它代入Ax+By+C,所得实数的符号都相同,所以只需在此直线的某一侧取一个特殊点(x0,y0) ,从Ax0+By0+C的正负可以判断出Ax+By+C>0表示哪一侧的区域。
一般在C≠0时,取原点作为特殊点。
例1:画出不等式
2x+y-6<0
表示的平面区域。
x
y
o
3
6
2x+y-6<0
2x+y-6=0
平面区域的确定常采用“直线定界,特殊点定域”的方法。
解:
将直线2X+y-6=0画成虚线
将(0,0)代入2X+y-6
得0+0-6=-6<0
原点所在一侧为
2x+y-6<0表示平面区域
练习1:
画出下列不等式表示的平面区域:
(1)2x+3y-6>0
(2)4x-3y≤12
O
X
Y
3
2
O
Y
X
3
-4
(1)
(2)
例2:画出不等式组
表示的平面区域
O
X
Y
x+y=0
x=3
x-y+5=0
注:不等式组表示的平面区域是各不等式
所表示平面区域的公共部分。
-5
5
解:
0-0+5>0
1+0>0
(1)
(2)
4
o
x
Y
-2
O
X
Y
3
3
2
练习2 :1.画出下列不等式组表示的平面区域
2
二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
确定步骤:
直线定界,特殊点定域;
若C≠0,则直线定界,原点定域;
小结:
(1)
例3:根据所给图形,把图中的平面区域用不等式表示出来:
(2)
应该注意的几个问题:
1、若不等式中不含0,则边界应画成虚线,
2、画图时应非常准确,否则将得不到正确结果。
3、熟记“直线定界、特殊点定域”方法的内涵。
否则应画成实线。
则用不等式可表示为:
解:此平面区域在x-y=0的右下方, x-y≥0
它又在x+2y-4=0的左下方, x+2y-4≤0
它还在y+2=0的上方, y+2≥0
Y
o
x
4
-2
x-y=0
y+2=0
x+2y-4=0
2
2,求由三直线x-y=0;x+2y-4=0及y+2=0
所围成的平面区域所表示的不等式。
一、引例:
某工厂生产甲、乙两种产品,生产1t甲两种产品需要A种原料4t、 B种原料12t,产生的利润为2万元;生产乙种产品需要A种原料1t、 B种原料9t,产生的利润为1万元。现有库存A种原料10t、 B种原料60t,如何安排生产才能使利润最大?
A种原料 B种原料 利润
甲种产品 4 12 2
乙种产品 1 9 1
现有库存 10 60
在关数据列表如下:
设生产甲、乙两种产品的吨数分别为x、y
利润
何时达到最大?
