6.4圆周运动的临界问题 课件 22张PPT
文档属性
| 名称 | 6.4圆周运动的临界问题 课件 22张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 675.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-02 15:30:40 | ||
图片预览







文档简介
6.4 圆周运动的临界问题
一、水平面内圆周运动的临界问题
(1)题型简述:
在水平面内做圆周运动的物体,当转速变化时,会出现绳子张紧(或恰好拉直)、绳子突然断裂、静摩擦力达最大值、弹簧弹力大小或方向发生变化等,从而出现临界问题。
(2)方法突破——步骤:
①判断临界状态:
有些题目中有“刚好”“恰好”“正好”等字眼,明显表明题述的过程存在着临界点;
若题目中有“取值范围”“多长时间”“多大距离”等词语,表明题述的过程存在着“起止点”,对应着临界状态;
若题目中有“最大”“最小”“至多”“至少”等字眼,表明题述的过程存在着极值,这个极值点也往往对应着临界状态。
(2)方法突破——步骤:
②确定临界条件:判断题述的过程存在临界状态之后,要通过分析弄清临界状态出现的条件,并以数学形式表达出来。
③选择物理规律:当确定了物体运动的临界状态和临界条件后,要分别对不同的运动过程或现象,选择相对应的物理规律,然后列方程求解。
(3)水平面内圆周运动临界问题的分析技巧
①在水平面内做圆周运动的物体,当角速度ω 变化时,物体有远离或向着圆心运动的趋势(半径有变化)。这时要根据物体的受力情况,判断某个力是否存在以及这个力存在时方向朝哪(特别是一些接触力,如静摩擦力、绳的拉力等)。
(3)水平面内圆周运动临界问题的分析技巧
②三种临界情况:
接触与脱离的临界条件:两物体相接触或脱离,临界条件是:弹力FN=0。
相对滑动的临界条件:两物体相接触且处于相对静止时,常存在着静摩擦力,则相对滑动的临界条件是:静摩擦力达到最大值。
绳子断裂与松驰(或恰好拉直)的临界条件:绳子所能承受的张力是有限度的,绳子断与不断的临界条件是绳中张力等于它所能承受的最大张力,绳子松弛(或恰好拉直)的临界条件是:FT=0。
(4)水平面内圆周运动的临界极值问题通常有两类:
一类是与摩擦力有关的临界问题;一类是与弹力有关的临界问题。
第一、与摩擦力有关的临界极值问题
物体间恰好不发生相对滑动 的临界条件是物体间恰好达到最大静摩擦力。
①如果只是摩擦力提供向心力,则有Fm= ,静摩擦力的方向一定指向圆心;
v2
r
m
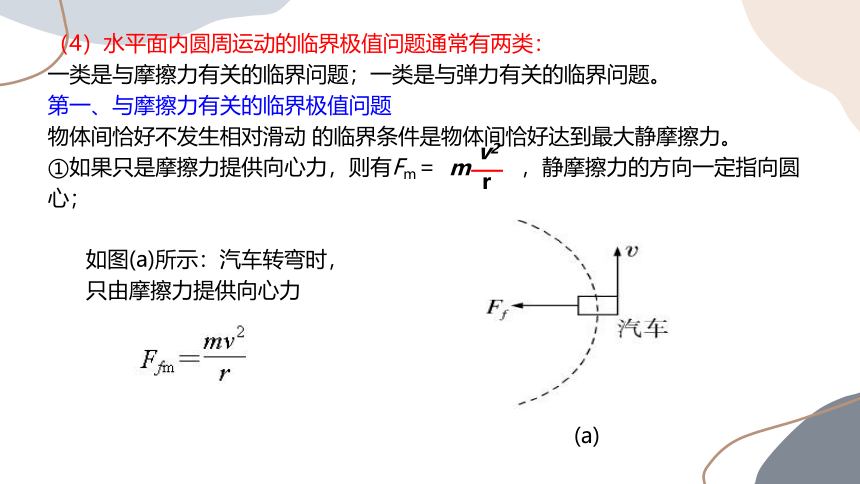
如图(a)所示:汽车转弯时,
只由摩擦力提供向心力
(a)
(b)
(c)
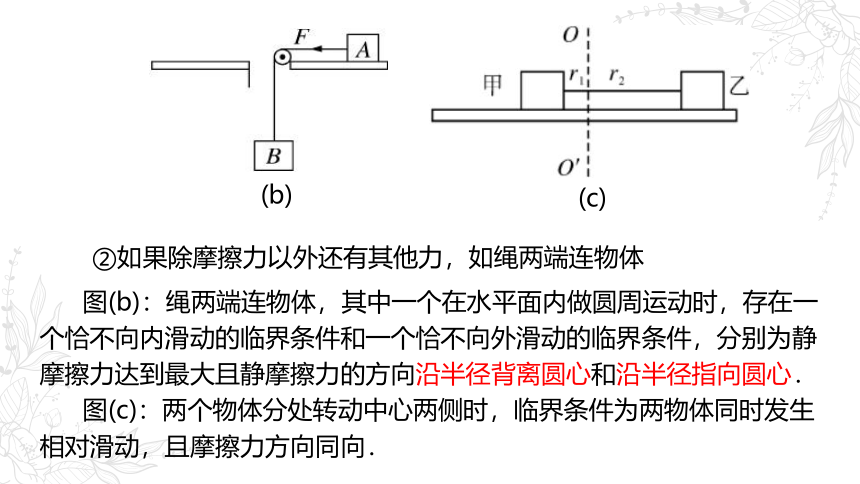
图(b):绳两端连物体,其中一个在水平面内做圆周运动时,存在一个恰不向内滑动的临界条件和一个恰不向外滑动的临界条件,分别为静摩擦力达到最大且静摩擦力的方向沿半径背离圆心和沿半径指向圆心.
图(c):两个物体分处转动中心两侧时,临界条件为两物体同时发生相对滑动,且摩擦力方向同向.
②如果除摩擦力以外还有其他力,如绳两端连物体
第二、与弹力有关的临界极值问题
①压力、支持力的临界条件是物体间的弹力恰好为零;
②绳上拉力的临界条件是绳恰好拉直且其上无弹力或绳上拉力恰好为最大承受力等。
【例1】如图所示,用一根长为 l=1 m的细线,一端系一质量为m=1 kg的小球(可视为质点), 另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT(sin37°=0.6,cos 37°=0.8,g取10 m/s2,结果可用根式表示)。求:
(1)若要小球离开锥面,则小球的角速度ω0至少为多大?
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大?
二、竖直面内圆周运动的临界问题
1、轻绳(或内轨道)——小球组成无支撑的物理模型(称为“轻绳模型”)
绳约束
内轨道约束
注:“轻绳”只能对小球产生拉力,不能产生支持力。(内轨道约束类似)
mg
O
绳
mg
O
轨道
小球恰好过最高点的条件:
当v=v0,小球恰好能够通过最高点;
当v当v>v0,小球能够通过最高点。
最高点:
小球在最低点时:
绳对小球产生竖直向上的拉力(若是内轨道则产生竖直向上的支持力)
v
o
mg
T1
最低点:
v2
mg
T2
L
故
(超重)
2、轻杆(或管道)——小球组成有支撑的物理模型(称为“轻杆模型”)
杆约束
管道约束
注:“轻杆”既能对小球产生拉力,也能产生支持力。(管道约束类似)
物理情景
图示
在最高点的临界特点
做圆周运动条件
细绳拉着小球在竖直平面内运动
T=0
在最高点时速度应不小于
小球在竖直放置的光滑圆环内侧运动
FN=0
在最高点时速度应不小于
小球固定在轻杆上在竖直面内运动
V>0
F向>0
F向=FT+mg 或F向=mg-Fn
在最高点速度应大于0
小球在竖直放置的光滑管中运动
V>0
F向>0
F向=FT+mg 或F向=mg-Fn
在最高点速度应大于0
绳子系着装有水的木桶,在竖直面内做圆周运动,水的质量m=0.5kg,绳子长度为L=60cm,求:
(1)最高点水不留出的最小速度?
(2)设水在最高点速度为v=3m/s,求水对桶底的压力?
(1)在最高点水不流出的最小速率为 m/s.
(2)水对桶底的压力为2.5N.
如图所示,一质量为m的小球,用长为L轻杆固定住,使其在竖直面内作圆周运动.(1)若小球恰好能通过最高点,则小球在最高点是多少?小球的受力情况如何?(2)若小球在最低点受到杆子的拉力为3mg,则小球在最低点的速度是多少?
O
(1)速度为0,受到重力和向上的支持力
(2)
一、水平面内圆周运动的临界问题
(1)题型简述:
在水平面内做圆周运动的物体,当转速变化时,会出现绳子张紧(或恰好拉直)、绳子突然断裂、静摩擦力达最大值、弹簧弹力大小或方向发生变化等,从而出现临界问题。
(2)方法突破——步骤:
①判断临界状态:
有些题目中有“刚好”“恰好”“正好”等字眼,明显表明题述的过程存在着临界点;
若题目中有“取值范围”“多长时间”“多大距离”等词语,表明题述的过程存在着“起止点”,对应着临界状态;
若题目中有“最大”“最小”“至多”“至少”等字眼,表明题述的过程存在着极值,这个极值点也往往对应着临界状态。
(2)方法突破——步骤:
②确定临界条件:判断题述的过程存在临界状态之后,要通过分析弄清临界状态出现的条件,并以数学形式表达出来。
③选择物理规律:当确定了物体运动的临界状态和临界条件后,要分别对不同的运动过程或现象,选择相对应的物理规律,然后列方程求解。
(3)水平面内圆周运动临界问题的分析技巧
①在水平面内做圆周运动的物体,当角速度ω 变化时,物体有远离或向着圆心运动的趋势(半径有变化)。这时要根据物体的受力情况,判断某个力是否存在以及这个力存在时方向朝哪(特别是一些接触力,如静摩擦力、绳的拉力等)。
(3)水平面内圆周运动临界问题的分析技巧
②三种临界情况:
接触与脱离的临界条件:两物体相接触或脱离,临界条件是:弹力FN=0。
相对滑动的临界条件:两物体相接触且处于相对静止时,常存在着静摩擦力,则相对滑动的临界条件是:静摩擦力达到最大值。
绳子断裂与松驰(或恰好拉直)的临界条件:绳子所能承受的张力是有限度的,绳子断与不断的临界条件是绳中张力等于它所能承受的最大张力,绳子松弛(或恰好拉直)的临界条件是:FT=0。
(4)水平面内圆周运动的临界极值问题通常有两类:
一类是与摩擦力有关的临界问题;一类是与弹力有关的临界问题。
第一、与摩擦力有关的临界极值问题
物体间恰好不发生相对滑动 的临界条件是物体间恰好达到最大静摩擦力。
①如果只是摩擦力提供向心力,则有Fm= ,静摩擦力的方向一定指向圆心;
v2
r
m
如图(a)所示:汽车转弯时,
只由摩擦力提供向心力
(a)
(b)
(c)
图(b):绳两端连物体,其中一个在水平面内做圆周运动时,存在一个恰不向内滑动的临界条件和一个恰不向外滑动的临界条件,分别为静摩擦力达到最大且静摩擦力的方向沿半径背离圆心和沿半径指向圆心.
图(c):两个物体分处转动中心两侧时,临界条件为两物体同时发生相对滑动,且摩擦力方向同向.
②如果除摩擦力以外还有其他力,如绳两端连物体
第二、与弹力有关的临界极值问题
①压力、支持力的临界条件是物体间的弹力恰好为零;
②绳上拉力的临界条件是绳恰好拉直且其上无弹力或绳上拉力恰好为最大承受力等。
【例1】如图所示,用一根长为 l=1 m的细线,一端系一质量为m=1 kg的小球(可视为质点), 另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT(sin37°=0.6,cos 37°=0.8,g取10 m/s2,结果可用根式表示)。求:
(1)若要小球离开锥面,则小球的角速度ω0至少为多大?
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大?
二、竖直面内圆周运动的临界问题
1、轻绳(或内轨道)——小球组成无支撑的物理模型(称为“轻绳模型”)
绳约束
内轨道约束
注:“轻绳”只能对小球产生拉力,不能产生支持力。(内轨道约束类似)
mg
O
绳
mg
O
轨道
小球恰好过最高点的条件:
当v=v0,小球恰好能够通过最高点;
当v
最高点:
小球在最低点时:
绳对小球产生竖直向上的拉力(若是内轨道则产生竖直向上的支持力)
v
o
mg
T1
最低点:
v2
mg
T2
L
故
(超重)
2、轻杆(或管道)——小球组成有支撑的物理模型(称为“轻杆模型”)
杆约束
管道约束
注:“轻杆”既能对小球产生拉力,也能产生支持力。(管道约束类似)
物理情景
图示
在最高点的临界特点
做圆周运动条件
细绳拉着小球在竖直平面内运动
T=0
在最高点时速度应不小于
小球在竖直放置的光滑圆环内侧运动
FN=0
在最高点时速度应不小于
小球固定在轻杆上在竖直面内运动
V>0
F向>0
F向=FT+mg 或F向=mg-Fn
在最高点速度应大于0
小球在竖直放置的光滑管中运动
V>0
F向>0
F向=FT+mg 或F向=mg-Fn
在最高点速度应大于0
绳子系着装有水的木桶,在竖直面内做圆周运动,水的质量m=0.5kg,绳子长度为L=60cm,求:
(1)最高点水不留出的最小速度?
(2)设水在最高点速度为v=3m/s,求水对桶底的压力?
(1)在最高点水不流出的最小速率为 m/s.
(2)水对桶底的压力为2.5N.
如图所示,一质量为m的小球,用长为L轻杆固定住,使其在竖直面内作圆周运动.(1)若小球恰好能通过最高点,则小球在最高点是多少?小球的受力情况如何?(2)若小球在最低点受到杆子的拉力为3mg,则小球在最低点的速度是多少?
O
(1)速度为0,受到重力和向上的支持力
(2)
