2020-2021学年青岛新版八年级下册数学第7章 实数单元测试卷(Word版有答案)
文档属性
| 名称 | 2020-2021学年青岛新版八年级下册数学第7章 实数单元测试卷(Word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 288.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-02 00:00:00 | ||
图片预览




文档简介
2020-2021学年青岛新版八年级下册数学《第7章
实数》单元测试卷
一.选择题
1.如图所示,下列存在算术平方根的是( )
A.a﹣b
B.ab
C.b﹣a
D.a+b
2.Rt△ABC的两边长分别为3和4,则第三边长的平方是( )
A.25
B.7
C.12
D.25或7
3.在实数,,,,,0.808008,0.121221222…中,无理数的个数为( )
A.1个
B.2个
C.3个
D.4个
4.三角形的三边长分别是2n+1、2n2+2n、2n2+2n+1(n为自然数),则此三角形是( )
A.直角三角形
B.等腰直角三角形
C.等腰三角形
D.无法判定
5.下列各组数是勾股数的为( )
A.2,4,5
B.8,15,17
C.11,13,15
D.4,5,6
6.下列运算中,不是总能进行的是( )
A.平方
B.立方
C.开平方
D.开立方
7.﹣开立方等于( )
A.﹣8
B.﹣4
C.﹣2
D.±4
8.设0<m<1,则在实数m,,,中,最小的数是( )
A.m
B.
C.
D.
9.2015年4月25号,尼泊尔发生8.1级地震,为了储存救灾物资,特搭建一长方形库房,经测量长为40m,宽为20m,现准备从对角引两条通道,则对角线的长为( )
A.5m
B.10m
C.20m
D.30m
10.观察图形,可以验证( )
A.a2+b2=c2
B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a+b)2=a2+2ab+b2
二.填空题
11.在△ABC中,∠B=90°,a=3,c=4,则b=
.
12.计算:
﹣=
;
=
;
|π﹣3.15|=
;
=
.
13.若|x﹣1|=,则x=
.
14.计算器计算的按键顺序为,其显示结果为
.
15.
的平方根是0,
的平方根是±8.
16.有一圆柱形油罐底面周长为12米,高AB是5米,要以点A环绕油罐建梯子,正好到A点的正上方B点,梯子最短需
米.
17.在,,,,3.14,0,,中,无理数有
个.
18.如图,在3×3的方格纸中,有一个正方形ABCD,这个正方形的面积是
.
19.比较大小:
2;若a>2,则|2﹣a|=
.
20.的倒数是
,()3的相反数是
.
三.解答题
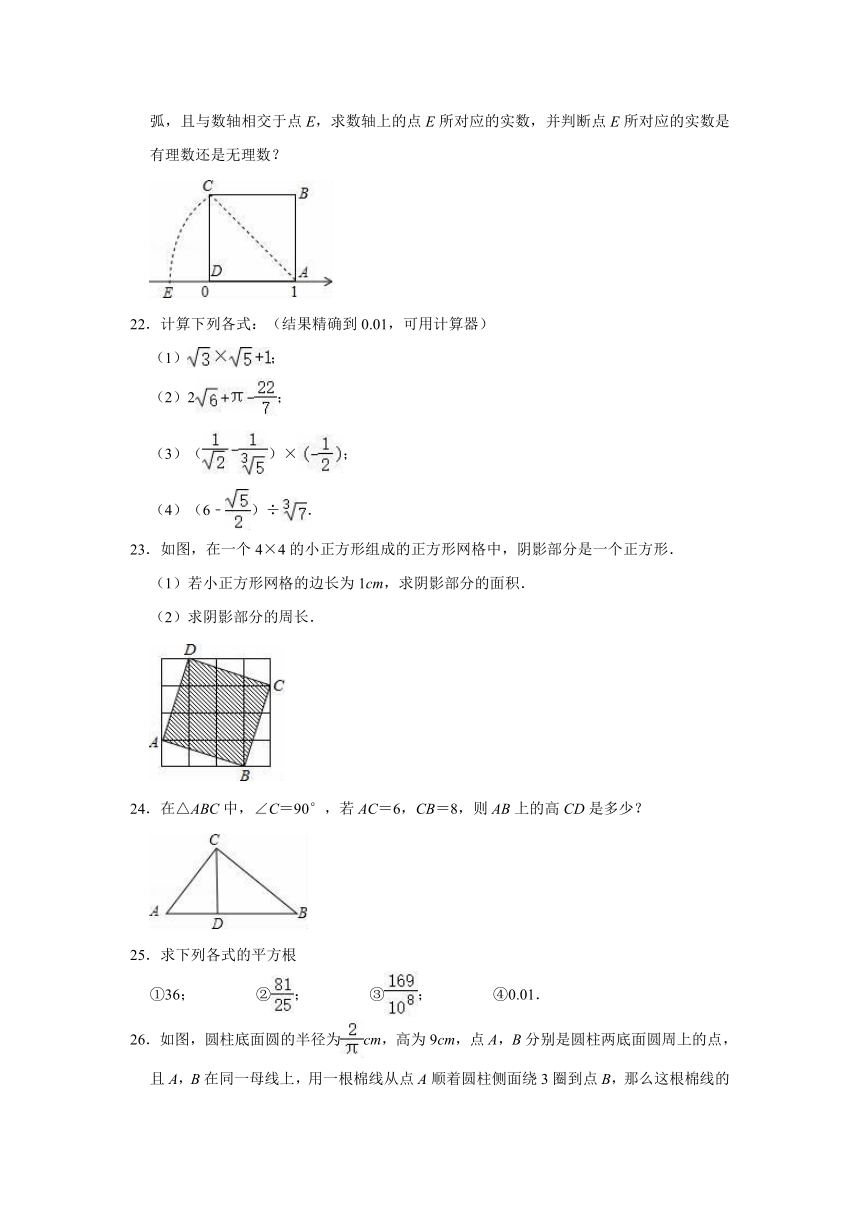
21.如图正方形ABCD一边在以点D为原点的数轴上,以点A为圆心,以AC长为半径画弧,且与数轴相交于点E,求数轴上的点E所对应的实数,并判断点E所对应的实数是有理数还是无理数?
22.计算下列各式:(结果精确到0.01,可用计算器)
(1);
(2)2;
(3)()×;
(4)(6﹣)÷.
23.如图,在一个4×4的小正方形组成的正方形网格中,阴影部分是一个正方形.
(1)若小正方形网格的边长为1cm,求阴影部分的面积.
(2)求阴影部分的周长.
24.在△ABC中,∠C=90°,若AC=6,CB=8,则AB上的高CD是多少?
25.求下列各式的平方根
①36; ②; ③; ④0.01.
26.如图,圆柱底面圆的半径为cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?
27.求x值
(1)2x2=8
(2)x2﹣=0
(3)(2x﹣1)3=﹣8
(4)340+512x3=﹣3.
参考答案与试题解析
一.选择题
1.解:根据数轴可得:a>0,b<0,|a|<|b|,
则:b﹣a<0,a+b<0,a﹣b>0,ab<0,
存在算术平方根的是a﹣b,
故选:A.
2.解:若4为斜边时,根据勾股定理得第三边平方为42﹣32=7;
若4不为斜边,根据勾股定理得第三边平方为42+32=16+9=25,
则第三边的平方为25或7.
故选:D.
3.解:∵实数,,,,,0.808008,0.121221222…中
是开方开不尽的数;,0.121221222…是无限不循环小数故这三个数是无理数.
故选:C.
4.解:∵(2n2+2n)2+(2n+1)2=4n4+4n2+8n3+4n2+4n+1=4n4+8n3+8n2+1;
(2n2+2n+1)2=(2n2+2n+1)(2n2+2n+1)=4n4+8n3+8n2+1;
∴(2n2+2n)2+(2n+1)2=(2n2+2n+1)2,
∴三角形是直角三角形.
故选:A.
5.解:A、22+42=20≠52,故不是;
B、82+152=289=172,故是勾股数;
C、112+132=290≠152,故不是;
D、42+52=41≠62,故不是;
故选:B.
6.解:∵负数没有平方根,∴不是总能进行开平方.
故选:C.
7.解:∵﹣=﹣8,﹣8的立方根是﹣2,
∴﹣开立方等于﹣2;
故选:C.
8.解:∵0<m<1,
∴可以取m=,
则m=,=2,=≈0.707,=>,
∴m最小,
故选:A.
9.解:如图所示:
∵AB=40m,BC=20m,
∴AC===20(m),
故选:C.
10.解:梯形面积=,
三个三角形面积之和=,
,
可得:c2=a2+b2,
故选:A.
二.填空题
11.解:在△ABC中,∠B=90°,由勾股定理得:
b===5;
故答案为:5.
12.解:∵22=2,
∴﹣=﹣2;
∵(±0.11)2=0.0121,
∴±=±0.11;
∵π≈3.14<3.15,
∴|π﹣3.15|=3.15﹣π;
∵4<7<9,
∴2<<3,
∴﹣3<0,
∴|﹣3|=3﹣.
故答案为:﹣2,±0.11,3.15﹣π,3﹣.
13.解:|x﹣1|=,
x﹣1=或x﹣1=﹣,
x=+1,或x=1﹣,
故答案为:
+1,1﹣.
14.解:∵1.3
1.3=1.69,∴√1.69=1.3,故答案为1.3
15.解:0的平方根是0;
∵(±8)2=64,
∴64的平方根是±8.
故答案为:0,64.
16.解:如图,将圆柱体展开,连接A、B,
根据两点之间线段最短,梯子最短是AB===13(m).
答:梯子最短是13米.
故答案为:13.
17.解:所给数据中,无理数有:、、﹣1、,共4个.
故答案为:4.
18.解:这个正方形的面积=3×3﹣4××1×2,
=9﹣4,
=5.
故答案为:5.
19.解:∵,
∴>=2;
∵a>2,
∴2﹣a<0,
∴|2﹣a|=a﹣2.
故答案为:>、a﹣2.
20.解:=﹣,﹣的倒数为﹣3;()3=﹣9,﹣9的相反数为9,
故答案为:﹣3;9
三.解答题
21.解:∵正方形ABCD的边长AD=1,
∴AC==,
∴AE=AC=,
∴DE=AE﹣AD=﹣1,
∵点D在原点,点E在原点的左边,
∴点E所对应的实数为1﹣,是无理数.
22.解:(1)原式=+1
≈4.87;
(2)原式≈2.449+3.142﹣3.143
≈2.45;
(3)原式=﹣+
≈﹣0.354+0.292
=﹣0.06;
(4)原式≈(6﹣1.118)÷1.913
=4.882÷1.913
≈2.55.
23.解:(1)∵阴影部分正方形的边长AB==cm,
∴阴影部分的面积=×=10cm2.
(2)∵阴影部分正方形的边长AB==cm,
∴阴影部分的周长=4cm.
24.解:∵在△ABC中,∠C=90°,AC=6,CB=8,
∴AB==10,
∵S△ACB=×AC×BC=AB×CD,
∴AC×BC=AB×CD,即6×8=10×CD,
∴CD=4.8.
故AB上的高CD是4.8.
25.解:①=±6;
②=±;
③±=;
④=±0.1
26.解:圆柱体的展开图如图所示:
用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→C'D'→DB,
即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短,
∵圆柱底面半径为cm,
∴长方形的宽即是圆柱体的底面周长=2π×=4cm,
又∵圆柱高为9cm,
∴小长方形的一条边长是3cm,
根据勾股定理求得AC=C'D'=DB=5cm,
∴AC+C'D'+DB=15cm,
答:这根棉线的长度最短是15cm.
27.解:(1)方程变形得:x2=4,
开方得:x=2或x=﹣2;
(2)方程变形得:x2=,
开方得:x=±;
(3)(2x﹣1)3=﹣8,
开立方得:2x﹣1=﹣2,
解得:x=﹣;
(4)x3=﹣,
开立方得:x=﹣.
实数》单元测试卷
一.选择题
1.如图所示,下列存在算术平方根的是( )
A.a﹣b
B.ab
C.b﹣a
D.a+b
2.Rt△ABC的两边长分别为3和4,则第三边长的平方是( )
A.25
B.7
C.12
D.25或7
3.在实数,,,,,0.808008,0.121221222…中,无理数的个数为( )
A.1个
B.2个
C.3个
D.4个
4.三角形的三边长分别是2n+1、2n2+2n、2n2+2n+1(n为自然数),则此三角形是( )
A.直角三角形
B.等腰直角三角形
C.等腰三角形
D.无法判定
5.下列各组数是勾股数的为( )
A.2,4,5
B.8,15,17
C.11,13,15
D.4,5,6
6.下列运算中,不是总能进行的是( )
A.平方
B.立方
C.开平方
D.开立方
7.﹣开立方等于( )
A.﹣8
B.﹣4
C.﹣2
D.±4
8.设0<m<1,则在实数m,,,中,最小的数是( )
A.m
B.
C.
D.
9.2015年4月25号,尼泊尔发生8.1级地震,为了储存救灾物资,特搭建一长方形库房,经测量长为40m,宽为20m,现准备从对角引两条通道,则对角线的长为( )
A.5m
B.10m
C.20m
D.30m
10.观察图形,可以验证( )
A.a2+b2=c2
B.(a﹣b)2=a2﹣2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a+b)2=a2+2ab+b2
二.填空题
11.在△ABC中,∠B=90°,a=3,c=4,则b=
.
12.计算:
﹣=
;
=
;
|π﹣3.15|=
;
=
.
13.若|x﹣1|=,则x=
.
14.计算器计算的按键顺序为,其显示结果为
.
15.
的平方根是0,
的平方根是±8.
16.有一圆柱形油罐底面周长为12米,高AB是5米,要以点A环绕油罐建梯子,正好到A点的正上方B点,梯子最短需
米.
17.在,,,,3.14,0,,中,无理数有
个.
18.如图,在3×3的方格纸中,有一个正方形ABCD,这个正方形的面积是
.
19.比较大小:
2;若a>2,则|2﹣a|=
.
20.的倒数是
,()3的相反数是
.
三.解答题
21.如图正方形ABCD一边在以点D为原点的数轴上,以点A为圆心,以AC长为半径画弧,且与数轴相交于点E,求数轴上的点E所对应的实数,并判断点E所对应的实数是有理数还是无理数?
22.计算下列各式:(结果精确到0.01,可用计算器)
(1);
(2)2;
(3)()×;
(4)(6﹣)÷.
23.如图,在一个4×4的小正方形组成的正方形网格中,阴影部分是一个正方形.
(1)若小正方形网格的边长为1cm,求阴影部分的面积.
(2)求阴影部分的周长.
24.在△ABC中,∠C=90°,若AC=6,CB=8,则AB上的高CD是多少?
25.求下列各式的平方根
①36; ②; ③; ④0.01.
26.如图,圆柱底面圆的半径为cm,高为9cm,点A,B分别是圆柱两底面圆周上的点,且A,B在同一母线上,用一根棉线从点A顺着圆柱侧面绕3圈到点B,那么这根棉线的长度最短是多少?
27.求x值
(1)2x2=8
(2)x2﹣=0
(3)(2x﹣1)3=﹣8
(4)340+512x3=﹣3.
参考答案与试题解析
一.选择题
1.解:根据数轴可得:a>0,b<0,|a|<|b|,
则:b﹣a<0,a+b<0,a﹣b>0,ab<0,
存在算术平方根的是a﹣b,
故选:A.
2.解:若4为斜边时,根据勾股定理得第三边平方为42﹣32=7;
若4不为斜边,根据勾股定理得第三边平方为42+32=16+9=25,
则第三边的平方为25或7.
故选:D.
3.解:∵实数,,,,,0.808008,0.121221222…中
是开方开不尽的数;,0.121221222…是无限不循环小数故这三个数是无理数.
故选:C.
4.解:∵(2n2+2n)2+(2n+1)2=4n4+4n2+8n3+4n2+4n+1=4n4+8n3+8n2+1;
(2n2+2n+1)2=(2n2+2n+1)(2n2+2n+1)=4n4+8n3+8n2+1;
∴(2n2+2n)2+(2n+1)2=(2n2+2n+1)2,
∴三角形是直角三角形.
故选:A.
5.解:A、22+42=20≠52,故不是;
B、82+152=289=172,故是勾股数;
C、112+132=290≠152,故不是;
D、42+52=41≠62,故不是;
故选:B.
6.解:∵负数没有平方根,∴不是总能进行开平方.
故选:C.
7.解:∵﹣=﹣8,﹣8的立方根是﹣2,
∴﹣开立方等于﹣2;
故选:C.
8.解:∵0<m<1,
∴可以取m=,
则m=,=2,=≈0.707,=>,
∴m最小,
故选:A.
9.解:如图所示:
∵AB=40m,BC=20m,
∴AC===20(m),
故选:C.
10.解:梯形面积=,
三个三角形面积之和=,
,
可得:c2=a2+b2,
故选:A.
二.填空题
11.解:在△ABC中,∠B=90°,由勾股定理得:
b===5;
故答案为:5.
12.解:∵22=2,
∴﹣=﹣2;
∵(±0.11)2=0.0121,
∴±=±0.11;
∵π≈3.14<3.15,
∴|π﹣3.15|=3.15﹣π;
∵4<7<9,
∴2<<3,
∴﹣3<0,
∴|﹣3|=3﹣.
故答案为:﹣2,±0.11,3.15﹣π,3﹣.
13.解:|x﹣1|=,
x﹣1=或x﹣1=﹣,
x=+1,或x=1﹣,
故答案为:
+1,1﹣.
14.解:∵1.3
1.3=1.69,∴√1.69=1.3,故答案为1.3
15.解:0的平方根是0;
∵(±8)2=64,
∴64的平方根是±8.
故答案为:0,64.
16.解:如图,将圆柱体展开,连接A、B,
根据两点之间线段最短,梯子最短是AB===13(m).
答:梯子最短是13米.
故答案为:13.
17.解:所给数据中,无理数有:、、﹣1、,共4个.
故答案为:4.
18.解:这个正方形的面积=3×3﹣4××1×2,
=9﹣4,
=5.
故答案为:5.
19.解:∵,
∴>=2;
∵a>2,
∴2﹣a<0,
∴|2﹣a|=a﹣2.
故答案为:>、a﹣2.
20.解:=﹣,﹣的倒数为﹣3;()3=﹣9,﹣9的相反数为9,
故答案为:﹣3;9
三.解答题
21.解:∵正方形ABCD的边长AD=1,
∴AC==,
∴AE=AC=,
∴DE=AE﹣AD=﹣1,
∵点D在原点,点E在原点的左边,
∴点E所对应的实数为1﹣,是无理数.
22.解:(1)原式=+1
≈4.87;
(2)原式≈2.449+3.142﹣3.143
≈2.45;
(3)原式=﹣+
≈﹣0.354+0.292
=﹣0.06;
(4)原式≈(6﹣1.118)÷1.913
=4.882÷1.913
≈2.55.
23.解:(1)∵阴影部分正方形的边长AB==cm,
∴阴影部分的面积=×=10cm2.
(2)∵阴影部分正方形的边长AB==cm,
∴阴影部分的周长=4cm.
24.解:∵在△ABC中,∠C=90°,AC=6,CB=8,
∴AB==10,
∵S△ACB=×AC×BC=AB×CD,
∴AC×BC=AB×CD,即6×8=10×CD,
∴CD=4.8.
故AB上的高CD是4.8.
25.解:①=±6;
②=±;
③±=;
④=±0.1
26.解:圆柱体的展开图如图所示:
用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→C'D'→DB,
即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短,
∵圆柱底面半径为cm,
∴长方形的宽即是圆柱体的底面周长=2π×=4cm,
又∵圆柱高为9cm,
∴小长方形的一条边长是3cm,
根据勾股定理求得AC=C'D'=DB=5cm,
∴AC+C'D'+DB=15cm,
答:这根棉线的长度最短是15cm.
27.解:(1)方程变形得:x2=4,
开方得:x=2或x=﹣2;
(2)方程变形得:x2=,
开方得:x=±;
(3)(2x﹣1)3=﹣8,
开立方得:2x﹣1=﹣2,
解得:x=﹣;
(4)x3=﹣,
开立方得:x=﹣.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
