5.1.1相交线-2020-2021学年人教版七年级数学下册课件(16张)
文档属性
| 名称 | 5.1.1相交线-2020-2021学年人教版七年级数学下册课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-02 00:00:00 | ||
图片预览

文档简介
(共16张PPT)
5.1.1相交线
合作探究,获取新知
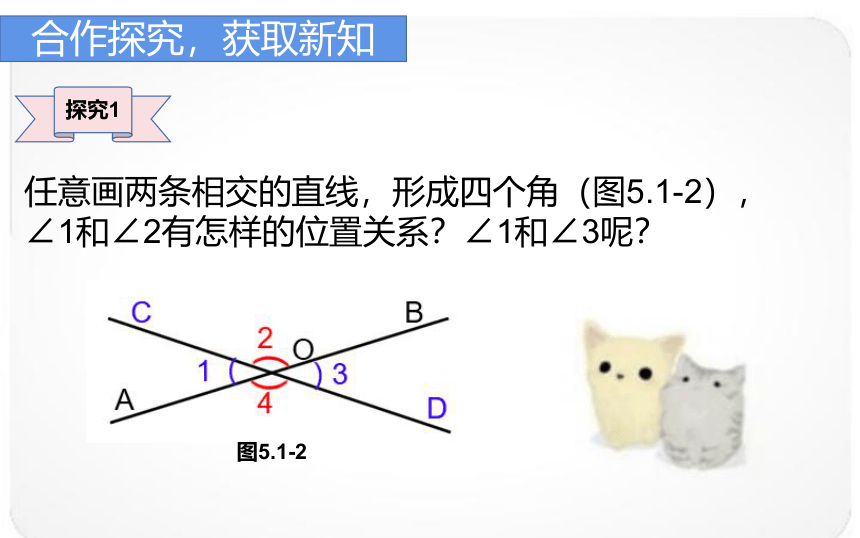
探究1
任意画两条相交的直线,形成四个角(图5.1-2),
∠1和∠2有怎样的位置关系?∠1和∠3呢?
图5.1-2
图5.1-2
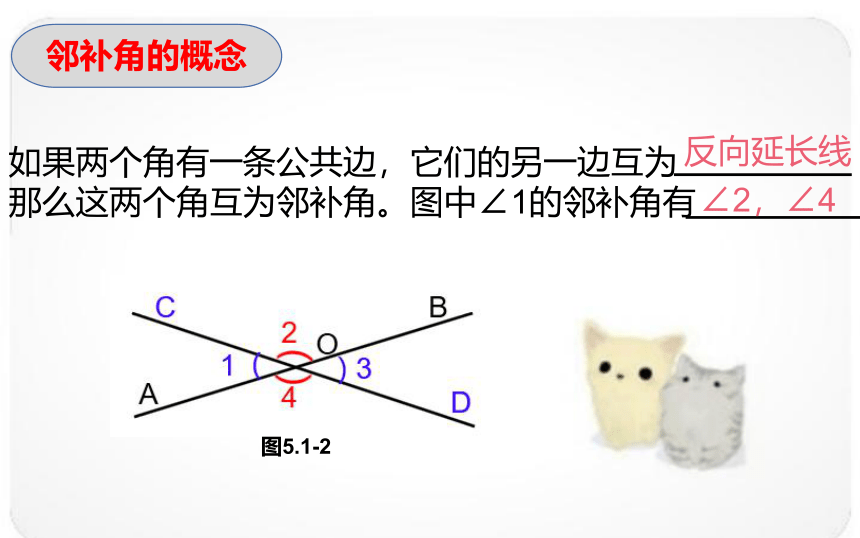
邻补角的概念
如果两个角有一条公共边,它们的另一边互为
那么这两个角互为邻补角。图中∠1的邻补角有
反向延长线
∠2,∠4
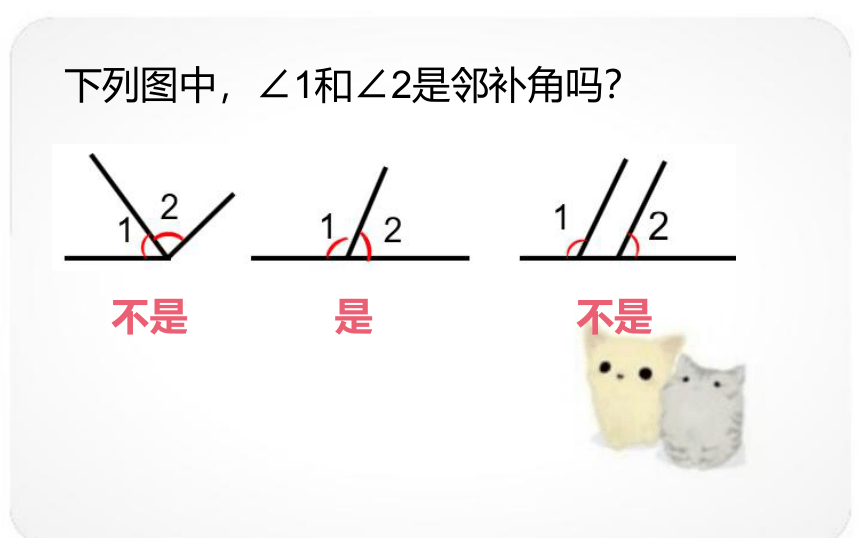
下列图中,∠1和∠2是邻补角吗?
不是
不是
是
图5.1-2
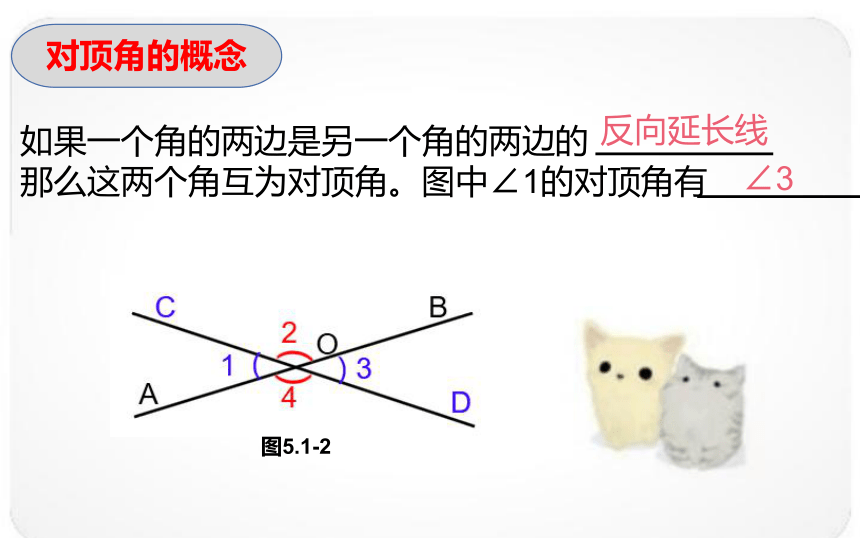
对顶角的概念
如果一个角的两边是另一个角的两边的
那么这两个角互为对顶角。图中∠1的对顶角有
反向延长线
∠3
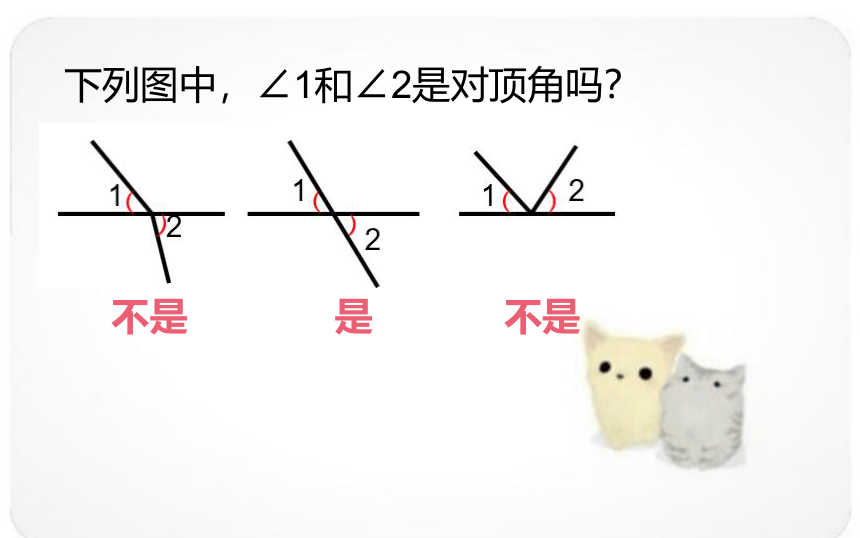
下列图中,∠1和∠2是对顶角吗?
不是
不是
是
合作探究,获取新知
探究2
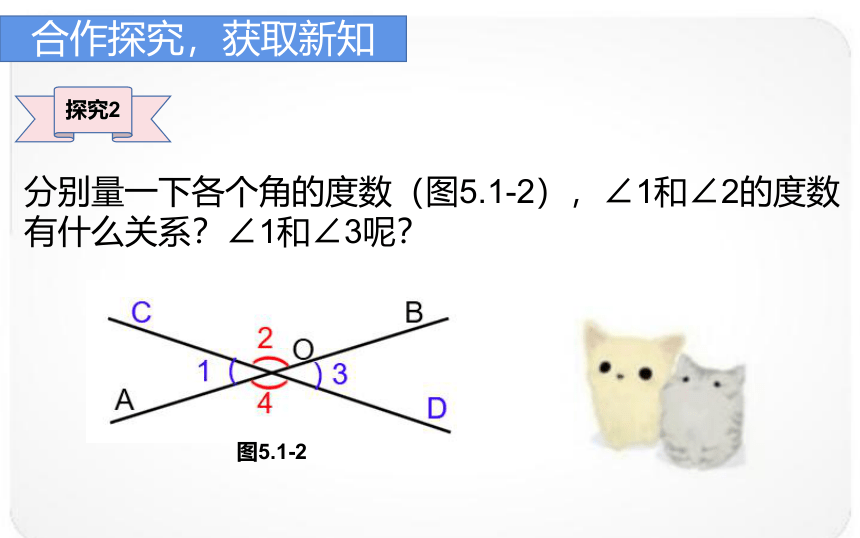
分别量一下各个角的度数(图5.1-2),∠1和∠2的度数
有什么关系?∠1和∠3呢?
图5.1-2
图5.1-2
邻补角的性质
互为邻补角的两个角的和为180°
图5.1-2
问题:如图,∠1和∠3在数量上又有什么关系呢?
证明
图5.1-2
对顶角的性质
对顶角相等
例2
如图,直线AB,CD,EF相交于点O
(1)写出∠AOC,∠BOE的邻补角
(2)写出∠DOA,∠EOC的对顶角
解:
(1)∠AOC的邻补角是∠AOD,∠COB
∠BOE的邻补角是∠EOA,∠BOF
(2)∠DOA的对顶角是∠COB,
∠EOC的对顶角∠DOF
例3
如图,直线AB,CD交EF于点G,H
∠2=∠3,∠1=70°,求∠4的度数
解:∵∠2=∠
(
)
∠1=70°(
)
∴∠2=
(等量代换)
又∵∠2=∠3(已知)
∴∠3=
(
)
∴∠4=180°-∠
=
(
)
1
对顶角相等
已知
70°
70°
等量代换
3
110°
邻补角的定义
归纳
延长AO到点C,
延长BO到点D
测量∠COD的度数
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量?
C
D
在下图中,花坛转角按图纸要求这个角(图中红色部分)
为135°,施工结束后,要求你检测它是否和合格?请你
设计检测的方法。
5.1.1相交线
合作探究,获取新知
探究1
任意画两条相交的直线,形成四个角(图5.1-2),
∠1和∠2有怎样的位置关系?∠1和∠3呢?
图5.1-2
图5.1-2
邻补角的概念
如果两个角有一条公共边,它们的另一边互为
那么这两个角互为邻补角。图中∠1的邻补角有
反向延长线
∠2,∠4
下列图中,∠1和∠2是邻补角吗?
不是
不是
是
图5.1-2
对顶角的概念
如果一个角的两边是另一个角的两边的
那么这两个角互为对顶角。图中∠1的对顶角有
反向延长线
∠3
下列图中,∠1和∠2是对顶角吗?
不是
不是
是
合作探究,获取新知
探究2
分别量一下各个角的度数(图5.1-2),∠1和∠2的度数
有什么关系?∠1和∠3呢?
图5.1-2
图5.1-2
邻补角的性质
互为邻补角的两个角的和为180°
图5.1-2
问题:如图,∠1和∠3在数量上又有什么关系呢?
证明
图5.1-2
对顶角的性质
对顶角相等
例2
如图,直线AB,CD,EF相交于点O
(1)写出∠AOC,∠BOE的邻补角
(2)写出∠DOA,∠EOC的对顶角
解:
(1)∠AOC的邻补角是∠AOD,∠COB
∠BOE的邻补角是∠EOA,∠BOF
(2)∠DOA的对顶角是∠COB,
∠EOC的对顶角∠DOF
例3
如图,直线AB,CD交EF于点G,H
∠2=∠3,∠1=70°,求∠4的度数
解:∵∠2=∠
(
)
∠1=70°(
)
∴∠2=
(等量代换)
又∵∠2=∠3(已知)
∴∠3=
(
)
∴∠4=180°-∠
=
(
)
1
对顶角相等
已知
70°
70°
等量代换
3
110°
邻补角的定义
归纳
延长AO到点C,
延长BO到点D
测量∠COD的度数
要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量?
C
D
在下图中,花坛转角按图纸要求这个角(图中红色部分)
为135°,施工结束后,要求你检测它是否和合格?请你
设计检测的方法。
