解直角三角形复习(一)
图片预览


文档简介
(共13张PPT)
A
B
b
a
c
┏
C
(一)
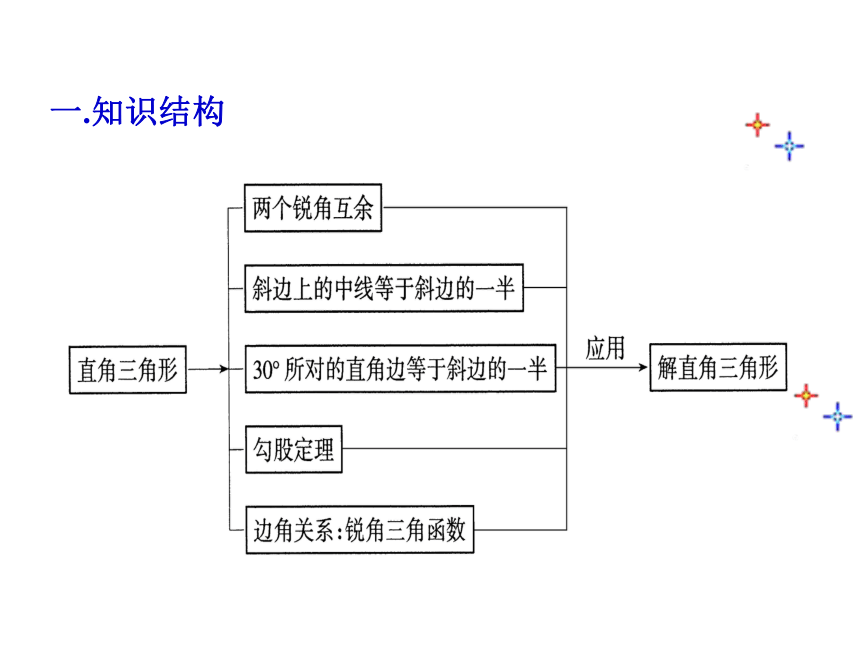
一.知识结构
二、知识要点回顾
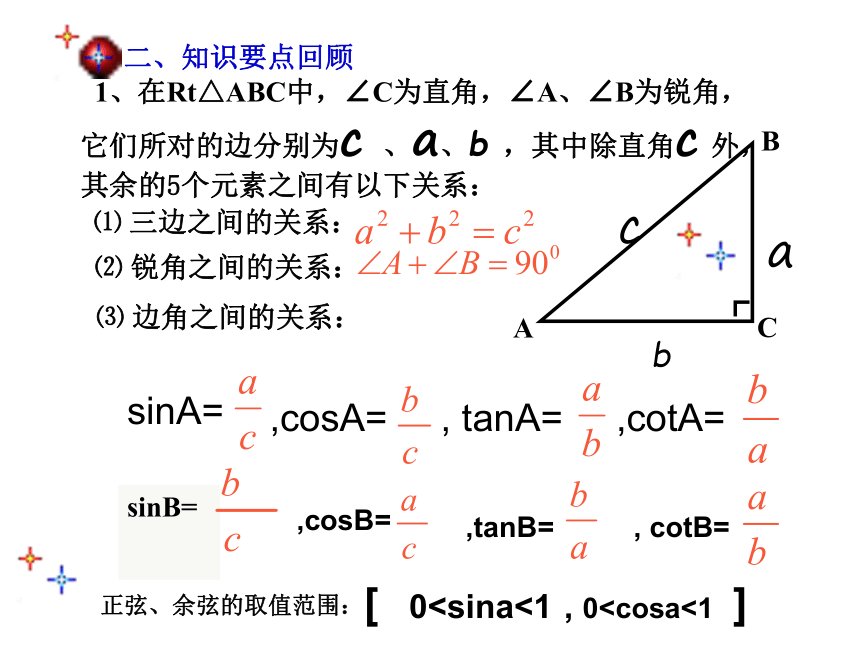
1、在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c 、a、b ,其中除直角c 外,
其余的5个元素之间有以下关系:
⑴ 三边之间的关系:
⑵ 锐角之间的关系:
⑶ 边角之间的关系:
A
B
b
a
c
┏
C
sinB=
[ 0sinA=
,cosA= , tanA= ,cotA=
,cosB=
,tanB= , cotB=
正弦、余弦的取值范围:
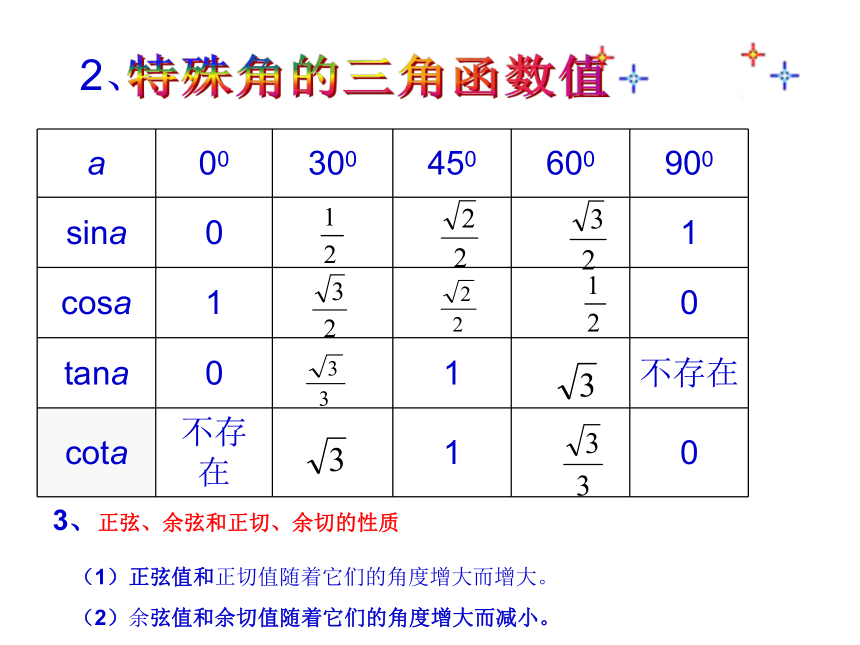
a 00 300 450 600 900
sina 0 1
cosa 1 0
tana 0 1 不存在
cota 不存在 1 0
2、
3、正弦、余弦和正切、余切的性质
(1)正弦值和正切值随着它们的角度增大而增大。
(2)余弦值和余切值随着它们的角度增大而减小。
4、同角的三角函数关系:
(1)平方关系:
(2) 倒数关系:
(3)商数关系:
(4)余角函数之间的关系:
sinA=sin(90o_B)=cosB, cosA=cos(900_B)=sinB,
tanA=tan(900_B)=cotB, cotA=cot(900_B)=tanB
☆ 例题1
1.已知角,求值
求下列各式的值
2sin30°+3tan30°+cot45°
=2 + d
cos245°+ tan60°cos30°
= 2
3.
= 3 - o
1.
2.
☆ 例题2
1.已知角,求值
求锐角A的值
2.已知值,求角
1. 已知 tanA= ,求锐角A .
已知2cosA - = 0 ,
求锐角A的度数 .
∠A=60°
∠A=30°
解:∵ 2cosA - = 0
∴ 2cosA =
∴cosA= ∴∠A= 30°
☆ 例题3
1.已知角,求值
确定值、角的范围
2.已知值,求角
1. 在Rt△ABC中∠C=90°,当 锐角A>45°时,sinA的值( )
3. 确定值、角的范围
(A)0<sinA< (B) <sinA<1
(C) 0<sinA< (D) <sinA<1
D
当∠A为锐角,且cotA的值小于 时,
∠A( )
(A)0°<∠A<30° (B)30°<∠A<90°
(C) 0°<∠A<60°(D)60°<∠A<90°
B
练习
1. 在△ABC中∠C=90° ,∠B=2∠A . 则cosA=______
2. 若tan(β+20°)= ,为锐角.则β=______
3.在Rt△ABC中,∠C=90°,cosB= ,则sinB的值为_______.
40°
4. tana.tan20°=1,则a= 度
70°
例题4 在Rt△ABC中,∠C=90°:
⑴已知∠A、 c, 则a=__________;b=_________。
⑵已知∠A、 b, 则a=__________;c=_________。
⑶已知∠A、 a,则b=__________;c=_________。
(4)已知a、c,则b=__________ 。
A
B
b
a
c
┏
C
⌒
对边
邻边
斜边
已知一锐角、斜边,求对边,用锐角的正弦;
求邻边,用锐角的余弦。
已知一锐角、邻边,求对边,用锐角的正切;
求斜边,用锐角的余弦。
已知一锐角、对边,求邻边,用锐角的余切;
求斜边,用锐角的正弦。
已知任意两边,求第三边,用勾股定理
小结
内容小结
本节课主要复习了两个部分的内容:一部分是本章的知识结构和要点;另一部分是直角三角形简单基础知识的应用。
方法归纳
1.一是把直角三角形中简单基础知识通过数学模型加强理解识记,二是将已知条件转化为示意图中的边、角或它们之间的关系。
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形。同时在解的过程中可以用方程的思想解题。
A
B
b
a
c
┏
C
(一)
一.知识结构
二、知识要点回顾
1、在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
它们所对的边分别为c 、a、b ,其中除直角c 外,
其余的5个元素之间有以下关系:
⑴ 三边之间的关系:
⑵ 锐角之间的关系:
⑶ 边角之间的关系:
A
B
b
a
c
┏
C
sinB=
[ 0
,cosA= , tanA= ,cotA=
,cosB=
,tanB= , cotB=
正弦、余弦的取值范围:
a 00 300 450 600 900
sina 0 1
cosa 1 0
tana 0 1 不存在
cota 不存在 1 0
2、
3、正弦、余弦和正切、余切的性质
(1)正弦值和正切值随着它们的角度增大而增大。
(2)余弦值和余切值随着它们的角度增大而减小。
4、同角的三角函数关系:
(1)平方关系:
(2) 倒数关系:
(3)商数关系:
(4)余角函数之间的关系:
sinA=sin(90o_B)=cosB, cosA=cos(900_B)=sinB,
tanA=tan(900_B)=cotB, cotA=cot(900_B)=tanB
☆ 例题1
1.已知角,求值
求下列各式的值
2sin30°+3tan30°+cot45°
=2 + d
cos245°+ tan60°cos30°
= 2
3.
= 3 - o
1.
2.
☆ 例题2
1.已知角,求值
求锐角A的值
2.已知值,求角
1. 已知 tanA= ,求锐角A .
已知2cosA - = 0 ,
求锐角A的度数 .
∠A=60°
∠A=30°
解:∵ 2cosA - = 0
∴ 2cosA =
∴cosA= ∴∠A= 30°
☆ 例题3
1.已知角,求值
确定值、角的范围
2.已知值,求角
1. 在Rt△ABC中∠C=90°,当 锐角A>45°时,sinA的值( )
3. 确定值、角的范围
(A)0<sinA< (B) <sinA<1
(C) 0<sinA< (D) <sinA<1
D
当∠A为锐角,且cotA的值小于 时,
∠A( )
(A)0°<∠A<30° (B)30°<∠A<90°
(C) 0°<∠A<60°(D)60°<∠A<90°
B
练习
1. 在△ABC中∠C=90° ,∠B=2∠A . 则cosA=______
2. 若tan(β+20°)= ,为锐角.则β=______
3.在Rt△ABC中,∠C=90°,cosB= ,则sinB的值为_______.
40°
4. tana.tan20°=1,则a= 度
70°
例题4 在Rt△ABC中,∠C=90°:
⑴已知∠A、 c, 则a=__________;b=_________。
⑵已知∠A、 b, 则a=__________;c=_________。
⑶已知∠A、 a,则b=__________;c=_________。
(4)已知a、c,则b=__________ 。
A
B
b
a
c
┏
C
⌒
对边
邻边
斜边
已知一锐角、斜边,求对边,用锐角的正弦;
求邻边,用锐角的余弦。
已知一锐角、邻边,求对边,用锐角的正切;
求斜边,用锐角的余弦。
已知一锐角、对边,求邻边,用锐角的余切;
求斜边,用锐角的正弦。
已知任意两边,求第三边,用勾股定理
小结
内容小结
本节课主要复习了两个部分的内容:一部分是本章的知识结构和要点;另一部分是直角三角形简单基础知识的应用。
方法归纳
1.一是把直角三角形中简单基础知识通过数学模型加强理解识记,二是将已知条件转化为示意图中的边、角或它们之间的关系。
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形。同时在解的过程中可以用方程的思想解题。
