2020-2021学年八年级下学期数学青岛版6.2 平行四边形的判定课件(15张)
文档属性
| 名称 | 2020-2021学年八年级下学期数学青岛版6.2 平行四边形的判定课件(15张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 687.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-02 00:00:00 | ||
图片预览





文档简介
6.2 平行四边形的判定
学习目标
掌握平行四边形的判定方法并能灵活运用
经历探索、猜想、证明的过程,进一步发展推理论证的能力
体会在证明过程中所运用的归纳、类比、转化等数学思想方法
回顾一下:平行四边形的定义和性质分别是什么?
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形
平行四边形的性质1:平行四边形的对边相等
平行四边形的性质2:平行四边形的对角相等
平行四边形的性质3:平行四边形的对角线互相平分
怎样判定一个四边形是平行四边形呢?
利用定义,我们知道,对边平行的四边形是平行四边形
除了运用平行四边形的定义外,还有其他方法么?
根据平行四边形的定义,两组对边分别平行的四边形是平行四边形。
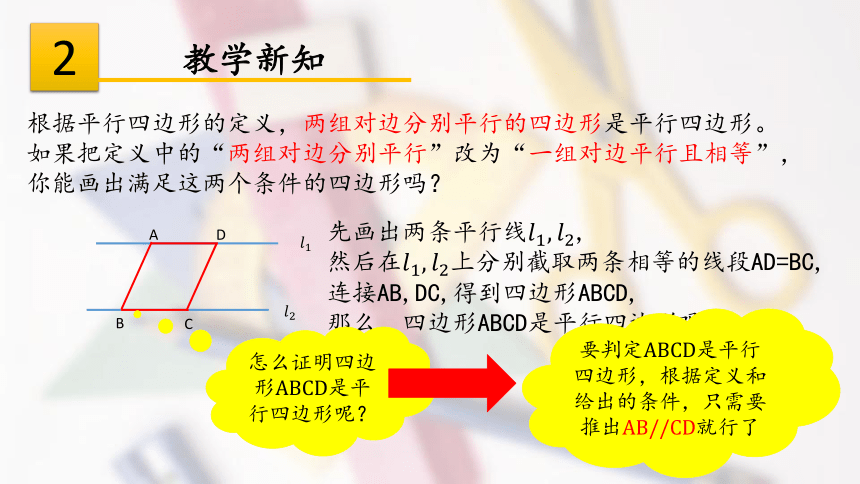
如果把定义中的“两组对边分别平行”改为“一组对边平行且相等”,你能画出满足这两个条件的四边形吗?
A
D
B
C
????1
?
????2
?
先画出两条平行线????1,????2,
然后在????1,????2上分别截取两条相等的线段AD=BC,
连接AB,DC,得到四边形ABCD,
那么,四边形ABCD是平行四边形吗?
?
怎么证明四边形ABCD是平行四边形呢?
要判定ABCD是平行四边形,根据定义和给出的条件,只需要推出AB//CD就行了
已知:如图,在四边形ABCD中,AD//BC,AD=BC.
求证:四边形ABCD是平行四边形
证明:连接AC
∵AD//BC
∴∠1=∠2
∵AD=BC,AC=CA
∴△CDA≌△ABC(SAS)
∴∠3=∠4
∴AB//CD
∴四边形ABCD是平行四边形
A
D
B
C
1
4
3
2
于是,就得到
平行四边形的判定定理1
一组对边平行且相等的四边形是平行四边形
几何语言: ∵AD//BC,AD=BC
∴四边形ABCD是平行四边形
利用平行四边形的定义,即两组对边的位置关系(分别平行)可以判定四边形是平行四边形。
判定定理1是通过一组对边的位置关系(平行)和数量关系(相等),推出另一组对边的平行关系。
能不能通过两组对边分别相等推出其中一组对边平行呢?
任意画一个∠B,在∠B的两边上分别人去两点A,C,
以点A为圆心,BC的长为半径作弧,
再以点C为圆心,BA的长为半径画弧,记两弧的交点为D,
连接AD,CD便得到四边形ABCD,满足AB=CD,AD=BC。
那么,得到的四边形ABCD是平行四边形吗?
B
A
C
D
怎么证明四边形ABCD是平行四边形?
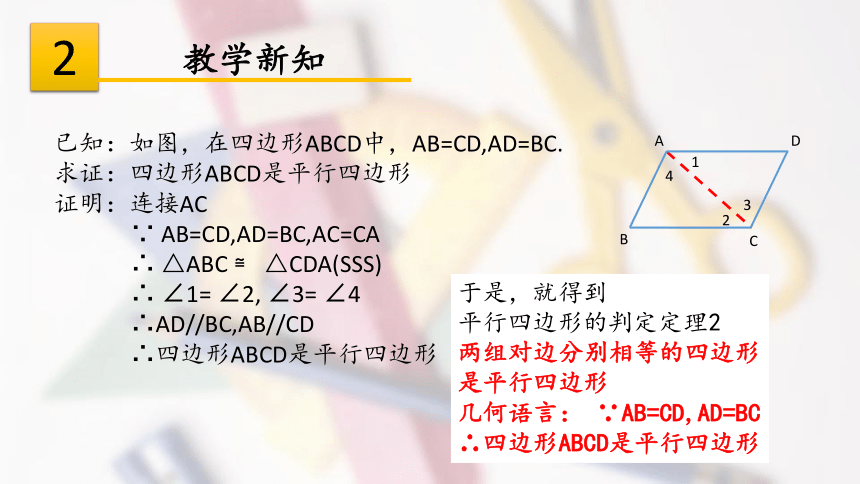
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形
证明:连接AC
∵ AB=CD,AD=BC,AC=CA
∴ △ABC ≌ △CDA(SSS)
∴ ∠1= ∠2, ∠3= ∠4
∴AD//BC,AB//CD
∴四边形ABCD是平行四边形
A
D
B
C
1
4
3
2
于是,就得到
平行四边形的判定定理2
两组对边分别相等的四边形是平行四边形
几何语言: ∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
平行四边形的判定定理1
一组对边平行且相等的四边形是平行四边形
几何语言: ∵AD//BC,AD=BC
∴四边形ABCD是平行四边形
平行四边形的判定定理2
两组对边分别相等的四边形是平行四边形
几何语言: ∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
想一想,判定定理1和判定定理2有什么关系?
已知一组对边相等,要想证明是平行四边形,只需证明另一组对边相等或者是该组对边平行
想一想,两组对角相等的四边形是平行四边形吗?
已知:如图,在四边形ABCD中,∠A=∠C, ∠B=∠D
求证:四边形ABCD是平行四边形
证明:∵∠A=∠C,,∠B=∠D,∠A+∠B+∠C+∠D=360°
∴2∠A+2∠B=360°
∴∠A+∠B=180°
∴AD//BC
同理可证AB//CD
∴四边形ABCD是平行四边形
于是,就得到
两组对角相等的四边形是平行四边形
A
D
B
C
已知:如图,E,F,G,H分别是平行四边形ABCD的边AD,AB,BC,CD上的点,且AE=CG,BF=DH.
求证:四边形EFGH是平行四边形
证明:∵四边形ABCD是平行四边形
∴∠A=∠C,AB=CD
∵BF=DH
∴AF=CH
∵AE=CG
∴△AFE≌△CHG(ASA)
∴EF=GH
同理,FG=HE
∴四边形EFGH是平行四边形
小亮猜测:“在四边形中,能否根据一组对边相等,另一组对边平行,判断这个四边形是平行四边形呢?”
小亮的猜测正确吗?如果正确,请给出正面;如果不正确,请举出反例.
不正确,反例是等腰梯形
1.如图,在四边形ABCD中,∠ADB=∠CBD, ∠ABD=∠CDB.利用三种方法证明四边形ABCD是平行四边形。
方法一:证明:∵∠ADB=∠CBD
∴AD//BC
∵∠ABD=∠CDB
∴AB//CD
∴四边形ABCD是平行四边形
方法二:证明:∵∠ADB=∠CBD,BD=DB,∠ABD=∠CDB
∴△ABD≌△CDB(ASA)
∴AB=CD,AD=CB
∴四边形ABCD是平行四边形
方法三:证明:∵∠ADB=∠CBD,BD=DB,∠ABD=∠CDB
∴△ABD≌△CDB(ASA)
∴AB=CD,AD=CB
∵∠ABD=∠CDB
∴AB//CD
∴四边形ABCD是平行四边形
2.如图,在平行四边形ABCD中,点E,F分别是AD,BC的中点。分别利用判定定理1和判定定理2证明四边形BEDF是平行四边形。
方法一:∵四边形ABCD是平行四边形
∴AD//BC,AD=BC
∵点E,F分别是AD,BC的中点
∴DE=12????????,????????=12BC
∴DE=BF
∴四边形BEDF是平行四边形
?
方法二:∵四边形ABCD是平行四边形
∴AB=CD,AD=BC, ∠A=∠C
∵点E,F分别是AD,BC的中点
∴DE=12????????,????????=12BC
∴AE=DE=BF=CF
∴△ABE≌△CDF(SAS)
∴BE=DF
∴四边形BEDF是平行四边形
?
平行四边形的判定定理1
一组对边平行且相等的四边形是平行四边形
几何语言: ∵AD//BC,AD=BC
∴四边形ABCD是平行四边形
平行四边形的判定定理2
两组对边分别相等的四边形是平行四边形
几何语言: ∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
课本P15,复习与巩固 第1题,第2题
学习目标
掌握平行四边形的判定方法并能灵活运用
经历探索、猜想、证明的过程,进一步发展推理论证的能力
体会在证明过程中所运用的归纳、类比、转化等数学思想方法
回顾一下:平行四边形的定义和性质分别是什么?
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形
平行四边形的性质1:平行四边形的对边相等
平行四边形的性质2:平行四边形的对角相等
平行四边形的性质3:平行四边形的对角线互相平分
怎样判定一个四边形是平行四边形呢?
利用定义,我们知道,对边平行的四边形是平行四边形
除了运用平行四边形的定义外,还有其他方法么?
根据平行四边形的定义,两组对边分别平行的四边形是平行四边形。
如果把定义中的“两组对边分别平行”改为“一组对边平行且相等”,你能画出满足这两个条件的四边形吗?
A
D
B
C
????1
?
????2
?
先画出两条平行线????1,????2,
然后在????1,????2上分别截取两条相等的线段AD=BC,
连接AB,DC,得到四边形ABCD,
那么,四边形ABCD是平行四边形吗?
?
怎么证明四边形ABCD是平行四边形呢?
要判定ABCD是平行四边形,根据定义和给出的条件,只需要推出AB//CD就行了
已知:如图,在四边形ABCD中,AD//BC,AD=BC.
求证:四边形ABCD是平行四边形
证明:连接AC
∵AD//BC
∴∠1=∠2
∵AD=BC,AC=CA
∴△CDA≌△ABC(SAS)
∴∠3=∠4
∴AB//CD
∴四边形ABCD是平行四边形
A
D
B
C
1
4
3
2
于是,就得到
平行四边形的判定定理1
一组对边平行且相等的四边形是平行四边形
几何语言: ∵AD//BC,AD=BC
∴四边形ABCD是平行四边形
利用平行四边形的定义,即两组对边的位置关系(分别平行)可以判定四边形是平行四边形。
判定定理1是通过一组对边的位置关系(平行)和数量关系(相等),推出另一组对边的平行关系。
能不能通过两组对边分别相等推出其中一组对边平行呢?
任意画一个∠B,在∠B的两边上分别人去两点A,C,
以点A为圆心,BC的长为半径作弧,
再以点C为圆心,BA的长为半径画弧,记两弧的交点为D,
连接AD,CD便得到四边形ABCD,满足AB=CD,AD=BC。
那么,得到的四边形ABCD是平行四边形吗?
B
A
C
D
怎么证明四边形ABCD是平行四边形?
已知:如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形
证明:连接AC
∵ AB=CD,AD=BC,AC=CA
∴ △ABC ≌ △CDA(SSS)
∴ ∠1= ∠2, ∠3= ∠4
∴AD//BC,AB//CD
∴四边形ABCD是平行四边形
A
D
B
C
1
4
3
2
于是,就得到
平行四边形的判定定理2
两组对边分别相等的四边形是平行四边形
几何语言: ∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
平行四边形的判定定理1
一组对边平行且相等的四边形是平行四边形
几何语言: ∵AD//BC,AD=BC
∴四边形ABCD是平行四边形
平行四边形的判定定理2
两组对边分别相等的四边形是平行四边形
几何语言: ∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
想一想,判定定理1和判定定理2有什么关系?
已知一组对边相等,要想证明是平行四边形,只需证明另一组对边相等或者是该组对边平行
想一想,两组对角相等的四边形是平行四边形吗?
已知:如图,在四边形ABCD中,∠A=∠C, ∠B=∠D
求证:四边形ABCD是平行四边形
证明:∵∠A=∠C,,∠B=∠D,∠A+∠B+∠C+∠D=360°
∴2∠A+2∠B=360°
∴∠A+∠B=180°
∴AD//BC
同理可证AB//CD
∴四边形ABCD是平行四边形
于是,就得到
两组对角相等的四边形是平行四边形
A
D
B
C
已知:如图,E,F,G,H分别是平行四边形ABCD的边AD,AB,BC,CD上的点,且AE=CG,BF=DH.
求证:四边形EFGH是平行四边形
证明:∵四边形ABCD是平行四边形
∴∠A=∠C,AB=CD
∵BF=DH
∴AF=CH
∵AE=CG
∴△AFE≌△CHG(ASA)
∴EF=GH
同理,FG=HE
∴四边形EFGH是平行四边形
小亮猜测:“在四边形中,能否根据一组对边相等,另一组对边平行,判断这个四边形是平行四边形呢?”
小亮的猜测正确吗?如果正确,请给出正面;如果不正确,请举出反例.
不正确,反例是等腰梯形
1.如图,在四边形ABCD中,∠ADB=∠CBD, ∠ABD=∠CDB.利用三种方法证明四边形ABCD是平行四边形。
方法一:证明:∵∠ADB=∠CBD
∴AD//BC
∵∠ABD=∠CDB
∴AB//CD
∴四边形ABCD是平行四边形
方法二:证明:∵∠ADB=∠CBD,BD=DB,∠ABD=∠CDB
∴△ABD≌△CDB(ASA)
∴AB=CD,AD=CB
∴四边形ABCD是平行四边形
方法三:证明:∵∠ADB=∠CBD,BD=DB,∠ABD=∠CDB
∴△ABD≌△CDB(ASA)
∴AB=CD,AD=CB
∵∠ABD=∠CDB
∴AB//CD
∴四边形ABCD是平行四边形
2.如图,在平行四边形ABCD中,点E,F分别是AD,BC的中点。分别利用判定定理1和判定定理2证明四边形BEDF是平行四边形。
方法一:∵四边形ABCD是平行四边形
∴AD//BC,AD=BC
∵点E,F分别是AD,BC的中点
∴DE=12????????,????????=12BC
∴DE=BF
∴四边形BEDF是平行四边形
?
方法二:∵四边形ABCD是平行四边形
∴AB=CD,AD=BC, ∠A=∠C
∵点E,F分别是AD,BC的中点
∴DE=12????????,????????=12BC
∴AE=DE=BF=CF
∴△ABE≌△CDF(SAS)
∴BE=DF
∴四边形BEDF是平行四边形
?
平行四边形的判定定理1
一组对边平行且相等的四边形是平行四边形
几何语言: ∵AD//BC,AD=BC
∴四边形ABCD是平行四边形
平行四边形的判定定理2
两组对边分别相等的四边形是平行四边形
几何语言: ∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
课本P15,复习与巩固 第1题,第2题
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
