人教版五年级下册数学第四单元第3课时 真分数和假分数 课件(23张 )
文档属性
| 名称 | 人教版五年级下册数学第四单元第3课时 真分数和假分数 课件(23张 ) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 06:55:06 | ||
图片预览







文档简介
分数的意义和性质
真分数和假分数
一、创设情境,引入新知
1. 提出问题。
(1)把3个月饼平均分给4人,每人分得多少个?
(2)把5个月饼平均分给4人,每人分得多少个?
对于这个结果,你能在圆上表示出来吗?
在这个圆上可以怎么表示出 呢?
4
3
你是怎么得到的 ?
4
5
根据分数与除法的关系得到5÷4= 。
4
5
一、创设情境,引入新知
2. 质疑:
究竟有多大呢?你能用圆把 表示出来吗?
追问:你们说不够是怎么回事?
4
5
4
5
请拿学具表示,一个圆能表示 吗?
4
5
1个圆最多表示 ,要表示 还差1个 。
4
4
4
5
4
1
每人拿出1号学具袋里的圆试试吧。
二、操作探究,理解分数的意义
( 3 )
① ②
1. 引导学生表示出“ ”。
4
5
( 1 )大家手中的一个圆无法表示 。你们能想想办法表示出它吗?
4
5
( 2 )请同桌两个人合作表示出一个 。
4
5
针对预设①研讨:你是怎么取的5份?
第一个圆平均分成4份,取了4份,再把第二个圆平均分成
4份,取1份,合在一起是5个 ,就是 。
4
5
4
1
把一个圆平均分成4份,表示这样的5份就是 。
4
5
( 4 )你觉得 表示什么意思?
4
5
二、操作探究,理解分数的意义
请动手移动。
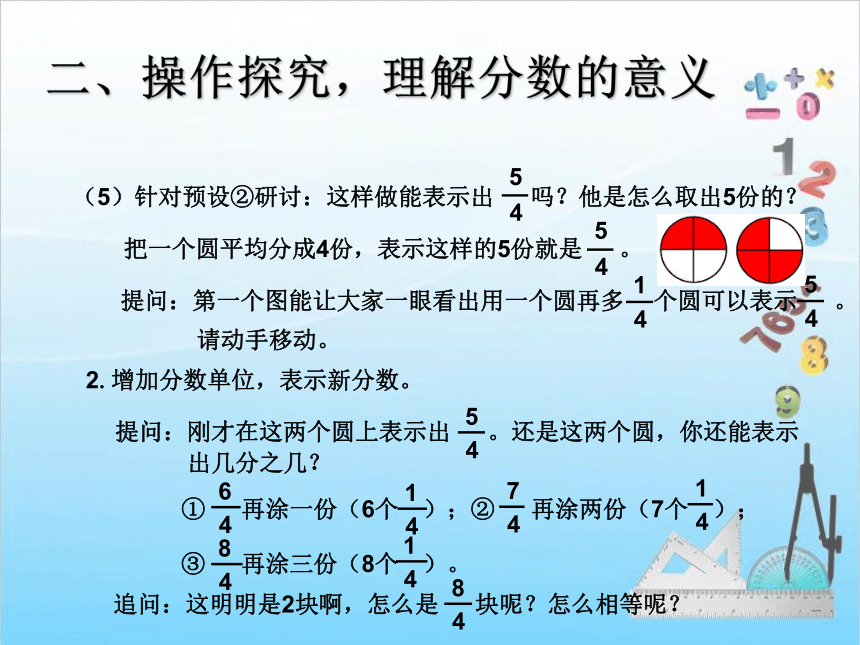
(5)针对预设②研讨:这样做能表示出 吗?他是怎么取出5份的?
4
5
把一个圆平均分成4份,表示这样的5份就是 。
4
5
提问:第一个图能让大家一眼看出用一个圆再多 个圆可以表示 。
4
1
4
5
提问:刚才在这两个圆上表示出 。还是这两个圆,你还能表示
出几分之几?
4
5
追问:这明明是2块啊,怎么是 块呢?怎么相等呢?
4
8
① 再涂一份(6个 );② 再涂两份(7个 );
③ 再涂三份(8个 )。
4
6
4
1
4
8
4
1
4
1
4
7
2.增加分数单位,表示新分数。
二、操作探究,理解分数的意义
追问:你有不同的表示方法吗?
( 2 )先在组内交流商讨一下,通过合作表示出 。
4
9
3. 借助操作表示 ,进一步理解假分数的意义。
4
9
( 1 )提问: 你都会表示了,那 呢?你能用2号学具袋中的圆
表示出 吗?
4
8
4
9
4
9
( 3 )小组合作表示 。
4
9
提问:①你是怎么取出9份的? ② 表示什么意思?
4
9
选取3个以上圆形表示 。
4
9
二、操作探究,理解分数的意义
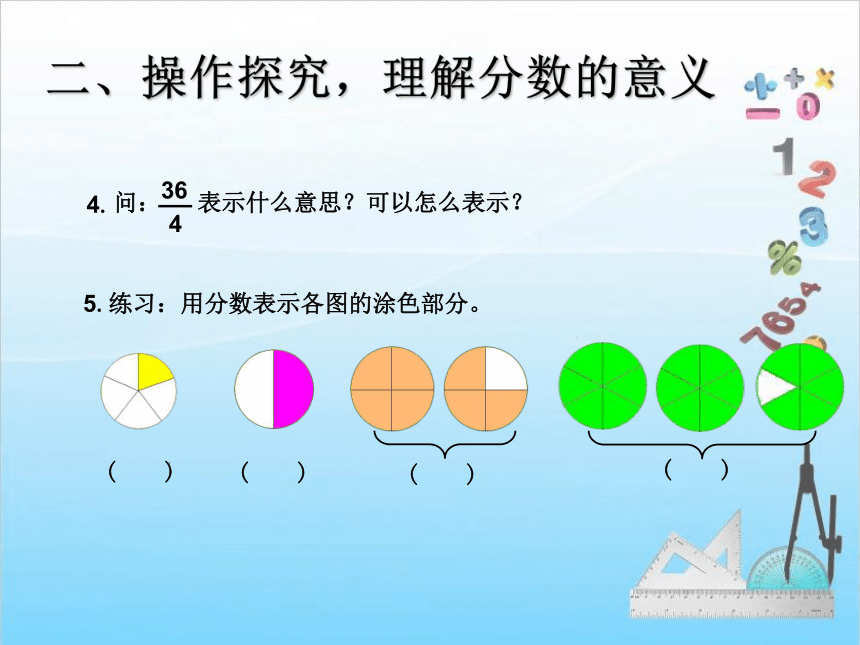
5.练习:用分数表示各图的涂色部分。
( )
( )
( )
问: 表示什么意思?可以怎么表示?
4.
4
36
( )
三、借助直线上的点表示分数,
尝试分类,揭示概念
1.如果在直线上,你还能找到这样的分数吗?
在直线上标出下列分数的位置。
(一)在直线上表示分数
2.提问:①你是怎么找到 、 的位置的?有什么好方法?
2
1
4
1
② 怎么在1的位置了?对吗?你是怎么想的?
3
3
③ 怎么想到写在1后面? 为什么会在2的后面?
4
7
5
11
0
1
2
2
1
4
1
5
2
3
3
4
7
5
11
(二)对分数进行分类
三、借助直线上的点表示分数,
尝试分类,揭示概念
1.提问:你们知道分数分为几类吗?
3.汇报。
2.请在小组内讨论分数可以分为几类。
①分成3类,根据分子与分母间大小关系。
第1类:分子<分母;第2类:分子=分母;第3类:分子>分母
②分成3类,根据分数与1间大小关系。
第1类:分数< 1;第2类:分数=1;第3类:分数> 1
③分成两类,真分数和假分数 。
三、借助直线上的点表示分数,
尝试分类,揭示概念
4.分类标准不同。
分子比分母小的分数比1小;分子与分母相等的分数就等于1;分子比分母大的分数比1大。
5.揭示真分数、假分数概念:
这里的第一类叫真分数,第二类与第三类统称为假分数。
a=b =1
b
a
a>b >1
b
a
a<b <1
b
a
三、借助直线上的点表示分数,
尝试分类,揭示概念
6. 带分数概念:
(1)
把1个圆作为单位“1”。分别涂色表示下面各假分数。
通过对圆形涂色表示出这4个假分数。你有什么发现?
① 是1个圆; ② 是1个圆多 个圆;
③ 是1个圆多 个圆; ④ 是2个圆多 个圆;
3
1
5
1
3
4
5
11
4
7
3
3
4
3
3
4
3
3
5
11
4
7
三、借助直线上的点表示分数,
尝试分类,揭示概念
(7) 提问:你能说几个带分数吗?
(4) 由涂色可以看出, 可以看做由 和 ,也就是1和 合成的数
3
4
3
3
3
1
3
1
(5) 和 能写成这样的形式吗?
4
7
5
11
(6) 小结:像1 、1 和2 ……这样由整数和真分数合成的
数叫带分数。
3
1
4
3
5
1
四、探究把假分数化为整数或
带分数的方法
2. 等于几呢? 请将你的方法和答案写在题纸上。
①根据分数与除法的关系。
3÷3=1 8÷4=2
(一)假分数化为整数
1. 例3(1):把 和 化成整数。
3
3
4
8
②根据分数的意义。
3个 是1; 8个 是2 。
3
1
4
1
=8÷4 =2。
4. 这两个结果都是什么数?你有什么发现吗?交流一下。
当分子是分母的倍数时,假分数可以化成整数。
3. 为什么8÷4=2, 就等于2呢?
这是在求 8个 里面有2个 ,每个 是1,
所以
4
8
4
1
4
4
4
4
4
8
7
6
四、探究把假分数化为整数或
带分数的方法
四、探究把假分数化为整数或
带分数的方法
不能化成整数,但可以化成带分数。
(二)假分数化为带分数
3. 这两个假分数可以怎样化为带分数。完成在题纸上,再和同学
交流一下。
2. 和 的分子是分母的倍数吗?那还能化成整数吗?
3
7
6
5
1. 例3(2):把 和 化成带分数。
6
5
3
7
根据分数与除法的关系。 =6÷5=1 ,用6÷5,所商的1
表示6 个 里面有1个 ,每个 是1,所以带分数的整数部分
是1;余数1表示还剩1个, 所以带分数的分数部分是 。因此,
=6÷5=1 。
5
6
5
1
5
1
5
5
5
5
5
5
5
1
5
6
5
1
根据分数与除法的关系。 =7÷3=2 ,7÷3=2……1,商2
表示7个 里面有2个 ,每个 是1,所以带分数的整数部分是
2;余数1表示还剩1个 ,所以带分数的分数部分是 。因此,
=7÷3=2 。
3
7
3
1
3
1
3
3
3
3
3
1
3
1
3
7
3
1
四、探究把假分数化为整数或
带分数的方法
﹦6÷5=1
5
6
5
1
4. 汇报:
=7÷3=2
3
7
3
1
四、探究把假分数化为整数或
带分数的方法
现在你可以用自己的话说一说把假分数化成整数或带分数
的方法吗?
(三)总结把假分数化为整数或带分数的方法
①当假分数的分子是分母的倍数时,这个假分数可以化成整数。
用分子除以分母,所得的商就是这个假分数所化成的整数。
②当假分数的分子不是分母倍数时,这个假分数可以化成带分
数。用分子除以分母,所得的商是带分数的整数部分,余数
是带分数分数部分的分子,分母不变。
用分数表示下面除法算式的商,是假分数的化成带分数。
18÷17= 17÷18=
27÷28= 101÷25=
五、综合应用,巩固理解
1.
2. 解决问题。
这板药能吃多少天?(用带分数表示出来。)
17
18
=1
17
1
18
17
28
27
25
101
=4
25
1
10÷3=
3
10
3
1
=3
(天)
4
7
( )
( )
六、巩固练习,深化理解
2. 教材第54页“做一做”,第1题。
1. 教材第55页,第1题。
把一个图形看作单位“1”,用分数表示出各图涂色部分的大小,再读一读。
6
23
下面的分数中哪些是真分数?哪些是假分数?在直线上表示出来。
0
2
1
3
1
3
3
3
5
6
1
6
5
6
7
6
13
看一看,表示真分数的点和表示假分数的点,分别在直线的哪一段上。
6
13
3
3
6
7
3
5
七、课堂总结
通过这节课的学习,你有哪些新的收获呀?
第55页练习十三,第3题、第4题、第5题。
八、作业布置
真分数和假分数
一、创设情境,引入新知
1. 提出问题。
(1)把3个月饼平均分给4人,每人分得多少个?
(2)把5个月饼平均分给4人,每人分得多少个?
对于这个结果,你能在圆上表示出来吗?
在这个圆上可以怎么表示出 呢?
4
3
你是怎么得到的 ?
4
5
根据分数与除法的关系得到5÷4= 。
4
5
一、创设情境,引入新知
2. 质疑:
究竟有多大呢?你能用圆把 表示出来吗?
追问:你们说不够是怎么回事?
4
5
4
5
请拿学具表示,一个圆能表示 吗?
4
5
1个圆最多表示 ,要表示 还差1个 。
4
4
4
5
4
1
每人拿出1号学具袋里的圆试试吧。
二、操作探究,理解分数的意义
( 3 )
① ②
1. 引导学生表示出“ ”。
4
5
( 1 )大家手中的一个圆无法表示 。你们能想想办法表示出它吗?
4
5
( 2 )请同桌两个人合作表示出一个 。
4
5
针对预设①研讨:你是怎么取的5份?
第一个圆平均分成4份,取了4份,再把第二个圆平均分成
4份,取1份,合在一起是5个 ,就是 。
4
5
4
1
把一个圆平均分成4份,表示这样的5份就是 。
4
5
( 4 )你觉得 表示什么意思?
4
5
二、操作探究,理解分数的意义
请动手移动。
(5)针对预设②研讨:这样做能表示出 吗?他是怎么取出5份的?
4
5
把一个圆平均分成4份,表示这样的5份就是 。
4
5
提问:第一个图能让大家一眼看出用一个圆再多 个圆可以表示 。
4
1
4
5
提问:刚才在这两个圆上表示出 。还是这两个圆,你还能表示
出几分之几?
4
5
追问:这明明是2块啊,怎么是 块呢?怎么相等呢?
4
8
① 再涂一份(6个 );② 再涂两份(7个 );
③ 再涂三份(8个 )。
4
6
4
1
4
8
4
1
4
1
4
7
2.增加分数单位,表示新分数。
二、操作探究,理解分数的意义
追问:你有不同的表示方法吗?
( 2 )先在组内交流商讨一下,通过合作表示出 。
4
9
3. 借助操作表示 ,进一步理解假分数的意义。
4
9
( 1 )提问: 你都会表示了,那 呢?你能用2号学具袋中的圆
表示出 吗?
4
8
4
9
4
9
( 3 )小组合作表示 。
4
9
提问:①你是怎么取出9份的? ② 表示什么意思?
4
9
选取3个以上圆形表示 。
4
9
二、操作探究,理解分数的意义
5.练习:用分数表示各图的涂色部分。
( )
( )
( )
问: 表示什么意思?可以怎么表示?
4.
4
36
( )
三、借助直线上的点表示分数,
尝试分类,揭示概念
1.如果在直线上,你还能找到这样的分数吗?
在直线上标出下列分数的位置。
(一)在直线上表示分数
2.提问:①你是怎么找到 、 的位置的?有什么好方法?
2
1
4
1
② 怎么在1的位置了?对吗?你是怎么想的?
3
3
③ 怎么想到写在1后面? 为什么会在2的后面?
4
7
5
11
0
1
2
2
1
4
1
5
2
3
3
4
7
5
11
(二)对分数进行分类
三、借助直线上的点表示分数,
尝试分类,揭示概念
1.提问:你们知道分数分为几类吗?
3.汇报。
2.请在小组内讨论分数可以分为几类。
①分成3类,根据分子与分母间大小关系。
第1类:分子<分母;第2类:分子=分母;第3类:分子>分母
②分成3类,根据分数与1间大小关系。
第1类:分数< 1;第2类:分数=1;第3类:分数> 1
③分成两类,真分数和假分数 。
三、借助直线上的点表示分数,
尝试分类,揭示概念
4.分类标准不同。
分子比分母小的分数比1小;分子与分母相等的分数就等于1;分子比分母大的分数比1大。
5.揭示真分数、假分数概念:
这里的第一类叫真分数,第二类与第三类统称为假分数。
a=b =1
b
a
a>b >1
b
a
a<b <1
b
a
三、借助直线上的点表示分数,
尝试分类,揭示概念
6. 带分数概念:
(1)
把1个圆作为单位“1”。分别涂色表示下面各假分数。
通过对圆形涂色表示出这4个假分数。你有什么发现?
① 是1个圆; ② 是1个圆多 个圆;
③ 是1个圆多 个圆; ④ 是2个圆多 个圆;
3
1
5
1
3
4
5
11
4
7
3
3
4
3
3
4
3
3
5
11
4
7
三、借助直线上的点表示分数,
尝试分类,揭示概念
(7) 提问:你能说几个带分数吗?
(4) 由涂色可以看出, 可以看做由 和 ,也就是1和 合成的数
3
4
3
3
3
1
3
1
(5) 和 能写成这样的形式吗?
4
7
5
11
(6) 小结:像1 、1 和2 ……这样由整数和真分数合成的
数叫带分数。
3
1
4
3
5
1
四、探究把假分数化为整数或
带分数的方法
2. 等于几呢? 请将你的方法和答案写在题纸上。
①根据分数与除法的关系。
3÷3=1 8÷4=2
(一)假分数化为整数
1. 例3(1):把 和 化成整数。
3
3
4
8
②根据分数的意义。
3个 是1; 8个 是2 。
3
1
4
1
=8÷4 =2。
4. 这两个结果都是什么数?你有什么发现吗?交流一下。
当分子是分母的倍数时,假分数可以化成整数。
3. 为什么8÷4=2, 就等于2呢?
这是在求 8个 里面有2个 ,每个 是1,
所以
4
8
4
1
4
4
4
4
4
8
7
6
四、探究把假分数化为整数或
带分数的方法
四、探究把假分数化为整数或
带分数的方法
不能化成整数,但可以化成带分数。
(二)假分数化为带分数
3. 这两个假分数可以怎样化为带分数。完成在题纸上,再和同学
交流一下。
2. 和 的分子是分母的倍数吗?那还能化成整数吗?
3
7
6
5
1. 例3(2):把 和 化成带分数。
6
5
3
7
根据分数与除法的关系。 =6÷5=1 ,用6÷5,所商的1
表示6 个 里面有1个 ,每个 是1,所以带分数的整数部分
是1;余数1表示还剩1个, 所以带分数的分数部分是 。因此,
=6÷5=1 。
5
6
5
1
5
1
5
5
5
5
5
5
5
1
5
6
5
1
根据分数与除法的关系。 =7÷3=2 ,7÷3=2……1,商2
表示7个 里面有2个 ,每个 是1,所以带分数的整数部分是
2;余数1表示还剩1个 ,所以带分数的分数部分是 。因此,
=7÷3=2 。
3
7
3
1
3
1
3
3
3
3
3
1
3
1
3
7
3
1
四、探究把假分数化为整数或
带分数的方法
﹦6÷5=1
5
6
5
1
4. 汇报:
=7÷3=2
3
7
3
1
四、探究把假分数化为整数或
带分数的方法
现在你可以用自己的话说一说把假分数化成整数或带分数
的方法吗?
(三)总结把假分数化为整数或带分数的方法
①当假分数的分子是分母的倍数时,这个假分数可以化成整数。
用分子除以分母,所得的商就是这个假分数所化成的整数。
②当假分数的分子不是分母倍数时,这个假分数可以化成带分
数。用分子除以分母,所得的商是带分数的整数部分,余数
是带分数分数部分的分子,分母不变。
用分数表示下面除法算式的商,是假分数的化成带分数。
18÷17= 17÷18=
27÷28= 101÷25=
五、综合应用,巩固理解
1.
2. 解决问题。
这板药能吃多少天?(用带分数表示出来。)
17
18
=1
17
1
18
17
28
27
25
101
=4
25
1
10÷3=
3
10
3
1
=3
(天)
4
7
( )
( )
六、巩固练习,深化理解
2. 教材第54页“做一做”,第1题。
1. 教材第55页,第1题。
把一个图形看作单位“1”,用分数表示出各图涂色部分的大小,再读一读。
6
23
下面的分数中哪些是真分数?哪些是假分数?在直线上表示出来。
0
2
1
3
1
3
3
3
5
6
1
6
5
6
7
6
13
看一看,表示真分数的点和表示假分数的点,分别在直线的哪一段上。
6
13
3
3
6
7
3
5
七、课堂总结
通过这节课的学习,你有哪些新的收获呀?
第55页练习十三,第3题、第4题、第5题。
八、作业布置
