利用导数研究函数的极值

§1.3.2利用导数研究函数的极值 学案 05.08
一、学习目标
知识与技能：理解极大值、极小值的概念； 能够运用判别极大值、极小值的方法来求函数的极值； 掌握求可导函数的极值的步骤；
过程与方法：多让学生举命题的例子，培养他们的辨析能力；以及培养他们的分析问题和解决问题的能力；
情感、态度与价值观：通过学生的参与，激发学生学习数学的兴趣。
二、学习重点与难点
教学重点：极大、极小值的概念和判别方法，以及求可导函数的极值的步骤.
教学难点：对极大、极小值概念的理解及求可导函数的极值的步骤.
三、学习过程：
（一）复习提问
利用导数判断函数单调性的法则:
解不等式>0得f(x)的单调递增区间;
解不等式<0得f(x)的单调递减区间.
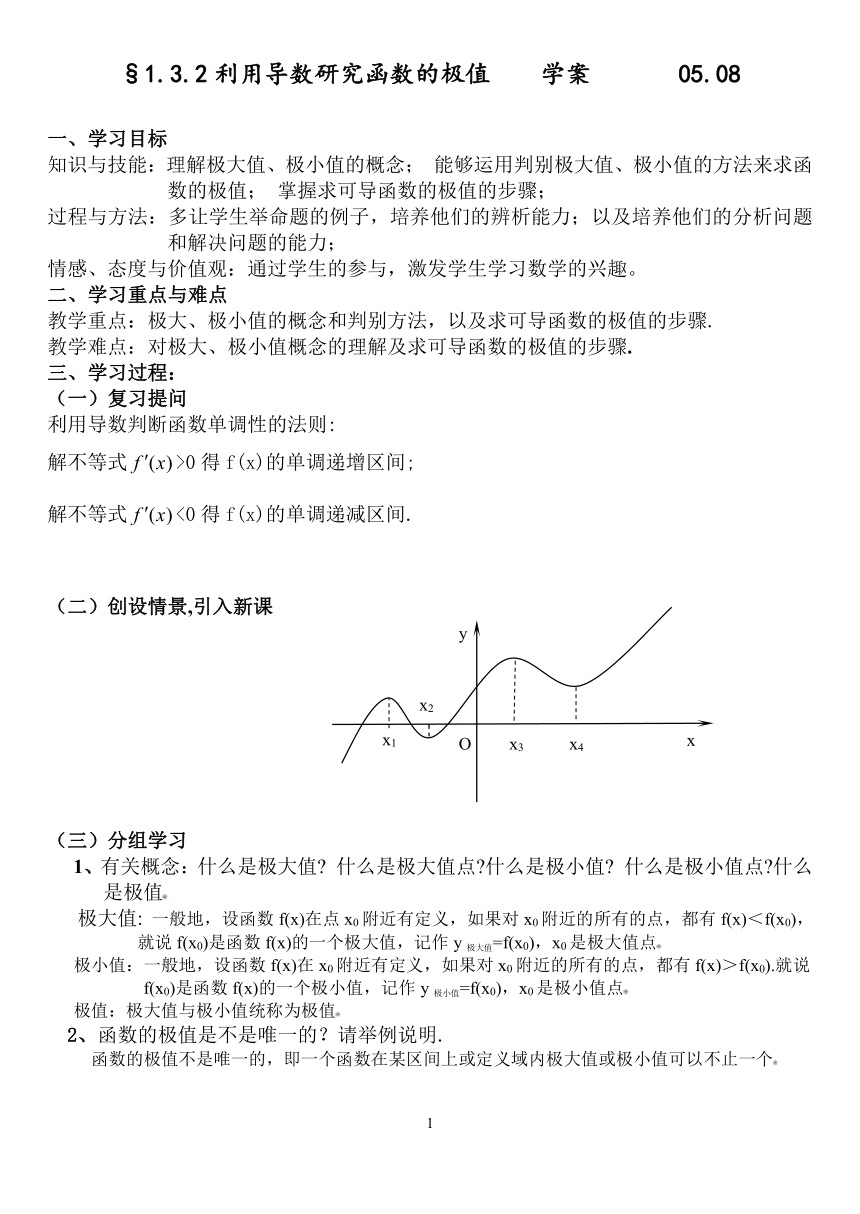
（二）创设情景,引入新课
（三）分组学习
1、有关概念：什么是极大值 什么是极大值点 什么是极小值 什么是极小值点 什么是极值
极大值: 一般地，设函数f(x)在点x0附近有定义，如果对x0附近的所有的点，都有f(x)＜f(x0)，就说f(x0)是函数f(x)的一个极大值，记作y极大值=f(x0)，x0是极大值点
极小值：一般地，设函数f(x)在x0附近有定义，如果对x0附近的所有的点，都有f(x)＞f(x0).就说f(x0)是函数f(x)的一个极小值，记作y极小值=f(x0)，x0是极小值点
极值：极大值与极小值统称为极值
2、函数的极值是不是唯一的？请举例说明.
函数的极值不是唯一的，即一个函数在某区间上或定义域内极大值或极小值可以不止一个
3、极大值与极小值之间有无确定的大小关系 请举例说明.
极大值与极小值之间无确定的大小关系。即一个函数的极大值未必大于极小值，如上图所示， 是极大值点，是极小值点，而>
4、极大值一定比极小值大吗？请举例说明.
极大值不一定比极小值大，极大值与极小值没有必然的大小关系
5、点是极值点是在该点的导数为0的什么条件？请举例说明
可导函数f(x),点是极值点是在该点的导数为0的必要条件. 例：y=x3
6、极值一定是最大值或最小值吗？请举例说明.
极值不一定是最大值或最小值.
（四）典例分析
例1、求函数的极值.
解:=3(x+3)(x－3)，
令解得
当x 变化时,、的变化情况如下表:
x (-∞,-3) -3 (-3,3) 3 (3,+∞)
+ 0 - 0 +
↗ 极大值54 ↘ 极小值-54 ↗
因此,当x=-3时有极大值,并且, y极大值=54;
当x=3时有极小值,并且, y极小值=-54.
例2、已知函数.
（1）求函数的极值，并画出函数的大致图象；
（2）求函数在区间[－3，4]上的最大值和最小值.
解:（1）
令,解得x1=-2,x2=2.
当x变化时,、的变化情况如下表：
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
+ 0 - 0 +
↗ 极大值28/3 ↘ 极小值-4/3 ↗
因此,当x=-2时有极大值,并且,y极大值=28/3;
当x=2时有极小值,并且,y极小值=- 4/3.
（2）
例3、已知函数f(x)=x3+ax2+bx+a2在x=1处有极值为10,求a、b的值.
解: =3x2+2ax+b=0有一个根x=1,故3+2a+b=0.①
又f(1)=10,故1+a+b+a2=10.②
由①、②解得或
当a=-3,b=3时,,此时f(x)在x=1处无极值,不合题意.
当a=4,b=-11时,
-11/31时,,此时x=1是极值点.
从而所求的解为a=4,b=-11.
例3、已知函数f(x)=-x3+ax2+b.若函数f(x)在x=0,x=4处取得极值,且极小值为-1,
求a、b的值.
解:(1)由得x=0或x=2a/3.故2a/3=4,a=6.
由于当x<0时,当x>0时,故当x=0时,f(x)达到极小值f(0)=b,所以b=-1.
五．回顾总结
求函数极值的一般步骤：
（1）求导数
（2）解方程=0，利用方程的根x0，顺次将函数的定义域分成若干个开区间，并列成表格
（3）由在方程=0的根左右的符号，来判断f(x)在这个根处取极值的情况:
① 若f’(x)在x0两侧的符号“左正右负”，则x0 为极大值点;
② 若f’(x)在x0两侧的符号“左负右正”，则x0 为极小值点;
③ 若f’(x)在x0两侧的符号相同，则x0 不是极值点.
(1) 导数为零的点不一定是极值点！
(2)函数的极值是就函数在某一点附近的小区间而言的,在函数的整个定义域可能有多个极大值或极小值, 不唯一!
(3) 极大值不一定比极小值大!
(4)函数的不可导点也可能是极值点;
(5)可导函数的极值点一定是使导函数为0的点.
x2
x
y
O
x1
x3
x4
PAGE
2