人教版数学五年级下册 第四单元 最小公倍数的应用 课件(37张ppt)
文档属性
| 名称 | 人教版数学五年级下册 第四单元 最小公倍数的应用 课件(37张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 08:49:13 | ||
图片预览










文档简介
最小公倍数的应用
人教版数学五年级下册 第四单元
学习目标
1.加深对公倍数和最小公倍数意义的理解,探究用求最小公倍数解决实际问题的方法。
2.经历探究过程,感知公倍数和最小公倍数在生活中的广泛应用。
3.感受数形结合思想,培养独立思考的能力。
复习
1.什么叫公倍数和最小公倍数?
两个数公有的倍数,叫做它们的公倍数;其中最小的公倍数叫做它们的最小公倍数。
6,12,18,24,30,36,42···
4,8,12,16,20,24,28,32,36,40···
4的倍数
6的倍数
12
12
24
36
24
36
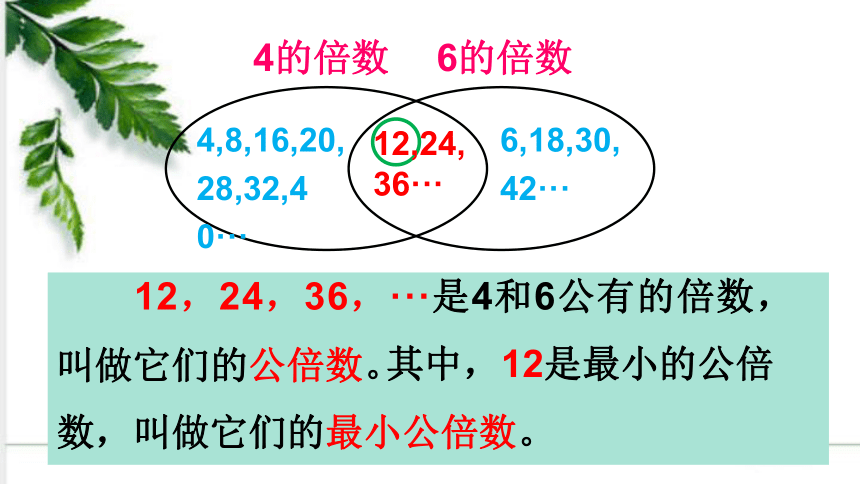
12,24,36,···是4和6公有的倍数,叫做它们的公倍数。
其中,12是最小的公倍数,叫做它们的最小公倍数。
4的倍数
6的倍数
4,8,16,20,28,32,40···
6,18,30,42···
12,24,36···
2.怎样求两个数的公倍数和最小公倍数?
①列举法,先分别列出两个数各自的倍数,再圈出它们的公倍数和最小公倍数。
4的倍数:4,8,12,16,20,24,28,32,36,40···
6的倍数:6,12,18,24,30,36,42···
4和6的公倍数有 12,24,36···
4和6的最小公倍数是 12。
列举法
②筛选法,先列出较大数的倍数,再从中圈出另一个数的倍数,就是它们的公倍数;公倍数中最小的数就是它们的最小公倍数。
2.怎样求两个数的公倍数和最小公倍数?
筛选法
4和6的公倍数有 12,24,36···
6的倍数:6,12,18,24,30,36,42···
4和6的最小公倍数是 12。
分解质因数法和短除法。
3.求较大的两个数最小公倍数的简便方法。
这节课我们利用两个数的最小公倍数来解决生活中的数学问题。
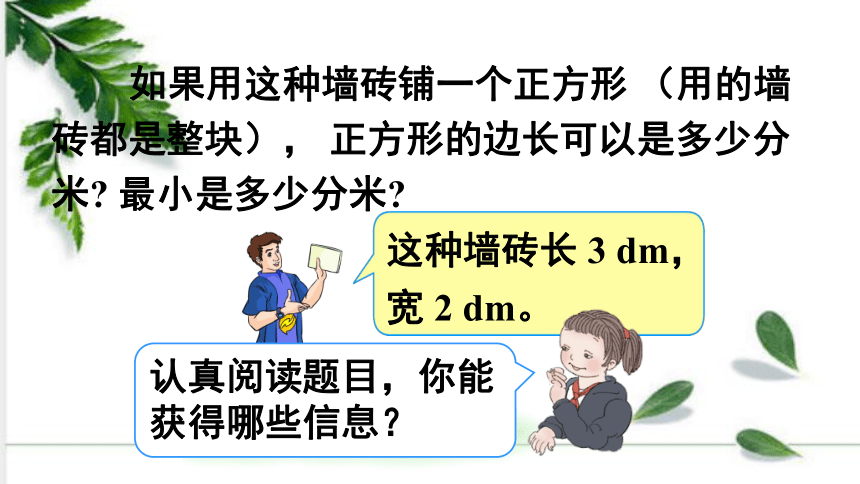
这种墙砖长 3 dm,宽 2 dm。
如果用这种墙砖铺一个正方形 (用的墙砖都是整块), 正方形的边长可以是多少分米? 最小是多少分米?
认真阅读题目,你能获得哪些信息?
墙砖长 3 dm,宽 2 dm。
用这种墙砖铺一个正方形 (用的墙砖都是整块), 正方形的边长可以是多少分米? 最小是多少分米?
阅读与理解
01
要满足用整块的这种长方形墙砖铺出一个正方形,正方形的边长必须符合什么条件?
3dm
2dm
用长是3dm,宽是2dm的长方形来拼一拼。
我们先来研究正方形的边长可以是多少分米。你有办法解决这个问题吗?
要用整块的这种长方形墙砖铺出一个正方形。
铺成的正方形可能很多种。
3dm
2dm
?dm
?dm
分析与解答
02
第一行沿着长方形的长边摆2个长方形,长度为6dm,第一列沿着长方形的宽边摆3个长方形,长度为6dm,拼成一个边长是6dm的正方形。
3dm
2dm
3dm
6dm
6dm
12dm
3dm
2dm
你还能拼成不一样的大正方形吗?动手画一画。
第一行沿着长方形的长边摆4个长方形,长度为12dm,第一列沿着长方形的宽边摆6个长方形,长度为12dm,拼成一个边长是12dm的正方形。
12dm
用整块的长3dm,宽2dm的长方形墙砖铺出一个正方形,正方形的边长必须既是 3 的倍数,又是 2 的倍数。
只要找出2和3的公倍数和最小公倍数,就能知道所铺的正方形的边长和最小边长。
2的倍数有:2,4,6,8,10,12,14,16,18,···
3的倍数有:3,6,9,12,15,18,···
2和3的公倍数有:
6,12,18,···
3的倍数有:3,6,9,12,15,18,···
所以,铺成的正方形的边长可以是6dm,12dm,18dm···
正方形边长最小是 。
2和3的最小公倍数是:6
6dm
画一画,算一算。
回顾与反思
03
3dm
2dm
18÷3=6(个)第一行沿着长方形的长边摆,摆了6个长方形;
18dm
18÷2=9(个)第一列沿着长方形的宽边摆,摆了9个长方形;
说明边长为18dm的正方形恰好用整块的长方形墙砖铺满。
解决这个问题的关键是把铺砖问题转化成求公倍数和最小公倍数的问题。
答:正方形的边长可以是6分米,12分米,18分米…;最小是6分米。
回顾与反思
03
实际问题
数学问题
转化
1. 李阿姨5月1日给月季和君子兰同时浇了水,下一次再给这两种花同时浇水应是5月几日?
月季每 4 天浇一次水,君
子兰每 6 天浇一次水。
同时浇水
浇月季花
浇君子兰
(每4天)
(每6天)
下一次再给这两种花同时浇水应是5月13日。
发现:13-1=12(天),
12是4和6的最小公倍数。
同时浇水
浇昙花
浇杜鹃花
(每6天)
(每9天)
下一次再给这两种花同时浇水应是5月20日。
发现:20-2=18(天),
18是6和9的最小公倍数。
4的倍数有:4,8,12,16,20,24,28,···
6的倍数有:6,12,18,24,30,···
4和6的公倍数有:12,24,···
4和6的最小公倍数是12。
1+12=13(日)
答:下一次再给这两种花同时浇水应该是5月13日。
如果这些学生的总人数在40人以内,可能是多少人?
咱们可以分成6人一组,也可以分成9人一组,都正好分完。
2.
求40以内6和9的公倍数。
咱们可以分成6人一组,也可以分成9人一组,都正好分成。
2.
答:如果这些学生的总人数在40人以内,可能是18人或36人。
9的倍数有:9,18,27,36,···
6和9的公倍数有:18,36,···
如果爸爸妈妈同时起跑,至少多少分钟后两人在起点再次相遇? 此时爸爸,妈妈分别跑了多少圈?
我跑一圈用
3 分钟。
我跑一圈用 4 分钟。
我要用
6 分钟。
3.
4的倍数有:4,8,12,16,20,24,···
3和4的公倍数有:12,24,···
爸爸:12÷3=4(圈)
答:至少12分钟后两人在起点再次相遇。
妈妈:12÷4=3(圈)
3和4的最小公倍数是:12。
答:此时爸爸跑了4圈,妈妈跑了3圈。
你还能提出什么问题吗?
三人同时起跑,至少多少分钟后三人在起点再次相遇?
求多少分钟后三人在起点相遇,就是求3,4和6的最小公倍数。
3的倍数有:3,6,9,12,15,18,21,24,…
4的倍数有:4,8,12,16,20,24,…
6的倍数有:6,12,18,24,…
3,4,6的公倍数有12,24,…
3,4,6的最小公倍数为12。
也就是三人同时起跑,至少12分钟后三人在起点相遇。
答:至少12分钟后三人在起点再次相遇。
4.用长6cm,宽4cm,高3cm的长方体木块摆成一个正方体,至少要用这样的木块多少块?
6,4,3的最小公倍数是12。
答:至少要用这样的木块24块。
6的倍数有:6,12,18,24,30,···
(12×12×12)÷(6×4×3)=24(块)
今天你有什么收获呢?
学习目标
1.加深对公倍数和最小公倍数意义的理解,探究用求最小公倍数解决实际问题的方法。
2.经历探究过程,感知公倍数和最小公倍数在生活中的广泛应用。
3.感受数形结合思想,培养独立思考的能力。
再见!
人教版数学五年级下册 第四单元
学习目标
1.加深对公倍数和最小公倍数意义的理解,探究用求最小公倍数解决实际问题的方法。
2.经历探究过程,感知公倍数和最小公倍数在生活中的广泛应用。
3.感受数形结合思想,培养独立思考的能力。
复习
1.什么叫公倍数和最小公倍数?
两个数公有的倍数,叫做它们的公倍数;其中最小的公倍数叫做它们的最小公倍数。
6,12,18,24,30,36,42···
4,8,12,16,20,24,28,32,36,40···
4的倍数
6的倍数
12
12
24
36
24
36
12,24,36,···是4和6公有的倍数,叫做它们的公倍数。
其中,12是最小的公倍数,叫做它们的最小公倍数。
4的倍数
6的倍数
4,8,16,20,28,32,40···
6,18,30,42···
12,24,36···
2.怎样求两个数的公倍数和最小公倍数?
①列举法,先分别列出两个数各自的倍数,再圈出它们的公倍数和最小公倍数。
4的倍数:4,8,12,16,20,24,28,32,36,40···
6的倍数:6,12,18,24,30,36,42···
4和6的公倍数有 12,24,36···
4和6的最小公倍数是 12。
列举法
②筛选法,先列出较大数的倍数,再从中圈出另一个数的倍数,就是它们的公倍数;公倍数中最小的数就是它们的最小公倍数。
2.怎样求两个数的公倍数和最小公倍数?
筛选法
4和6的公倍数有 12,24,36···
6的倍数:6,12,18,24,30,36,42···
4和6的最小公倍数是 12。
分解质因数法和短除法。
3.求较大的两个数最小公倍数的简便方法。
这节课我们利用两个数的最小公倍数来解决生活中的数学问题。
这种墙砖长 3 dm,宽 2 dm。
如果用这种墙砖铺一个正方形 (用的墙砖都是整块), 正方形的边长可以是多少分米? 最小是多少分米?
认真阅读题目,你能获得哪些信息?
墙砖长 3 dm,宽 2 dm。
用这种墙砖铺一个正方形 (用的墙砖都是整块), 正方形的边长可以是多少分米? 最小是多少分米?
阅读与理解
01
要满足用整块的这种长方形墙砖铺出一个正方形,正方形的边长必须符合什么条件?
3dm
2dm
用长是3dm,宽是2dm的长方形来拼一拼。
我们先来研究正方形的边长可以是多少分米。你有办法解决这个问题吗?
要用整块的这种长方形墙砖铺出一个正方形。
铺成的正方形可能很多种。
3dm
2dm
?dm
?dm
分析与解答
02
第一行沿着长方形的长边摆2个长方形,长度为6dm,第一列沿着长方形的宽边摆3个长方形,长度为6dm,拼成一个边长是6dm的正方形。
3dm
2dm
3dm
6dm
6dm
12dm
3dm
2dm
你还能拼成不一样的大正方形吗?动手画一画。
第一行沿着长方形的长边摆4个长方形,长度为12dm,第一列沿着长方形的宽边摆6个长方形,长度为12dm,拼成一个边长是12dm的正方形。
12dm
用整块的长3dm,宽2dm的长方形墙砖铺出一个正方形,正方形的边长必须既是 3 的倍数,又是 2 的倍数。
只要找出2和3的公倍数和最小公倍数,就能知道所铺的正方形的边长和最小边长。
2的倍数有:2,4,6,8,10,12,14,16,18,···
3的倍数有:3,6,9,12,15,18,···
2和3的公倍数有:
6,12,18,···
3的倍数有:3,6,9,12,15,18,···
所以,铺成的正方形的边长可以是6dm,12dm,18dm···
正方形边长最小是 。
2和3的最小公倍数是:6
6dm
画一画,算一算。
回顾与反思
03
3dm
2dm
18÷3=6(个)第一行沿着长方形的长边摆,摆了6个长方形;
18dm
18÷2=9(个)第一列沿着长方形的宽边摆,摆了9个长方形;
说明边长为18dm的正方形恰好用整块的长方形墙砖铺满。
解决这个问题的关键是把铺砖问题转化成求公倍数和最小公倍数的问题。
答:正方形的边长可以是6分米,12分米,18分米…;最小是6分米。
回顾与反思
03
实际问题
数学问题
转化
1. 李阿姨5月1日给月季和君子兰同时浇了水,下一次再给这两种花同时浇水应是5月几日?
月季每 4 天浇一次水,君
子兰每 6 天浇一次水。
同时浇水
浇月季花
浇君子兰
(每4天)
(每6天)
下一次再给这两种花同时浇水应是5月13日。
发现:13-1=12(天),
12是4和6的最小公倍数。
同时浇水
浇昙花
浇杜鹃花
(每6天)
(每9天)
下一次再给这两种花同时浇水应是5月20日。
发现:20-2=18(天),
18是6和9的最小公倍数。
4的倍数有:4,8,12,16,20,24,28,···
6的倍数有:6,12,18,24,30,···
4和6的公倍数有:12,24,···
4和6的最小公倍数是12。
1+12=13(日)
答:下一次再给这两种花同时浇水应该是5月13日。
如果这些学生的总人数在40人以内,可能是多少人?
咱们可以分成6人一组,也可以分成9人一组,都正好分完。
2.
求40以内6和9的公倍数。
咱们可以分成6人一组,也可以分成9人一组,都正好分成。
2.
答:如果这些学生的总人数在40人以内,可能是18人或36人。
9的倍数有:9,18,27,36,···
6和9的公倍数有:18,36,···
如果爸爸妈妈同时起跑,至少多少分钟后两人在起点再次相遇? 此时爸爸,妈妈分别跑了多少圈?
我跑一圈用
3 分钟。
我跑一圈用 4 分钟。
我要用
6 分钟。
3.
4的倍数有:4,8,12,16,20,24,···
3和4的公倍数有:12,24,···
爸爸:12÷3=4(圈)
答:至少12分钟后两人在起点再次相遇。
妈妈:12÷4=3(圈)
3和4的最小公倍数是:12。
答:此时爸爸跑了4圈,妈妈跑了3圈。
你还能提出什么问题吗?
三人同时起跑,至少多少分钟后三人在起点再次相遇?
求多少分钟后三人在起点相遇,就是求3,4和6的最小公倍数。
3的倍数有:3,6,9,12,15,18,21,24,…
4的倍数有:4,8,12,16,20,24,…
6的倍数有:6,12,18,24,…
3,4,6的公倍数有12,24,…
3,4,6的最小公倍数为12。
也就是三人同时起跑,至少12分钟后三人在起点相遇。
答:至少12分钟后三人在起点再次相遇。
4.用长6cm,宽4cm,高3cm的长方体木块摆成一个正方体,至少要用这样的木块多少块?
6,4,3的最小公倍数是12。
答:至少要用这样的木块24块。
6的倍数有:6,12,18,24,30,···
(12×12×12)÷(6×4×3)=24(块)
今天你有什么收获呢?
学习目标
1.加深对公倍数和最小公倍数意义的理解,探究用求最小公倍数解决实际问题的方法。
2.经历探究过程,感知公倍数和最小公倍数在生活中的广泛应用。
3.感受数形结合思想,培养独立思考的能力。
再见!
