人教版数学五年级下册 第四单元 最大公因数的应用 例3 课件(24张ppt)
文档属性
| 名称 | 人教版数学五年级下册 第四单元 最大公因数的应用 例3 课件(24张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 08:50:39 | ||
图片预览








文档简介
最大公因数的应用
人教版数学五年级下册 第四单元
1.加深对公因数和最大公因数意义的理解,探
究用求最大公因数解决实际问题的方法。
2.经历探究过程,感知公因数和最大公因数在
生活中的广泛应用。
3.感受数形结合思想,培养独立思考的能力。
学习目标:
复习
1.什么叫公因数和最大公因数?
1,2,3,4,6,12
1,2,
4,8
1,2
4
1,2,
4
8的因数
12的因数
3,
6,12
8
1,2,4
1,2,
4,
8的因数
12的因数
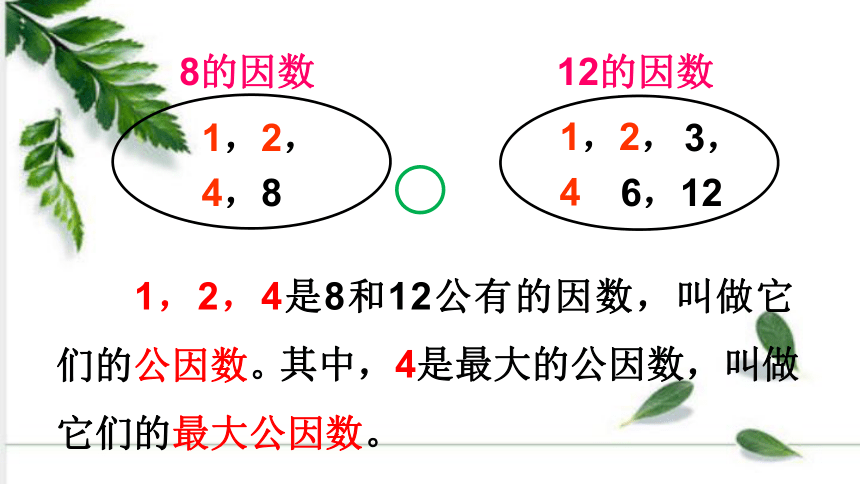
1,2,4是8和12公有的因数,叫做它们的公因数。
其中,4是最大的公因数,叫做它们的最大公因数。
2.怎样求两个数的公因数和最大公因数?
18的因数:1,2,3,6,9,18。
27的因数:1,3,9,27。
18和27的公因数是 1,3,9。其中9最大,即18和27的最大的公因数是 9。
列举法
2.怎样求两个数的公因数和最大公因数?
18的因数:1,2,3,6,9,18。
筛选法
18和27的公因数是 1,3,9
18和27的最大公因数是 9。
如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块),可以选择边长是几分米的地砖?边长最大是几分米?
16dm
12dm
边长?dm
......
地砖的边长必须是12的因数。
......
......
......
......
......
......
......
地砖的边长应符合什么条件?
地砖的边长必须是16的因数。
......
16dm
12dm
......
画一画、
算一算
......
地砖的边长是16和12的公因数。
16的因数有 1, 2, 4, 8, 16。
12的因数有 1, 2, 3, 4,6,12。
16和12的公因数:
边长最大是 。
16的因数有 1, 2, 4, 8, 16。
答:可以选边长是1dm、2dm、4dm的地砖,边长最大是4dm。
16dm
12dm
边长=1dm
16dm
12dm
边长=2dm
16dm
12dm
边长=4dm
1.有一张长方形纸,长70cm,宽50cm。如果要剪成若干同样大小的正方形纸片而没有剩余,剪出的正方形纸片的边长最大是几厘米?
2.有两根小棒,长分别是14厘米,21厘米,要把它们截成同样长的小棒,没有剩余,每根小棒最长有多少厘米?
3.男、女生分别站成若干排,要使每排的人数相同,每排最多有多少人?这时男、女生分别有几排?
女生有36人。
男生有48人。
48÷12=4(排)
36÷12=3(排)
4.将一个长30厘米、宽24厘米、高18厘米的长方体木块锯成体积相等的小正方体木块,不能有剩余,那么小正方体的棱长最大是多少?能锯成多少块这样的小正方体?
5.给一面高27分米、长36分米的卧室墙面贴壁纸,要保证用整张的壁纸不能重叠且整好贴满,可以选择下列哪几种规格的壁纸?(单位:分米)
3
3
①
6
6
②
9
9
③
3
4
④
6
9
⑤
×
√
√
√
√
36÷4=9
27÷3=9
今天你有哪些收获?
人教版数学五年级下册 第四单元
1.加深对公因数和最大公因数意义的理解,探
究用求最大公因数解决实际问题的方法。
2.经历探究过程,感知公因数和最大公因数在
生活中的广泛应用。
3.感受数形结合思想,培养独立思考的能力。
学习目标:
复习
1.什么叫公因数和最大公因数?
1,2,3,4,6,12
1,2,
4,8
1,2
4
1,2,
4
8的因数
12的因数
3,
6,12
8
1,2,4
1,2,
4,
8的因数
12的因数
1,2,4是8和12公有的因数,叫做它们的公因数。
其中,4是最大的公因数,叫做它们的最大公因数。
2.怎样求两个数的公因数和最大公因数?
18的因数:1,2,3,6,9,18。
27的因数:1,3,9,27。
18和27的公因数是 1,3,9。其中9最大,即18和27的最大的公因数是 9。
列举法
2.怎样求两个数的公因数和最大公因数?
18的因数:1,2,3,6,9,18。
筛选法
18和27的公因数是 1,3,9
18和27的最大公因数是 9。
如果要用边长是整分米数的正方形地砖把贮藏室的地面铺满(使用的地砖必须都是整块),可以选择边长是几分米的地砖?边长最大是几分米?
16dm
12dm
边长?dm
......
地砖的边长必须是12的因数。
......
......
......
......
......
......
......
地砖的边长应符合什么条件?
地砖的边长必须是16的因数。
......
16dm
12dm
......
画一画、
算一算
......
地砖的边长是16和12的公因数。
16的因数有 1, 2, 4, 8, 16。
12的因数有 1, 2, 3, 4,6,12。
16和12的公因数:
边长最大是 。
16的因数有 1, 2, 4, 8, 16。
答:可以选边长是1dm、2dm、4dm的地砖,边长最大是4dm。
16dm
12dm
边长=1dm
16dm
12dm
边长=2dm
16dm
12dm
边长=4dm
1.有一张长方形纸,长70cm,宽50cm。如果要剪成若干同样大小的正方形纸片而没有剩余,剪出的正方形纸片的边长最大是几厘米?
2.有两根小棒,长分别是14厘米,21厘米,要把它们截成同样长的小棒,没有剩余,每根小棒最长有多少厘米?
3.男、女生分别站成若干排,要使每排的人数相同,每排最多有多少人?这时男、女生分别有几排?
女生有36人。
男生有48人。
48÷12=4(排)
36÷12=3(排)
4.将一个长30厘米、宽24厘米、高18厘米的长方体木块锯成体积相等的小正方体木块,不能有剩余,那么小正方体的棱长最大是多少?能锯成多少块这样的小正方体?
5.给一面高27分米、长36分米的卧室墙面贴壁纸,要保证用整张的壁纸不能重叠且整好贴满,可以选择下列哪几种规格的壁纸?(单位:分米)
3
3
①
6
6
②
9
9
③
3
4
④
6
9
⑤
×
√
√
√
√
36÷4=9
27÷3=9
今天你有哪些收获?
