高中数学人教A版必修4课件-1.4.2正弦函数、余弦函数的性质(2) 14张PPT
文档属性
| 名称 | 高中数学人教A版必修4课件-1.4.2正弦函数、余弦函数的性质(2) 14张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1011.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览



文档简介
三角函数
1.4.2正弦函数余弦函数的性质
(二)
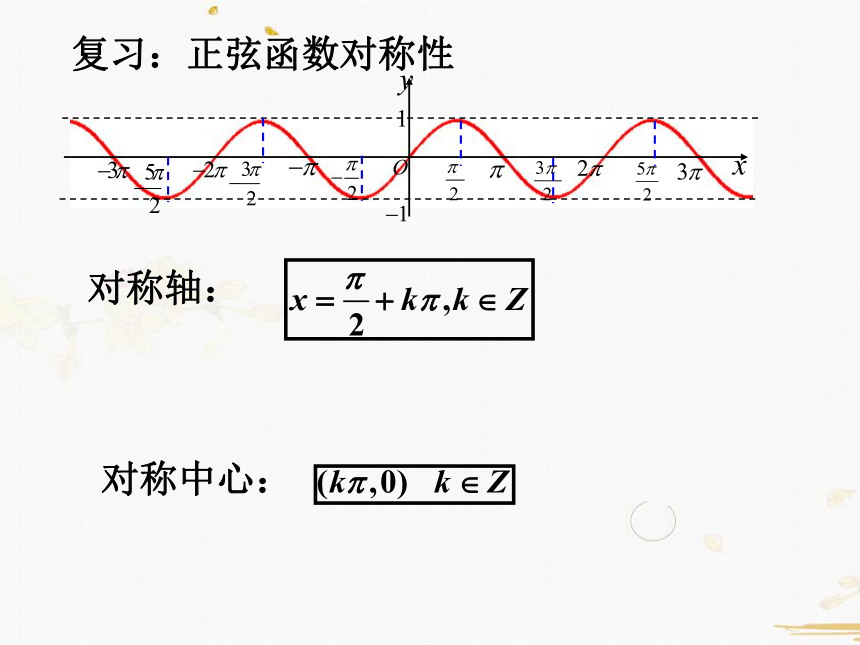
复习:正弦函数对称性
对称轴:
对称中心:
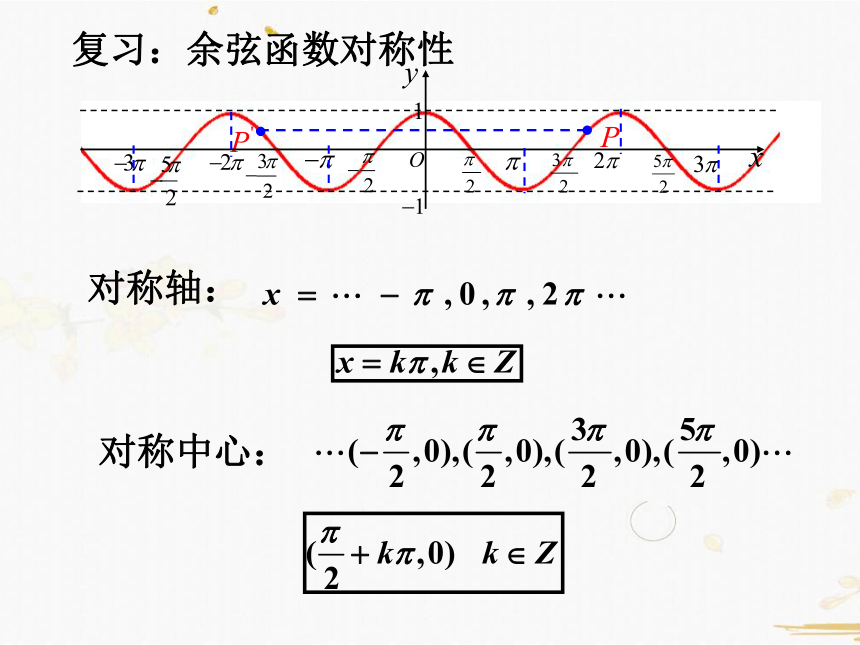
复习:余弦函数对称性
对称轴:
对称中心:
例 题
求 函数的对称轴和对称中心
解(1)令
则
的对称轴为
解得:对称轴为
的对称中心为
对称中心为
1、__________,则f(x)在这个区间上是增函数.
4.正弦余弦函数的单调性
函数
若在指定区间任取 ,
且 ,都有:
函数的单调性反映了函数在一个区间上的走向。
观察正余弦函数的图象,探究其单调性
2、__________,则f(x)在这个区间上是减函数.
增函数:上升
减函数:下降
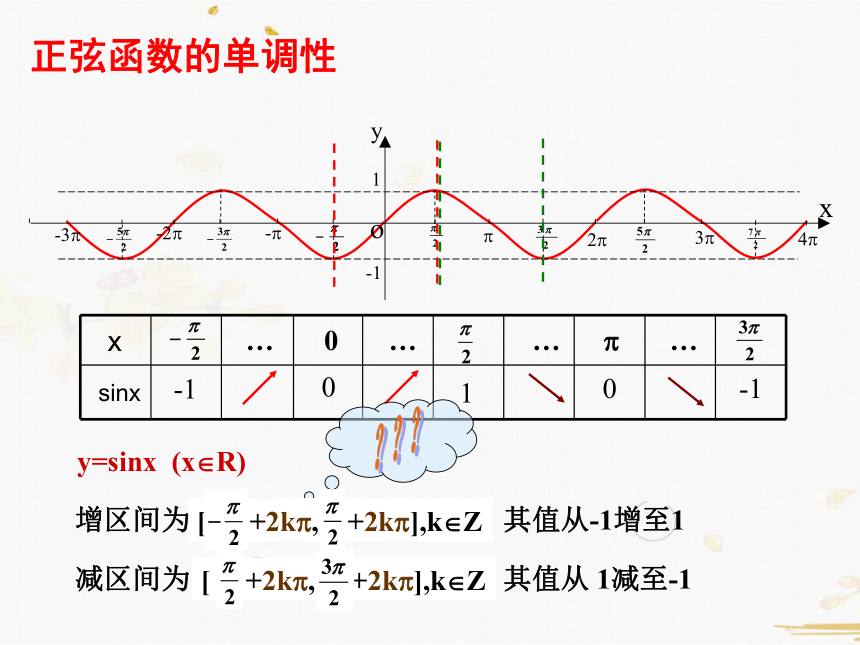
正弦函数的单调性
y=sinx (x?R)
增区间为 [ , ] 其值从-1增至1
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
x
sinx
… 0 … … ? …
-1
0
1
0
-1
减区间为 [ , ] 其值从 1减至-1
[ +2k?, +2k?],k?Z
[ +2k?, +2k?],k?Z
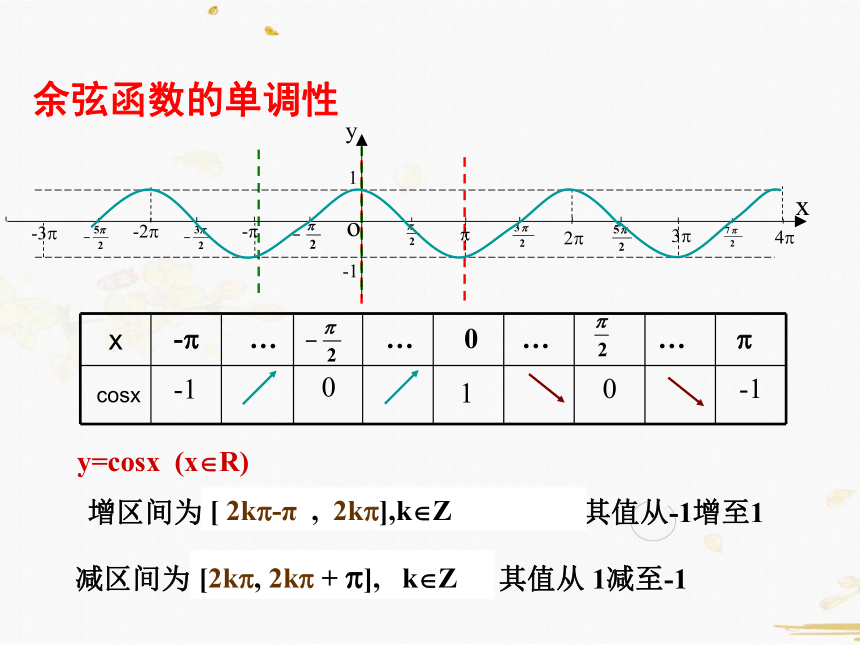
余弦函数的单调性
y=cosx (x?R)
x
cosx
-? … … 0 … … ?
-1
0
1
0
-1
减区间为 , 其值从 1减至-1
[2k?, 2k? + ?], k?Z
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
增区间为 其值从-1增至1
[ 2k?-π , 2k?],k?Z
练习
例3 比较下列各组数的大小:
学以致用
2.求函数的单调增区间
y=sinz的增区间
原函数的增区间
求函数的单调增区间
√
作业:
P46 习题A组 5
求 函数的对称轴和对称中心
1.4.2正弦函数余弦函数的性质
(二)
复习:正弦函数对称性
对称轴:
对称中心:
复习:余弦函数对称性
对称轴:
对称中心:
例 题
求 函数的对称轴和对称中心
解(1)令
则
的对称轴为
解得:对称轴为
的对称中心为
对称中心为
1、__________,则f(x)在这个区间上是增函数.
4.正弦余弦函数的单调性
函数
若在指定区间任取 ,
且 ,都有:
函数的单调性反映了函数在一个区间上的走向。
观察正余弦函数的图象,探究其单调性
2、__________,则f(x)在这个区间上是减函数.
增函数:上升
减函数:下降
正弦函数的单调性
y=sinx (x?R)
增区间为 [ , ] 其值从-1增至1
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
x
sinx
… 0 … … ? …
-1
0
1
0
-1
减区间为 [ , ] 其值从 1减至-1
[ +2k?, +2k?],k?Z
[ +2k?, +2k?],k?Z
余弦函数的单调性
y=cosx (x?R)
x
cosx
-? … … 0 … … ?
-1
0
1
0
-1
减区间为 , 其值从 1减至-1
[2k?, 2k? + ?], k?Z
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
增区间为 其值从-1增至1
[ 2k?-π , 2k?],k?Z
练习
例3 比较下列各组数的大小:
学以致用
2.求函数的单调增区间
y=sinz的增区间
原函数的增区间
求函数的单调增区间
√
作业:
P46 习题A组 5
求 函数的对称轴和对称中心
