高中数学人教A版必修4课件-1.4.2正弦函数、余弦函数的性质(3) 16张PPT
文档属性
| 名称 | 高中数学人教A版必修4课件-1.4.2正弦函数、余弦函数的性质(3) 16张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 935.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 17:46:27 | ||
图片预览



文档简介
三角函数
1.4.2正弦函数余弦函数的性质
(3)
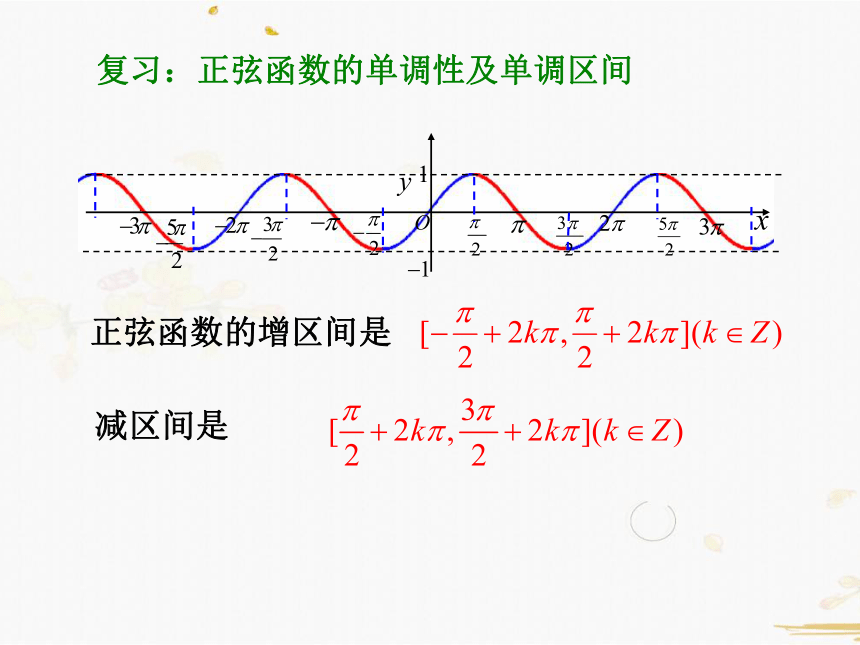
复习:正弦函数的单调性及单调区间
正弦函数的增区间是
减区间是
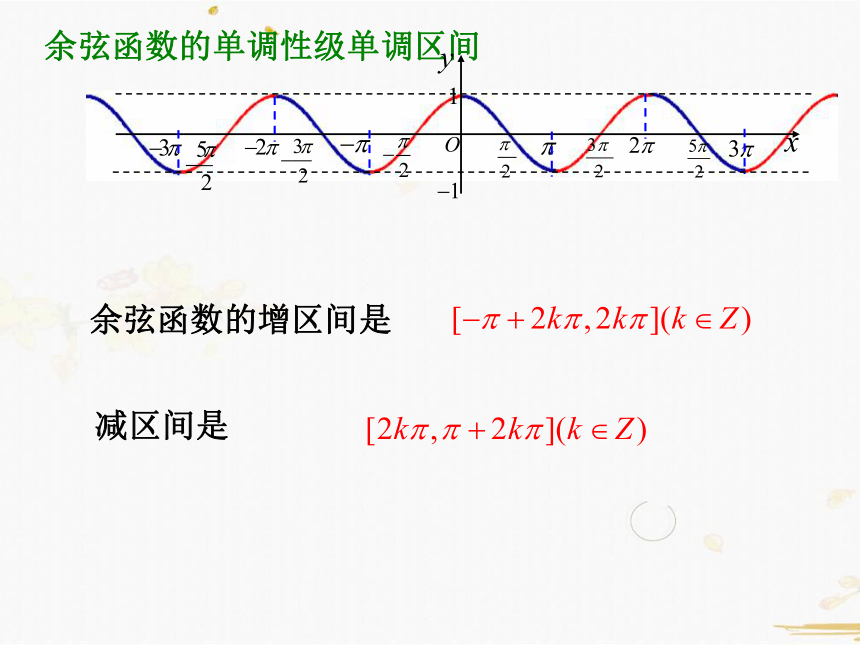
余弦函数的单调性级单调区间
余弦函数的增区间是
减区间是
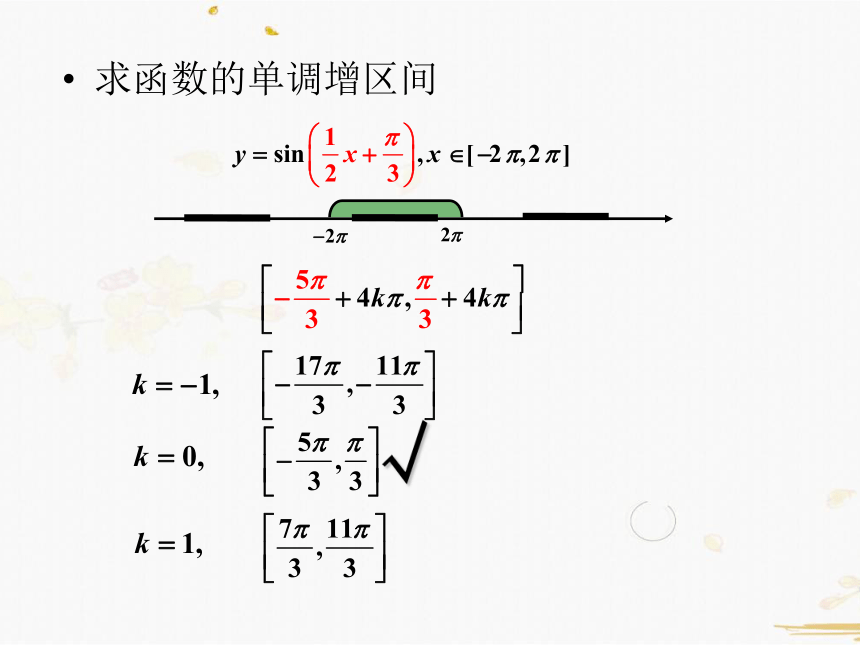
2.求函数的单调增区间
y=sinz的增区间
原函数的增区间
求函数的单调增区间
√
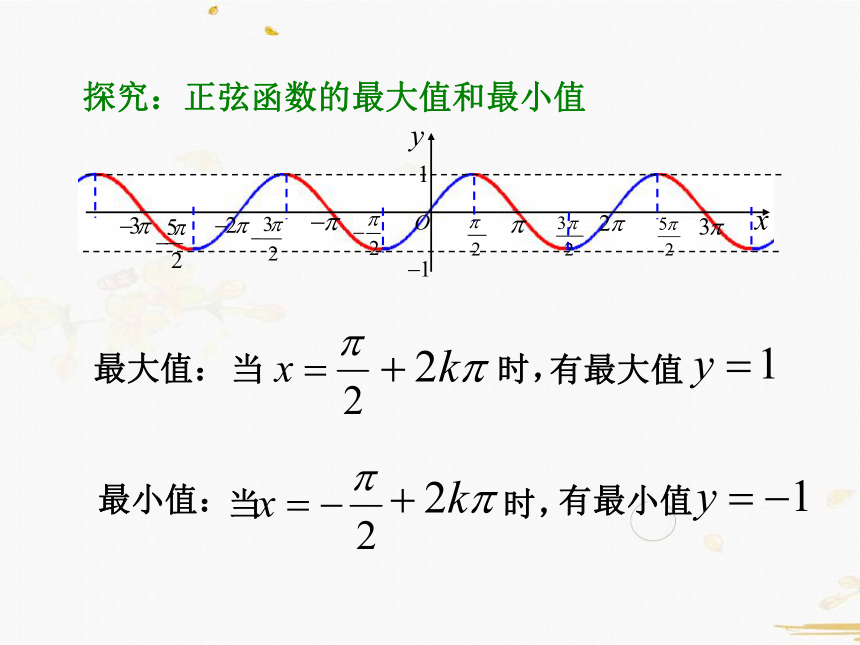
探究:正弦函数的最大值和最小值
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
探究:余弦函数的最大值和最小值
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
x
6?
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
当且仅当
当且仅当
当且仅当
当且仅当
五、正弦、余弦函数的最值
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
例2.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
这两个函数都有最大值、最小值.
(1)使函数 取得最大值的x的集合,就是使函数 取得最大值的x的集合
使函数 取得最小值的x的集合,就是
使函数 取得最小值的x的集合
函数 的最大值是1+1=2;最小值是
-1+1=0.
练习.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
(2)令t=2x,因为使函数 取最大值的t的集合是
所以使函数 取最大值的x的集合是
同理,使函数 取最小值的x的集合是
函数 取最大值是3,最小值是-3。
例题
求使函数 取得最大值、最小值的
自变量的集合,并写出最大值、最小值。
化未知为已知
分析:令
则
已知三角函数值求角
已知 求 的范围。
练习
小 结
1.求单调区间
(1)化未知为已知
(2)负号:sin提出来;cos消去
2.已知三角函数值,求角
(1)在一个区间里找两个代表
(2)分别加上2kπ
作业:
1、P46 习题A组 3题(2)、(3)
2、P41 第6题
1.4.2正弦函数余弦函数的性质
(3)
复习:正弦函数的单调性及单调区间
正弦函数的增区间是
减区间是
余弦函数的单调性级单调区间
余弦函数的增区间是
减区间是
2.求函数的单调增区间
y=sinz的增区间
原函数的增区间
求函数的单调增区间
√
探究:正弦函数的最大值和最小值
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
探究:余弦函数的最大值和最小值
最大值:
当 时,
有最大值
最小值:
当 时,
有最小值
x
6?
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
当且仅当
当且仅当
当且仅当
当且仅当
五、正弦、余弦函数的最值
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
例2.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
这两个函数都有最大值、最小值.
(1)使函数 取得最大值的x的集合,就是使函数 取得最大值的x的集合
使函数 取得最小值的x的集合,就是
使函数 取得最小值的x的集合
函数 的最大值是1+1=2;最小值是
-1+1=0.
练习.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
(2)令t=2x,因为使函数 取最大值的t的集合是
所以使函数 取最大值的x的集合是
同理,使函数 取最小值的x的集合是
函数 取最大值是3,最小值是-3。
例题
求使函数 取得最大值、最小值的
自变量的集合,并写出最大值、最小值。
化未知为已知
分析:令
则
已知三角函数值求角
已知 求 的范围。
练习
小 结
1.求单调区间
(1)化未知为已知
(2)负号:sin提出来;cos消去
2.已知三角函数值,求角
(1)在一个区间里找两个代表
(2)分别加上2kπ
作业:
1、P46 习题A组 3题(2)、(3)
2、P41 第6题
