高中数学人教A版必修4课件-2.2.3向量数乘运算及其几何意义 18张PPT
文档属性
| 名称 | 高中数学人教A版必修4课件-2.2.3向量数乘运算及其几何意义 18张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 858.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览





文档简介
§ 2.2.3向量数乘运算及其几何意义
A
E
D
C
B
1.向量加法三角形法则:
特点:首尾相接,顺次连
特点:共起点的对角线
B
A
O
特点:共起点,连终点,方向指被减数
2.向量加法平行四边形法则:
3.向量减法三角形法则:
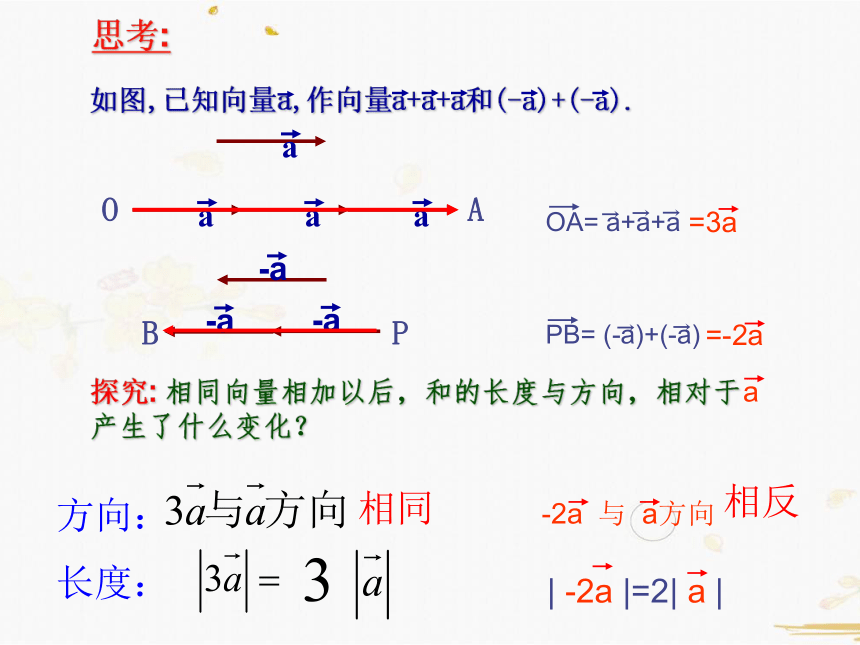
思考:
-a
如图,已知向量a,作向量a+a+a和(-a)+(-a).
a
a
-a
a
a
-a
OA= a+a+a
PB= (-a)+(-a)
=3a
=-2a
探究: 相同向量相加以后,和的长度与方向,相对于
产生了什么变化?
a
O
A
P
B
相同
相反
方向:
长度:
-2a
与 a方向
| -2a |=2| a |
定义:
特别地,当 λ=0 或 a = 0 时, λa = 0
(2) 方向 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
(1) 长度 |λa|=|λ|·|a|
一般地,实数λ与向量a的积是一个向量,这种运算叫做向量的数乘运算,记作λa。
它的长度和方向规定如下:
已知:向量
试从大小和方向两个角度,说说下面各向量与
的关系
说说看
2
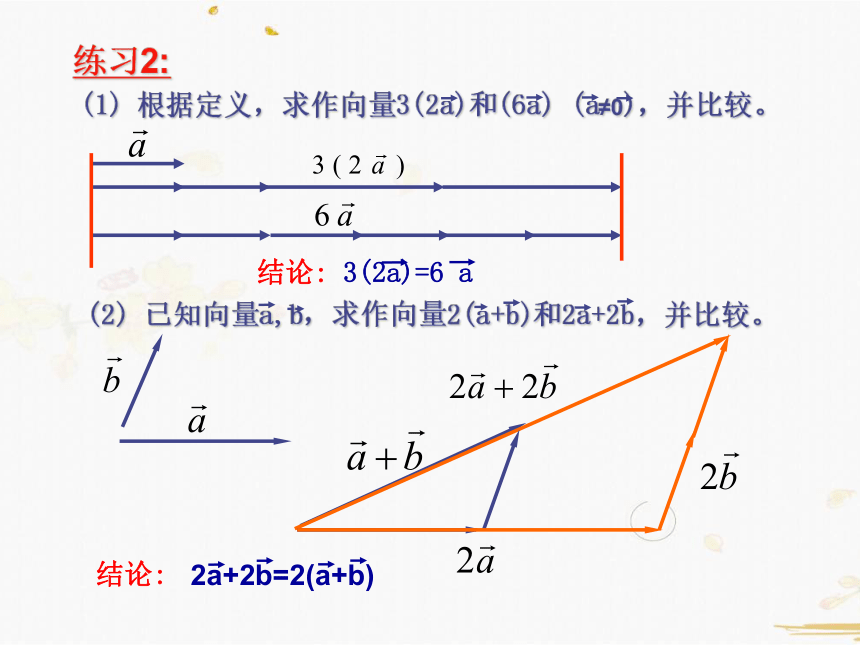
练习2:
结论:
2a+2b=2(a+b)
结论: 3(2a)=6 a
(1) 根据定义,求作向量3(2a)和(6a) (a≠0),并比较。
(2) 已知向量a,b,求作向量2(a+b)和2a+2b,并比较。
①λ(μa)=(λμ) a
运算律:
设a、b为任意向量,λ、μ为任意实数,则有:
②(λ+μ) a=λa+μa
③λ(a+b)=λa+λb
结合律
第一分配律
第二分配律
练习3:
解: (1) 原式 =
(2) 原式 =
(3) 原式 =
计算:(口答)
(1) (-3)×4 a
(2) 3( a+b) –2( a-b)-a
(3) (2a+3b-c) –(3a-2b+c )
(3-2-1)a+(3+2)b
= 5b
(2-3)a+(3+2)b+(-1-1)c
= -a+5b-2c
-12a
向量的加、减、数乘运算统称为向量的线性运算。
对于任意的向量 a,b 以及任意实数 λ,μ ,
恒有 λ(μ1a±μ2b)=
λμ1a±λμ2b
思考:
定理:
当a与b同方向时,有b=μa;
当a与b反方向时,有b=-μa,
所以始终有一个实数λ,使b=λa。
1、如果 b=λa , 那么,向量a与b是否共线?
2、如果非零向量a与b共线,那么是否有λ,使b=λa ?
对于向量a(a≠0)、b,如果有一个实数λ,使得b=λa , 那么,由数乘向量的定义知:向量a与b共线。
若向量a与b共线,a≠0,且向量b的长度是a的长度的μ(μ>0)倍,即有|b|=μ|a|,且
向量a(a≠0)与b共线, 当且仅当有唯一
一个实数λ,使b=λa.
思考:1) a为什么要是非零向量?
2) b 可以是零向量吗?
向量a(a≠0)与b共线, 当且仅当有唯一
一个实数λ,使b=λa.
点C在线段AB上,且AC︰CB = 2︰5
则
共线定理小练习
证明三点共线方法:
例1:
解:作图如右
O
A
B
C
依图猜想:A、B、C三点共线
∴ A、B、C三点共线.
a
b
b
b
已知任意两非零向量a、b,
试作 OA=a+b, OB=a+2b, OC=a+3b。
你能判断A、B、C三点之间的位置关系吗?为什么?
b
a
∵ AB=OB-OA
∴ AC=2AB
又 AC=OC-OA
=a+3b-(a+b)=2b
=a+2b-(a+b)=b
又 AB与AC有公共点A,
A
E
D
C
B
证明:
=3 AC
=3( AB+ BC )
∵ AB+BC=AC
=3 AB+3 BC
又 AE=AD+DE
∴ AC与AE 共线
如图,已知AD=3AB、DE=3BC,证明A、C、E三点共线。
又∵
AC与AE 有公共点A
∴ A、C、E三点共线
试一试
A
D
B
M
C
如图: ABCD的两条对角线交于点M,且 , 你能用 ,表示
吗?
例2:
表示 ,
= ,
在
ABCD中,设对角线
=
试用 ,
A
D
B
M
C
试一试
小结回顾:
二、知识应用:
1.证明 向量共线;
2.证明 三点共线: AB=λBC A,B,C三点共线;
3.证明 两直线平行:
AB=λCD AB∥CD
AB、CD不重合
直线AB∥直线CD
一、概念与定理
① λa 的定义及运算律
② 向量共线定理 ( a≠0 )
b=λa 向量a与b共线
教材P91ex.2.2剩余部分;
完成教辅相关部分;
3.预习教材P93~99.
课后作业
作业布置:
P91 第9、10、13题
A
E
D
C
B
1.向量加法三角形法则:
特点:首尾相接,顺次连
特点:共起点的对角线
B
A
O
特点:共起点,连终点,方向指被减数
2.向量加法平行四边形法则:
3.向量减法三角形法则:
思考:
-a
如图,已知向量a,作向量a+a+a和(-a)+(-a).
a
a
-a
a
a
-a
OA= a+a+a
PB= (-a)+(-a)
=3a
=-2a
探究: 相同向量相加以后,和的长度与方向,相对于
产生了什么变化?
a
O
A
P
B
相同
相反
方向:
长度:
-2a
与 a方向
| -2a |=2| a |
定义:
特别地,当 λ=0 或 a = 0 时, λa = 0
(2) 方向 当λ>0时,λa的方向与a方向相同;
当λ<0时,λa的方向与a方向相反;
(1) 长度 |λa|=|λ|·|a|
一般地,实数λ与向量a的积是一个向量,这种运算叫做向量的数乘运算,记作λa。
它的长度和方向规定如下:
已知:向量
试从大小和方向两个角度,说说下面各向量与
的关系
说说看
2
练习2:
结论:
2a+2b=2(a+b)
结论: 3(2a)=6 a
(1) 根据定义,求作向量3(2a)和(6a) (a≠0),并比较。
(2) 已知向量a,b,求作向量2(a+b)和2a+2b,并比较。
①λ(μa)=(λμ) a
运算律:
设a、b为任意向量,λ、μ为任意实数,则有:
②(λ+μ) a=λa+μa
③λ(a+b)=λa+λb
结合律
第一分配律
第二分配律
练习3:
解: (1) 原式 =
(2) 原式 =
(3) 原式 =
计算:(口答)
(1) (-3)×4 a
(2) 3( a+b) –2( a-b)-a
(3) (2a+3b-c) –(3a-2b+c )
(3-2-1)a+(3+2)b
= 5b
(2-3)a+(3+2)b+(-1-1)c
= -a+5b-2c
-12a
向量的加、减、数乘运算统称为向量的线性运算。
对于任意的向量 a,b 以及任意实数 λ,μ ,
恒有 λ(μ1a±μ2b)=
λμ1a±λμ2b
思考:
定理:
当a与b同方向时,有b=μa;
当a与b反方向时,有b=-μa,
所以始终有一个实数λ,使b=λa。
1、如果 b=λa , 那么,向量a与b是否共线?
2、如果非零向量a与b共线,那么是否有λ,使b=λa ?
对于向量a(a≠0)、b,如果有一个实数λ,使得b=λa , 那么,由数乘向量的定义知:向量a与b共线。
若向量a与b共线,a≠0,且向量b的长度是a的长度的μ(μ>0)倍,即有|b|=μ|a|,且
向量a(a≠0)与b共线, 当且仅当有唯一
一个实数λ,使b=λa.
思考:1) a为什么要是非零向量?
2) b 可以是零向量吗?
向量a(a≠0)与b共线, 当且仅当有唯一
一个实数λ,使b=λa.
点C在线段AB上,且AC︰CB = 2︰5
则
共线定理小练习
证明三点共线方法:
例1:
解:作图如右
O
A
B
C
依图猜想:A、B、C三点共线
∴ A、B、C三点共线.
a
b
b
b
已知任意两非零向量a、b,
试作 OA=a+b, OB=a+2b, OC=a+3b。
你能判断A、B、C三点之间的位置关系吗?为什么?
b
a
∵ AB=OB-OA
∴ AC=2AB
又 AC=OC-OA
=a+3b-(a+b)=2b
=a+2b-(a+b)=b
又 AB与AC有公共点A,
A
E
D
C
B
证明:
=3 AC
=3( AB+ BC )
∵ AB+BC=AC
=3 AB+3 BC
又 AE=AD+DE
∴ AC与AE 共线
如图,已知AD=3AB、DE=3BC,证明A、C、E三点共线。
又∵
AC与AE 有公共点A
∴ A、C、E三点共线
试一试
A
D
B
M
C
如图: ABCD的两条对角线交于点M,且 , 你能用 ,表示
吗?
例2:
表示 ,
= ,
在
ABCD中,设对角线
=
试用 ,
A
D
B
M
C
试一试
小结回顾:
二、知识应用:
1.证明 向量共线;
2.证明 三点共线: AB=λBC A,B,C三点共线;
3.证明 两直线平行:
AB=λCD AB∥CD
AB、CD不重合
直线AB∥直线CD
一、概念与定理
① λa 的定义及运算律
② 向量共线定理 ( a≠0 )
b=λa 向量a与b共线
教材P91ex.2.2剩余部分;
完成教辅相关部分;
3.预习教材P93~99.
课后作业
作业布置:
P91 第9、10、13题
