高中数学人教A版必修4课件-2.3.2-3 平面向量的坐标表示 19张PPT
文档属性
| 名称 | 高中数学人教A版必修4课件-2.3.2-3 平面向量的坐标表示 19张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 825.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 17:55:50 | ||
图片预览






文档简介
2.3 平面向量的坐标运算
2、什么是平面向量的基底?
1、平面向量基本定理
复习回顾:
那么当 与 垂直时,向量就可以分解为两个相互垂直的向量。这种分解称为向量的正交分解。
因此,可以建立直角坐标系进一步研究向量。
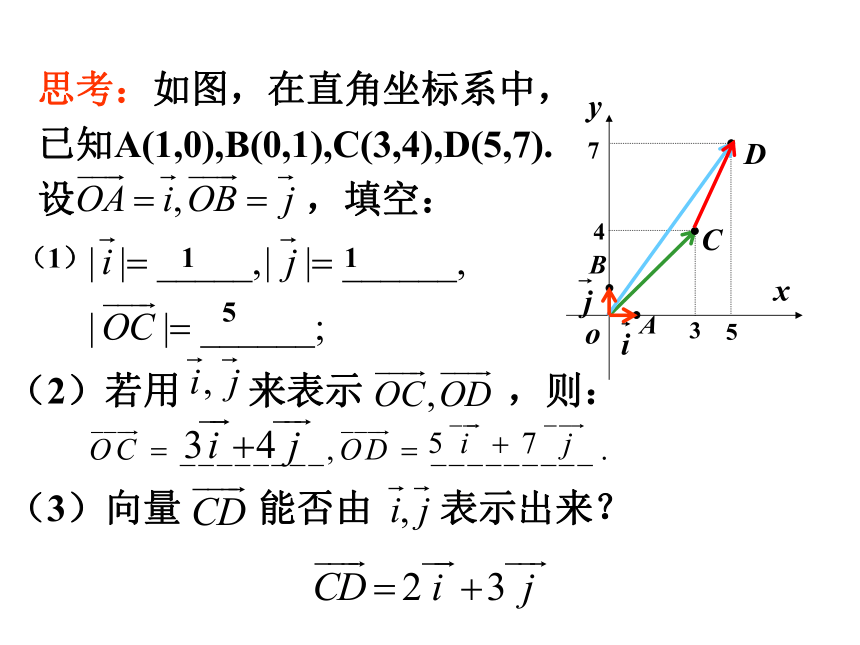
思考:如图,在直角坐标系中,
已知A(1,0),B(0,1),C(3,4),D(5,7).
设 ,填空:
(1)
(2)若用 来表示 ,则:
1
1
5
3
5
4
7
(3)向量 能否由 表示出来?
平面向量的坐标表示
如图, 是分别与x轴、y轴方向相同
的单位向量,若以 为基底,则
这里,我们把(x,y)叫做向量 的(直角)坐标,记作
①
其中,x叫做 在x轴上的坐标,y叫做 在
y轴上的坐标,①式叫做向量的坐标表示。
1 、把 a=x i+y j 称为向量基底形式.
2 、把(x , y)叫做向量a的(直角)坐标,
记为:a=(x , y) , 称其为向量的坐标形式.
3、 a=x i+y j =( x , y)
4、其中 x、 y 叫做 a 在x 、y轴上的坐标.
单位向量 i =(1,0),j =(0,1)
小结归纳:
5.两个向量相等的条件,利用坐标如何表示?
例1.如图,分别用基底 , 表示向量 、 、 、 ,并求出
它们的坐标。
A
A1
A2
解:如图可知
同理
思考:怎么求a+b,a-b呢?
1、平面向量的坐标运算
=(x1+x2,y1+y2)
一个向量的坐标等于此向量的有向线段的终点
O
X
Y
A(x1,y1)
B(x2,y2)
AB=OB-OA=(x2-x1,y2-y1)
已知 =(x1,y1), =(x2,y2),
同理 - =(x1-x2,y1-y2)
=(x1+x2) +(y1+y2)
则 + =(x1 +y1 )+(x2 +y2 )
已知 =(x,y)和实数λ,那么λ =(λx,λy)
2、向量的坐标:
坐标减去始点的坐标。
3、数乘向量的坐标:
例2.已知 ,求 的坐标。
课堂练习:
P100 第1(1)(2)、2、3(1)(2)
例5.如图,已知 的三个顶点A、B、C的坐标分别是
(-2,1)、(-1,3)、(3,4),试求顶点D的坐标。
A
B
C
D
x
y
O
解:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
课堂小结:
2 加、减法法则.
a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)
3 实数与向量积的运算法则:
λa =λ(x i+y j )=λx i+λy j
4 向量坐标.
若A(x1 , y1) , B(x2 , y2)
1 向量坐标定义.
则 =(x2 - x1 , y2 – y1 )
a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)
作业布置:
P101 A组 第1、3题
练习巩固
坐标是
A、(3,2) B、(2,3) C、(-3,-2) D、(-2,-3)
B
A、x=1,y=3 B、x=3,y=1
C、x=1,y=-3 D、x=5,y=-1
B
标
坐标为
A、(x-2,y+1) B、(x+2,y-1)
C、(-2-x,1-y) D、(x+2,y+1)
C
B
B
标
的坐标为(i,j),则点A
的坐标为
A、(m-i,n-j) B、(i-m,j-n)
C、(m+i,n+j) D、(m+n,i+j)
A
A
8、平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C(x,y)满足
其中α,β∈R,且α+β=1,则x,y所满足的关系式为
A、3x+2y-11=0 B、(x-1)2+(y-2)2=5
C、2x-y=0 D、x+2y-5=0
D
9、若M、N两点的坐标分别为(2,4)和(-2,1),则
的坐标为__________,
的坐标为_________
(-4,-3)
(4, 3)
则点B的坐标是__________
(5,4)
12、作用于原点的两个力
为使它们
平衡,需加力
(-6,2)
(-3,-4)
坐标
解:设C(x1,y1),D(x2,y2),
(例1变式)
2、什么是平面向量的基底?
1、平面向量基本定理
复习回顾:
那么当 与 垂直时,向量就可以分解为两个相互垂直的向量。这种分解称为向量的正交分解。
因此,可以建立直角坐标系进一步研究向量。
思考:如图,在直角坐标系中,
已知A(1,0),B(0,1),C(3,4),D(5,7).
设 ,填空:
(1)
(2)若用 来表示 ,则:
1
1
5
3
5
4
7
(3)向量 能否由 表示出来?
平面向量的坐标表示
如图, 是分别与x轴、y轴方向相同
的单位向量,若以 为基底,则
这里,我们把(x,y)叫做向量 的(直角)坐标,记作
①
其中,x叫做 在x轴上的坐标,y叫做 在
y轴上的坐标,①式叫做向量的坐标表示。
1 、把 a=x i+y j 称为向量基底形式.
2 、把(x , y)叫做向量a的(直角)坐标,
记为:a=(x , y) , 称其为向量的坐标形式.
3、 a=x i+y j =( x , y)
4、其中 x、 y 叫做 a 在x 、y轴上的坐标.
单位向量 i =(1,0),j =(0,1)
小结归纳:
5.两个向量相等的条件,利用坐标如何表示?
例1.如图,分别用基底 , 表示向量 、 、 、 ,并求出
它们的坐标。
A
A1
A2
解:如图可知
同理
思考:怎么求a+b,a-b呢?
1、平面向量的坐标运算
=(x1+x2,y1+y2)
一个向量的坐标等于此向量的有向线段的终点
O
X
Y
A(x1,y1)
B(x2,y2)
AB=OB-OA=(x2-x1,y2-y1)
已知 =(x1,y1), =(x2,y2),
同理 - =(x1-x2,y1-y2)
=(x1+x2) +(y1+y2)
则 + =(x1 +y1 )+(x2 +y2 )
已知 =(x,y)和实数λ,那么λ =(λx,λy)
2、向量的坐标:
坐标减去始点的坐标。
3、数乘向量的坐标:
例2.已知 ,求 的坐标。
课堂练习:
P100 第1(1)(2)、2、3(1)(2)
例5.如图,已知 的三个顶点A、B、C的坐标分别是
(-2,1)、(-1,3)、(3,4),试求顶点D的坐标。
A
B
C
D
x
y
O
解:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
课堂小结:
2 加、减法法则.
a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)
3 实数与向量积的运算法则:
λa =λ(x i+y j )=λx i+λy j
4 向量坐标.
若A(x1 , y1) , B(x2 , y2)
1 向量坐标定义.
则 =(x2 - x1 , y2 – y1 )
a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)
作业布置:
P101 A组 第1、3题
练习巩固
坐标是
A、(3,2) B、(2,3) C、(-3,-2) D、(-2,-3)
B
A、x=1,y=3 B、x=3,y=1
C、x=1,y=-3 D、x=5,y=-1
B
标
坐标为
A、(x-2,y+1) B、(x+2,y-1)
C、(-2-x,1-y) D、(x+2,y+1)
C
B
B
标
的坐标为(i,j),则点A
的坐标为
A、(m-i,n-j) B、(i-m,j-n)
C、(m+i,n+j) D、(m+n,i+j)
A
A
8、平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C(x,y)满足
其中α,β∈R,且α+β=1,则x,y所满足的关系式为
A、3x+2y-11=0 B、(x-1)2+(y-2)2=5
C、2x-y=0 D、x+2y-5=0
D
9、若M、N两点的坐标分别为(2,4)和(-2,1),则
的坐标为__________,
的坐标为_________
(-4,-3)
(4, 3)
则点B的坐标是__________
(5,4)
12、作用于原点的两个力
为使它们
平衡,需加力
(-6,2)
(-3,-4)
坐标
解:设C(x1,y1),D(x2,y2),
(例1变式)
