高中数学人教A版必修4课件-3.1.1两角差的余弦公式 15张PPT
文档属性
| 名称 | 高中数学人教A版必修4课件-3.1.1两角差的余弦公式 15张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 543.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-04 00:00:00 | ||
图片预览



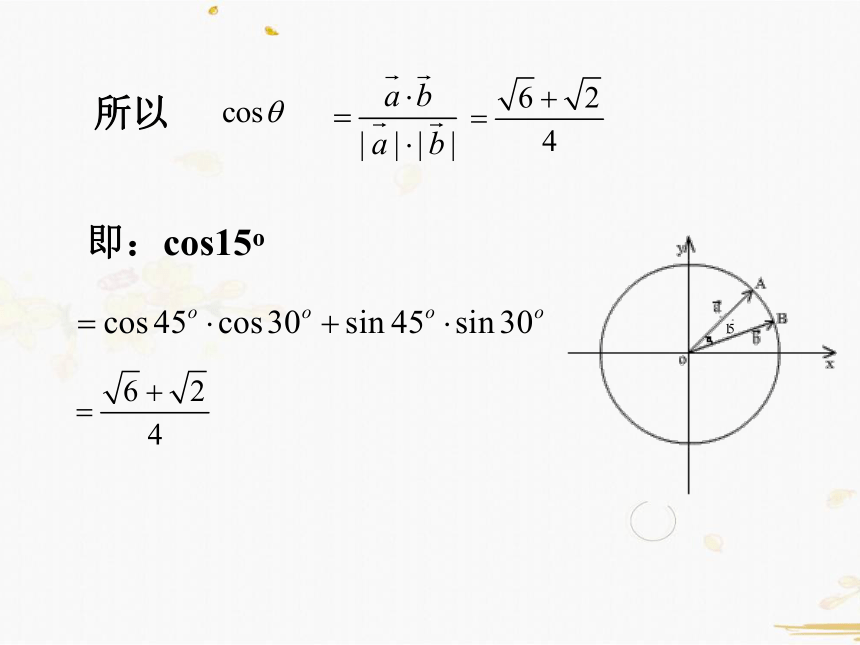
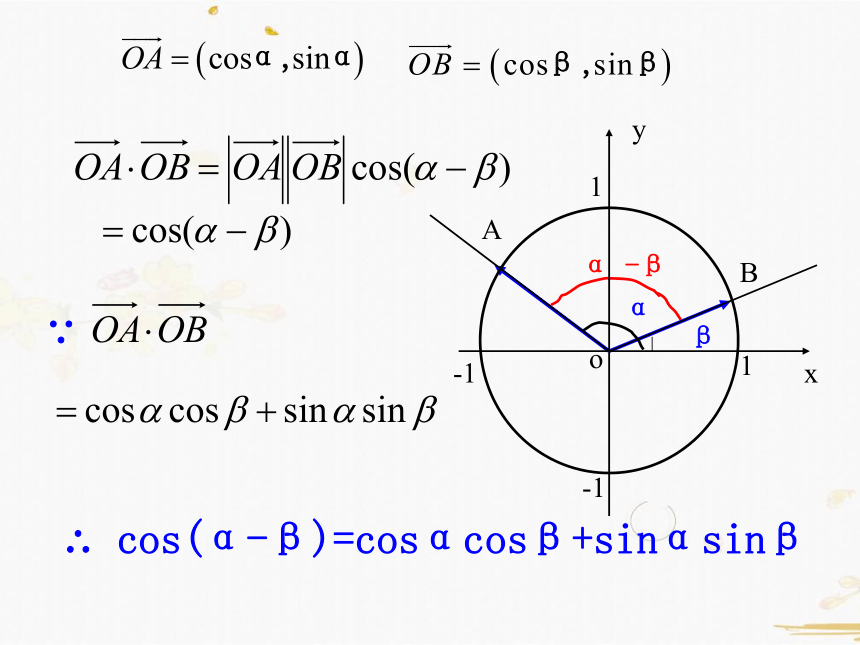


文档简介
3.1.1 两角差的余弦公式
其中θ∈[0,π ]
两个向量的数量积
温
故
知
新
!
复习回顾: 向量的数量积以及两个向量夹角的余弦值公式.
练习:已知向量 , ,求 夹角 的余弦
解:
所以
即:cos15o
-1
1
1
-1
α -β
B
A
y
x
o
β
α
∵
∴ cos(α-β)=cosαcosβ+sinαsinβ
差角的余弦公式
结
论
归
纳
对于任意角
注意:1.公式的结构特点;
2.对于α,β,只要知道其正弦或余弦,就可以求出cos(α-β)
不查表,求cos15°的值.
解: cos15 ° =cos(45 °– 30 °)
=cos45 °cos30 ° +sin45 °sin30 °
应用举例
思考:你会求 的值吗?
学
以
致
用
!
例1已知
求 的值.
解:
∵
∴
例2.已知
求cos(α-β)的值
练习:
思考题:已知 都是锐角,
变角:
分析:
三角函数中一定要注意观察角度之间的关系,例如
课堂练习:
P127 练习 3、4题
课堂小结:
1、两角差的余弦公式
对于任意角α,β都有
cos(α-β)=cosαcosβ+sinαsinβ
2、公式的结构特点及应用
作业布置
P137 A组 第2,3,4题
其中θ∈[0,π ]
两个向量的数量积
温
故
知
新
!
复习回顾: 向量的数量积以及两个向量夹角的余弦值公式.
练习:已知向量 , ,求 夹角 的余弦
解:
所以
即:cos15o
-1
1
1
-1
α -β
B
A
y
x
o
β
α
∵
∴ cos(α-β)=cosαcosβ+sinαsinβ
差角的余弦公式
结
论
归
纳
对于任意角
注意:1.公式的结构特点;
2.对于α,β,只要知道其正弦或余弦,就可以求出cos(α-β)
不查表,求cos15°的值.
解: cos15 ° =cos(45 °– 30 °)
=cos45 °cos30 ° +sin45 °sin30 °
应用举例
思考:你会求 的值吗?
学
以
致
用
!
例1已知
求 的值.
解:
∵
∴
例2.已知
求cos(α-β)的值
练习:
思考题:已知 都是锐角,
变角:
分析:
三角函数中一定要注意观察角度之间的关系,例如
课堂练习:
P127 练习 3、4题
课堂小结:
1、两角差的余弦公式
对于任意角α,β都有
cos(α-β)=cosαcosβ+sinαsinβ
2、公式的结构特点及应用
作业布置
P137 A组 第2,3,4题
