五年级下册数学课件 稍复杂的找次品问题 人教版(共30张PPT)
文档属性
| 名称 | 五年级下册数学课件 稍复杂的找次品问题 人教版(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
第八单元 数学广角—找次品
第2课时 稍复杂的找次品问题
五年级数学下册(RJ)教学课件
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
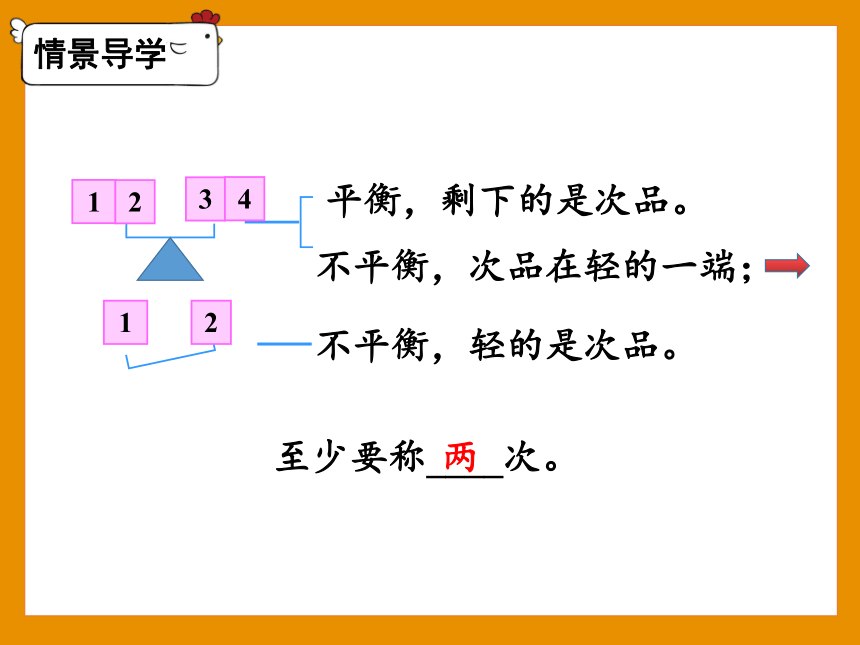
有5盒饼干,其中的4盒质量相同,另有1盒少了几块。如果能用天平称,至少称几次可以保证找出这盒饼干,请用图文表示出过程。
情景导学
平衡,剩下的是次品。
不平衡,次品在轻的一端;
1
2
3
4
1
2
不平衡,轻的是次品。
至少要称____次。
两
第二部分
学习目标
学习目标
通过观察、猜测、试验、推理等活动,体会解决问题策略的多样性及运用优化的方法解决问题的有效性。
第三部分
探究与发现
探索与发现
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
是指肯定能找出次品的最少次数。
“至少称几次就保证……”是什么意思?
探索与发现
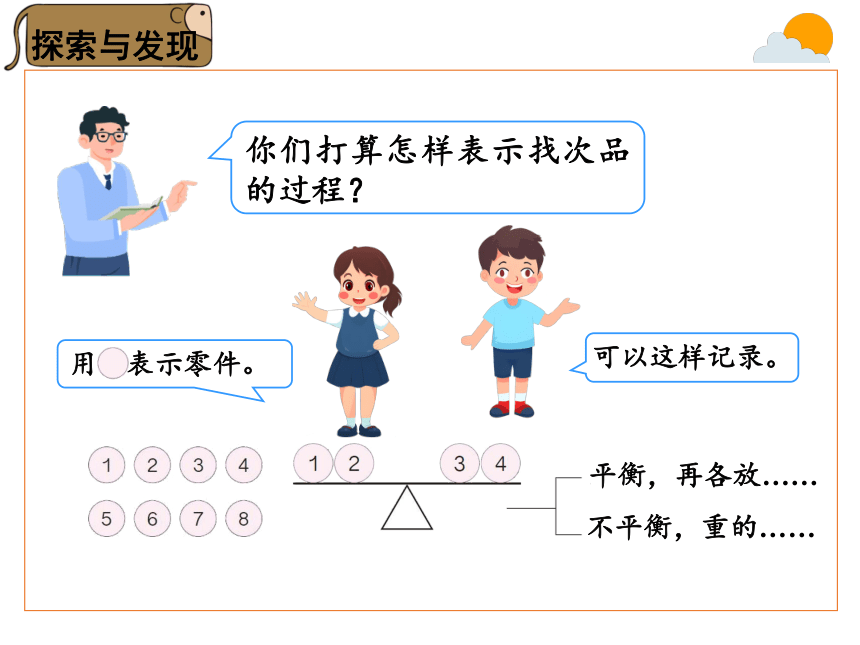
你们打算怎样表示找次品的过程?
用 表示零件。
可以这样记录。
平衡,再各放……
不平衡,重的……
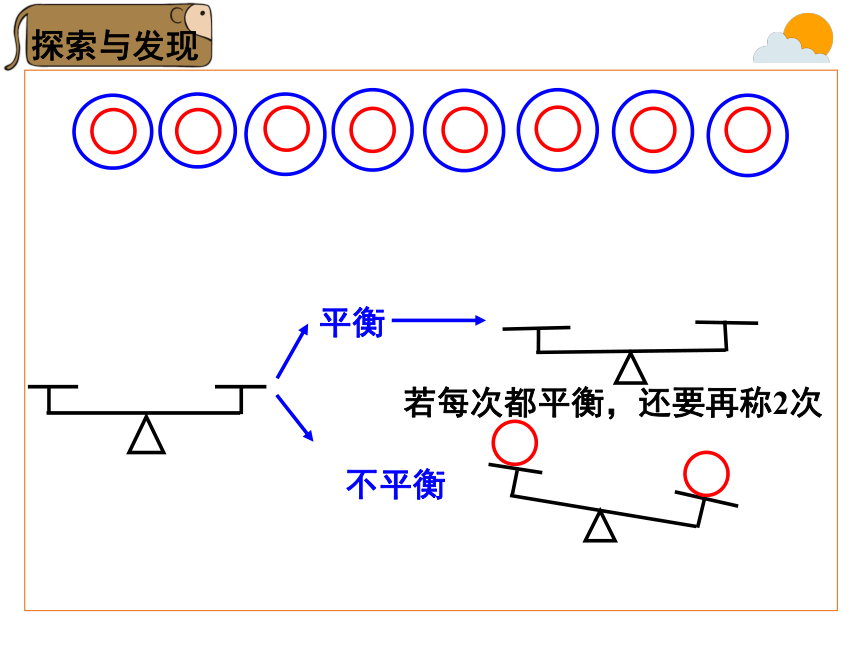
探索与发现
平衡
不平衡
若每次都平衡,还要再称2次
探索与发现
平衡
不平衡
还要再称1次
再称1次
探索与发现
平衡
不平衡
再称1次
在余下的2瓶中,
还要再称1次。
用图形表示:
探索与发现
不平衡
还要再称1次
探索与发现
每次每边放的个数 分成的份数 至少要称的次数
将探索的情况填入下表。
4
2
4
8
1
4
2
3
3
3
3
2
(1)表中哪种方法需要称的次数最少
探索与发现
(1)“分成的份数”、分的方法与找出次品所要称的次数有什么关系
(2)怎样分找出次品需要称的次数最少
9个零件里有1个是次品(次品重一些),假如用天平称,至少称几次就保证一定能找出次品
观察完成的表格,你发现了什么
探索与发现
平衡
不平衡
7个零件至少称2次
探索与发现
平衡
不平衡
再称1次
在余下的3个里
再称1次
探索与发现
平衡
不平衡
再称2次
在余下的5个里
再称1次
探索与发现
用你发现的方法找出10个、11个零件中的1个次品(次品重一些),看看是不是保证找出次品的次数也是最少的。
不能平均分的,也应使多的与少的一份只差1。这样不但能保证找出次品,而且称的次数一定最少。
利用天平找次品的时候,把待分的物品分成3份,能够平均分的平均分成3份。
第四部分
学以致用
学以致用
(课本P113练习二十七)
(1)如果用天平称,你打算怎样称?你能表示出称的过程吗?
我吃了 2 个。
这 9 筐里你吃
的是哪一筐
300 g/筐
学以致用
(课本P113练习二十七)
1
2
平衡。
不平衡,轻的是次品。
不平衡,轻的是次品。
平衡。
1
3
2
4
不平衡,轻的是次品。
平衡。
1
3
2
4
5
6
1
3
2
4
5
6
7
8
不平衡,轻的是次品。
平衡,次品是第9筐。
学以致用
(课本P113练习二十七)
(2)用你的方法称几次可以保证找出来
称4次可以保证找出来。
(3)你能称 2 次就保证把它找出来吗
将 9 筐分成 3 份(3,3,3),①天平两边分别放 3 筐,若天平平衡,则轻的一筐在剩余的三筐中。② 再从剩余三筐中取两筐,分别放在天平两盘中各一筐,若分出轻重,则放在轻的一边的一筐即为小松树吃的那一筐;若天平仍平衡,则剩余的一筐即为小松鼠吃的那一筐。若第①步天平不平衡,则从较轻的三筐中取两筐,操作如②。
(4)如果天平两边各放 4 筐,称一次有可能称出来吗
有可能。
学以致用
(课本P114练习二十七)
有3袋白糖,其中2袋每袋500g,另一袋不是500g,但不知道比500g重还是轻。你能用天平找出来吗
1
2
平衡,剩下的第3袋不是500g。
不平衡。
1
3
平衡,第2袋不是500g。
不平衡,第1袋不是500g。
学以致用
(课本P114练习二十七)
把白糖分成3份,第一次天平两边各放一袋白糖,若天平平衡,则剩下的那袋是次品,再称一次就能判断出次品还是重了;若天平不平衡,这两袋中一定有一袋是次品,可取出轻(重)的那袋,把剩下的那袋放上天平,若天平平衡,则轻(重)的是次品,若天平不平衡,则重(轻)的是次品。
学以致用
你知道吗?用天平找次品时,所测物品数目与测试的次数有以下关系(只含一个次品,已知次品比正品重或轻。)
要辨别的物品数目 保证能找出次品需要的次数
2~3 4~9 10~27 28~81 82~243 …… 1
2
3
4
5
……
(1)要保证6次能测出次品,待测物品可能是多少个
(2)从左表中你能发现什么规律 为什么
第五部分
课堂小结
知识小结
1.通过观察、猜测、试验、推理等活动,体会解决问题策略的多样性及运用优化的方法解决问题的有效性,感受优化思想。
2.尝试用数学的方法来解决实际生活中的简单问题。
3.培养数学的应用意识和解决问题的能力,同时培养探索和创新精神。
稍复杂的找次品问题
谢谢观看
下课!
第八单元 数学广角—找次品
第2课时 稍复杂的找次品问题
五年级数学下册(RJ)教学课件
目录
CONTENTS
情景导入
01
学习目标
02
探究与发现
03
学以致用
04
课后作业
06
课堂小结
05
情景导学
第一部分
情景导学
有5盒饼干,其中的4盒质量相同,另有1盒少了几块。如果能用天平称,至少称几次可以保证找出这盒饼干,请用图文表示出过程。
情景导学
平衡,剩下的是次品。
不平衡,次品在轻的一端;
1
2
3
4
1
2
不平衡,轻的是次品。
至少要称____次。
两
第二部分
学习目标
学习目标
通过观察、猜测、试验、推理等活动,体会解决问题策略的多样性及运用优化的方法解决问题的有效性。
第三部分
探究与发现
探索与发现
8个零件里有1个是次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
是指肯定能找出次品的最少次数。
“至少称几次就保证……”是什么意思?
探索与发现
你们打算怎样表示找次品的过程?
用 表示零件。
可以这样记录。
平衡,再各放……
不平衡,重的……
探索与发现
平衡
不平衡
若每次都平衡,还要再称2次
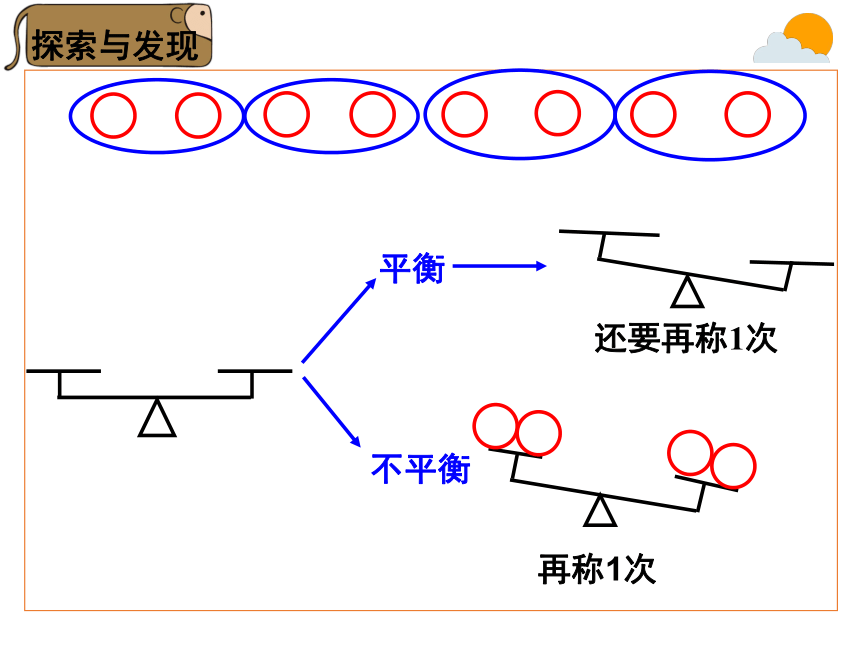
探索与发现
平衡
不平衡
还要再称1次
再称1次
探索与发现
平衡
不平衡
再称1次
在余下的2瓶中,
还要再称1次。
用图形表示:
探索与发现
不平衡
还要再称1次
探索与发现
每次每边放的个数 分成的份数 至少要称的次数
将探索的情况填入下表。
4
2
4
8
1
4
2
3
3
3
3
2
(1)表中哪种方法需要称的次数最少
探索与发现
(1)“分成的份数”、分的方法与找出次品所要称的次数有什么关系
(2)怎样分找出次品需要称的次数最少
9个零件里有1个是次品(次品重一些),假如用天平称,至少称几次就保证一定能找出次品
观察完成的表格,你发现了什么
探索与发现
平衡
不平衡
7个零件至少称2次
探索与发现
平衡
不平衡
再称1次
在余下的3个里
再称1次
探索与发现
平衡
不平衡
再称2次
在余下的5个里
再称1次
探索与发现
用你发现的方法找出10个、11个零件中的1个次品(次品重一些),看看是不是保证找出次品的次数也是最少的。
不能平均分的,也应使多的与少的一份只差1。这样不但能保证找出次品,而且称的次数一定最少。
利用天平找次品的时候,把待分的物品分成3份,能够平均分的平均分成3份。
第四部分
学以致用
学以致用
(课本P113练习二十七)
(1)如果用天平称,你打算怎样称?你能表示出称的过程吗?
我吃了 2 个。
这 9 筐里你吃
的是哪一筐
300 g/筐
学以致用
(课本P113练习二十七)
1
2
平衡。
不平衡,轻的是次品。
不平衡,轻的是次品。
平衡。
1
3
2
4
不平衡,轻的是次品。
平衡。
1
3
2
4
5
6
1
3
2
4
5
6
7
8
不平衡,轻的是次品。
平衡,次品是第9筐。
学以致用
(课本P113练习二十七)
(2)用你的方法称几次可以保证找出来
称4次可以保证找出来。
(3)你能称 2 次就保证把它找出来吗
将 9 筐分成 3 份(3,3,3),①天平两边分别放 3 筐,若天平平衡,则轻的一筐在剩余的三筐中。② 再从剩余三筐中取两筐,分别放在天平两盘中各一筐,若分出轻重,则放在轻的一边的一筐即为小松树吃的那一筐;若天平仍平衡,则剩余的一筐即为小松鼠吃的那一筐。若第①步天平不平衡,则从较轻的三筐中取两筐,操作如②。
(4)如果天平两边各放 4 筐,称一次有可能称出来吗
有可能。
学以致用
(课本P114练习二十七)
有3袋白糖,其中2袋每袋500g,另一袋不是500g,但不知道比500g重还是轻。你能用天平找出来吗
1
2
平衡,剩下的第3袋不是500g。
不平衡。
1
3
平衡,第2袋不是500g。
不平衡,第1袋不是500g。
学以致用
(课本P114练习二十七)
把白糖分成3份,第一次天平两边各放一袋白糖,若天平平衡,则剩下的那袋是次品,再称一次就能判断出次品还是重了;若天平不平衡,这两袋中一定有一袋是次品,可取出轻(重)的那袋,把剩下的那袋放上天平,若天平平衡,则轻(重)的是次品,若天平不平衡,则重(轻)的是次品。
学以致用
你知道吗?用天平找次品时,所测物品数目与测试的次数有以下关系(只含一个次品,已知次品比正品重或轻。)
要辨别的物品数目 保证能找出次品需要的次数
2~3 4~9 10~27 28~81 82~243 …… 1
2
3
4
5
……
(1)要保证6次能测出次品,待测物品可能是多少个
(2)从左表中你能发现什么规律 为什么
第五部分
课堂小结
知识小结
1.通过观察、猜测、试验、推理等活动,体会解决问题策略的多样性及运用优化的方法解决问题的有效性,感受优化思想。
2.尝试用数学的方法来解决实际生活中的简单问题。
3.培养数学的应用意识和解决问题的能力,同时培养探索和创新精神。
稍复杂的找次品问题
谢谢观看
下课!
