2020-2021学年人教版九年级数学下册课件-27.2.1 相似三角形的判定(17张)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册课件-27.2.1 相似三角形的判定(17张) |  | |
| 格式 | pptx | ||
| 文件大小 | 322.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 09:08:14 | ||
图片预览

文档简介
相似三角形的判定
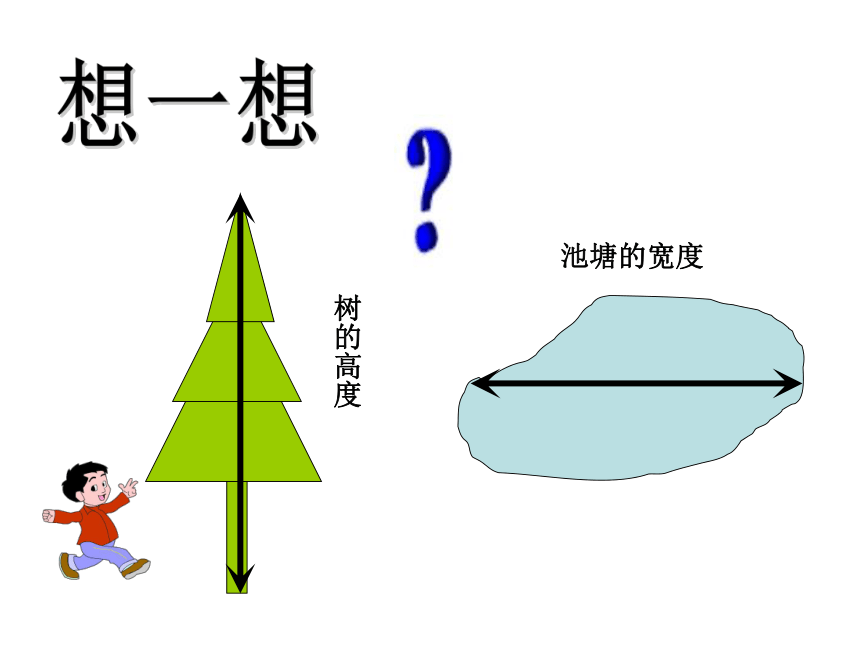
想一想
树的高度
池塘的宽度
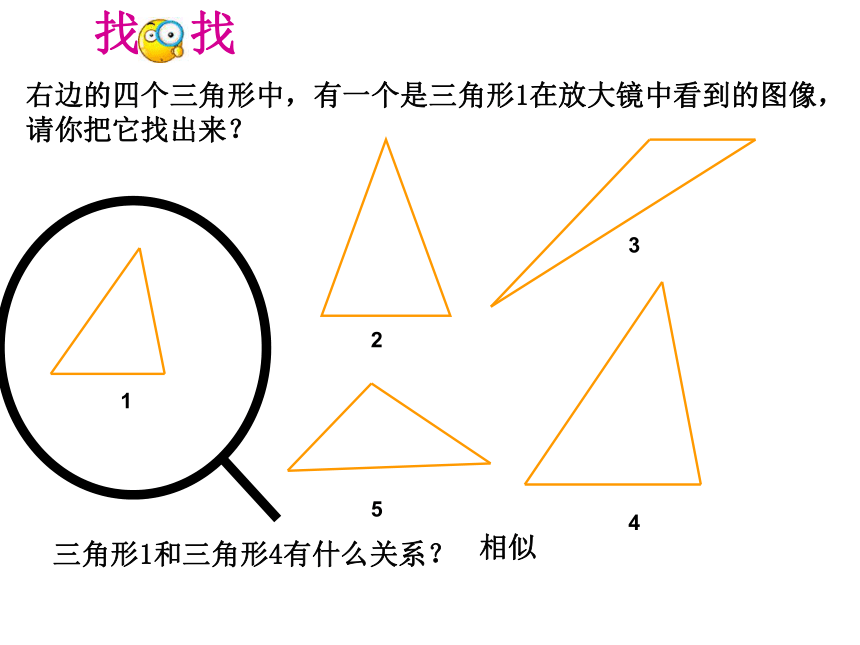
右边的四个三角形中,有一个是三角形1在放大镜中看到的图像,
请你把它找出来?
三角形1和三角形4有什么关系?
相似
1
找一找
5
2
3
4
A
B
C
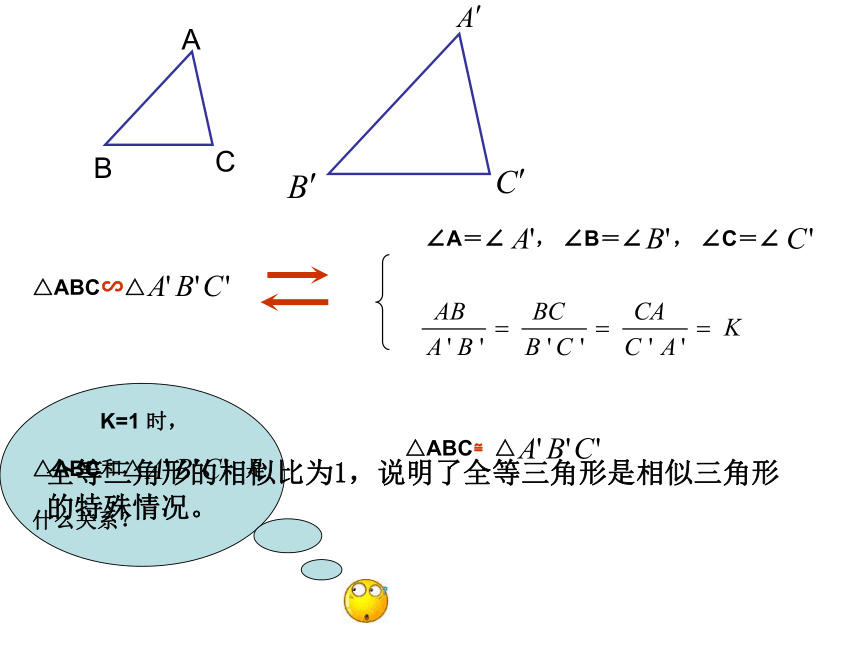
△ABC∽△
K=1 时,
△ABC和△ 是
什么关系?
△ABC≌△
全等三角形的相似比为1,说明了全等三角形是相似三角形的特殊情况。
∠A=∠ , ∠B=∠ , ∠C=∠
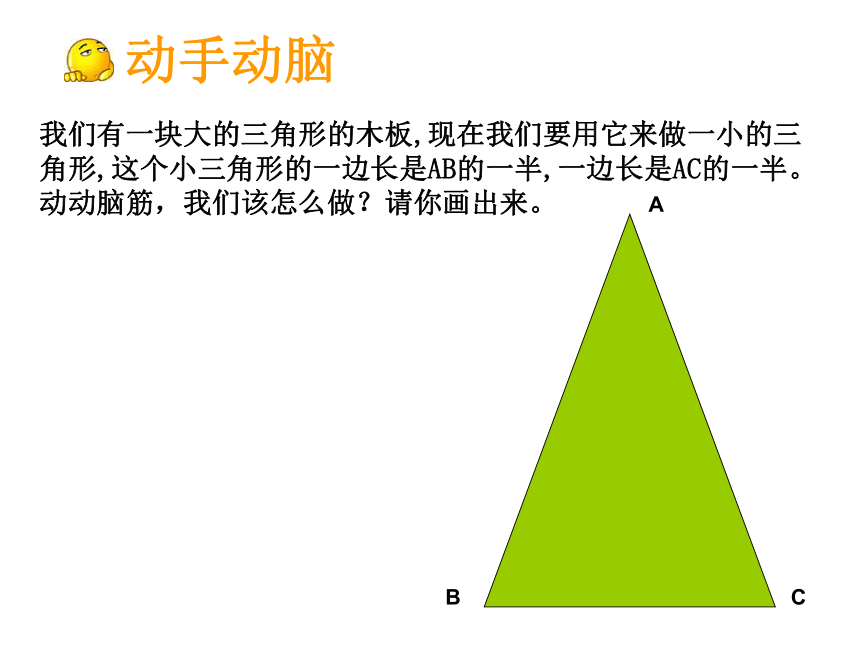
我们有一块大的三角形的木板,现在我们要用它来做一小的三角形,这个小三角形的一边长是AB的一半,一边长是AC的一半。动动脑筋,我们该怎么做?请你画出来。
动手动脑
A
B
C
D
E
A
B
C
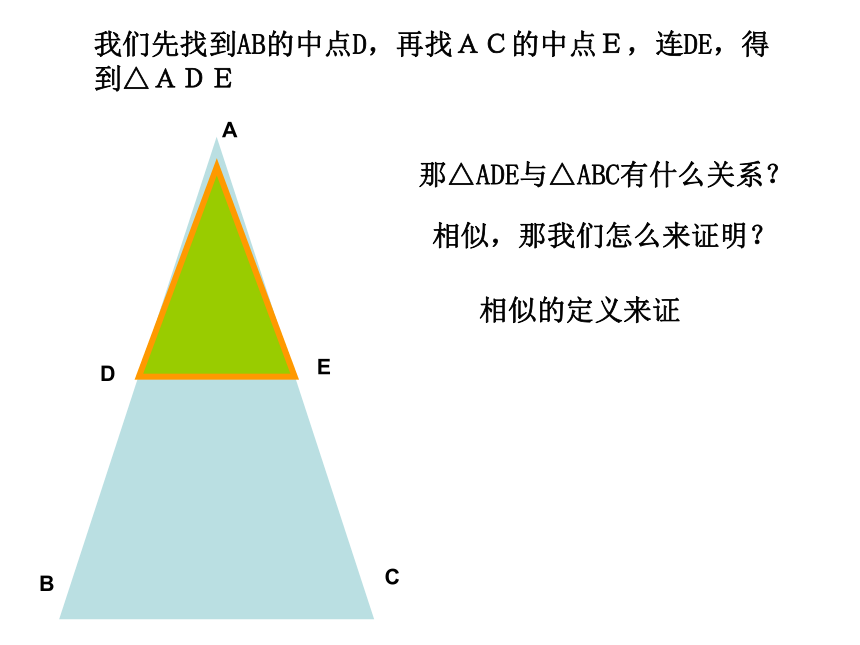
我们先找到AB的中点D,再找AC的中点E,连DE,得
到△ADE
那△ADE与△ABC有什么关系?
相似,那我们怎么来证明?
相似的定义来证
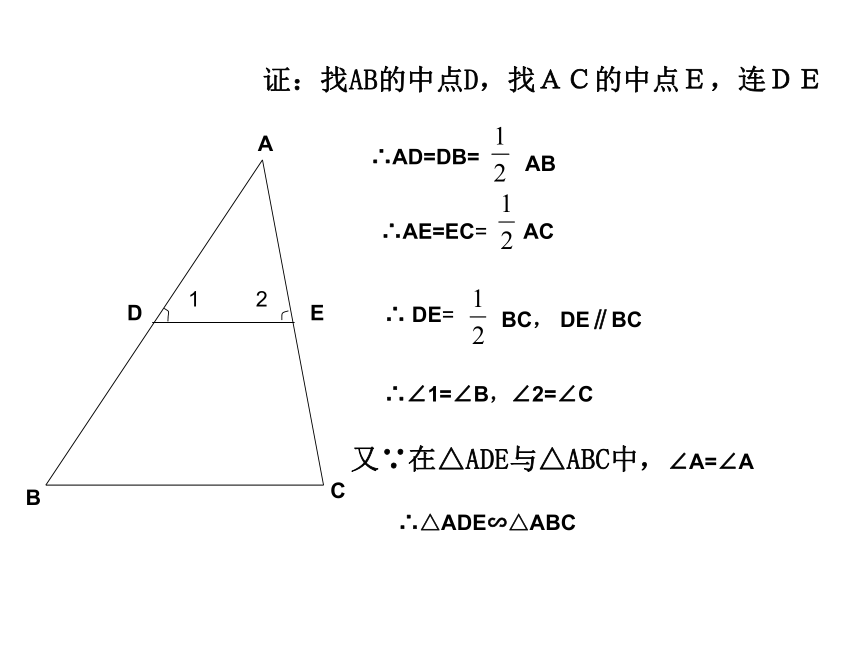
又∵在△ADE与△ABC中,∠A=∠A
∴∠1=∠B,∠2=∠C
∴AD=DB=
AB
∴AE=EC=
AC
∴ DE=
BC, DE∥BC
∴△ADE∽△ABC
A
B
C
D
E
2
1
证:找AB的中点D,找AC的中点E,连DE
那我们知道这样做出的三角形和原三角形相似,我们是取的AB的中点D来作中位线DE分割的。如果我们任意在AB上取点来作BC的平行线所得三角形也和原三角形相似吗?请大家在AB上任取点
D,过D作BC的平行线,交AC于E,量出各对应边的长度,并计算对应边的比。
A
B
C
D
E
D
预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似
A
B
C
预备定理:平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似。
D
E
A
B
C
E
D
或两边延长线
1、四边形ABCD是平行四边形,则图中与△DEF 相似的三角形共有( )
B
试一试,我能行
2、在平行四边形ABCD中,EF∥AB, ,EF=4,
则CD的长为————
10
D
E
A
F
B
C
3、已知 AB∥ CD,AD、BC 交于点O,AO=2,DO=3,CD=6,
AB=————
A
C
B
D
O
4
A.1个 B.2个 C.3个 D.4个
A
B
C
D
E
身高DE =1.6m,
人的影子长度AD =0.8m
树的影子长度AB =4m,
树的高度BC = ?m
∵DE∥BC ∴△ADE∽△ABC
∴
∴
∴ h=8m
A
E
C
B
D
解:(1) ∵DE//BC, ∴ △ADE∽ △ABC
∴
又∵AB=8,AC=6,AD=8-2x,AE=y,
∴
∵0≤AD≤8 ∴0≤8-2X≤8 ∴0≤x≤4
(2)
∴当x=2时,S有最大值,且最大值是6。
∴
7、(江西中考题)如图,在Rt △ABC中, ∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度,过点D作DE//BC交AC于点E,设动点D运动的时间为x秒,AE的长为y。
(1)求出y与x的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时, △BDE的面积S有最大值,最大值为多少?
2
+6
2
A
E
C
B
D
求三角形
的边或角方法?
找它的全等
三角形
找它的相似
三角形
找到了后
利用相似三角形的性质:
对应角相等,对应边的比
相等
其他的判定定理
预备定理
定 义
收获成果
……..
作业:
1、课本P55复习巩固第5题;
2、课本P56综合运用第10题;
3、课本P57拓广探索第16题。
谢谢大家
再见!
想一想
树的高度
池塘的宽度
右边的四个三角形中,有一个是三角形1在放大镜中看到的图像,
请你把它找出来?
三角形1和三角形4有什么关系?
相似
1
找一找
5
2
3
4
A
B
C
△ABC∽△
K=1 时,
△ABC和△ 是
什么关系?
△ABC≌△
全等三角形的相似比为1,说明了全等三角形是相似三角形的特殊情况。
∠A=∠ , ∠B=∠ , ∠C=∠
我们有一块大的三角形的木板,现在我们要用它来做一小的三角形,这个小三角形的一边长是AB的一半,一边长是AC的一半。动动脑筋,我们该怎么做?请你画出来。
动手动脑
A
B
C
D
E
A
B
C
我们先找到AB的中点D,再找AC的中点E,连DE,得
到△ADE
那△ADE与△ABC有什么关系?
相似,那我们怎么来证明?
相似的定义来证
又∵在△ADE与△ABC中,∠A=∠A
∴∠1=∠B,∠2=∠C
∴AD=DB=
AB
∴AE=EC=
AC
∴ DE=
BC, DE∥BC
∴△ADE∽△ABC
A
B
C
D
E
2
1
证:找AB的中点D,找AC的中点E,连DE
那我们知道这样做出的三角形和原三角形相似,我们是取的AB的中点D来作中位线DE分割的。如果我们任意在AB上取点来作BC的平行线所得三角形也和原三角形相似吗?请大家在AB上任取点
D,过D作BC的平行线,交AC于E,量出各对应边的长度,并计算对应边的比。
A
B
C
D
E
D
预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似
A
B
C
预备定理:平行于三角形一边的直线和其他两边相交,所构成
的三角形与原三角形相似。
D
E
A
B
C
E
D
或两边延长线
1、四边形ABCD是平行四边形,则图中与△DEF 相似的三角形共有( )
B
试一试,我能行
2、在平行四边形ABCD中,EF∥AB, ,EF=4,
则CD的长为————
10
D
E
A
F
B
C
3、已知 AB∥ CD,AD、BC 交于点O,AO=2,DO=3,CD=6,
AB=————
A
C
B
D
O
4
A.1个 B.2个 C.3个 D.4个
A
B
C
D
E
身高DE =1.6m,
人的影子长度AD =0.8m
树的影子长度AB =4m,
树的高度BC = ?m
∵DE∥BC ∴△ADE∽△ABC
∴
∴
∴ h=8m
A
E
C
B
D
解:(1) ∵DE//BC, ∴ △ADE∽ △ABC
∴
又∵AB=8,AC=6,AD=8-2x,AE=y,
∴
∵0≤AD≤8 ∴0≤8-2X≤8 ∴0≤x≤4
(2)
∴当x=2时,S有最大值,且最大值是6。
∴
7、(江西中考题)如图,在Rt △ABC中, ∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度,过点D作DE//BC交AC于点E,设动点D运动的时间为x秒,AE的长为y。
(1)求出y与x的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时, △BDE的面积S有最大值,最大值为多少?
2
+6
2
A
E
C
B
D
求三角形
的边或角方法?
找它的全等
三角形
找它的相似
三角形
找到了后
利用相似三角形的性质:
对应角相等,对应边的比
相等
其他的判定定理
预备定理
定 义
收获成果
……..
作业:
1、课本P55复习巩固第5题;
2、课本P56综合运用第10题;
3、课本P57拓广探索第16题。
谢谢大家
再见!
