山东省冠县武训高中2011-2012学年高二上学期期中考试数学试题
文档属性
| 名称 | 山东省冠县武训高中2011-2012学年高二上学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 183.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-12-31 12:34:09 | ||
图片预览


文档简介
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共120分,考试时间100分钟.
第I卷(选择题 共48分)
一. 选择题(共12小题,每小题4分,共48分.在每小题列出的四个选项中,只有一项是符合题目要求的)
1.设,且,则下列结论中正确的是( )
A. B. C. D.
2.在△ABC中,(、b、c分别为角A、B、C的对边),则△ABC的形状为 ( )
A.正三角形 B.直角三角形
C.等腰三角形或直角三角形 D.等腰直角三角形
3..设是的面积,的对边分别为,且 则( )
A.是钝角三角形 B.是锐角三角形
C.可能为钝角三角形,也可能为锐角三角形 D.无法判断
4.设为等差数列,则下列数列中,成等差数列的个数为( )
① ② ③ ④(p、q为非零常数)
A.1 B.2 C.3 D.4
5.在△ABC中,A、B、C分别为a、b、c所对的角,若a、b、c成等差数列,则B的范围是( )
A.0<B≤ B.0<B≤ C.0<B≤ D. <B<π
两个等差数列和,其前项和分别为,且则等于( )
A. B. C. D.
7.不等式组 表示的平面区域是 ( )
A. 矩形 B. 三角形 C. 直角梯形 D. 等腰梯形
8.等差数列中,,,则此数列前项和等于( )
A. B. C. D.
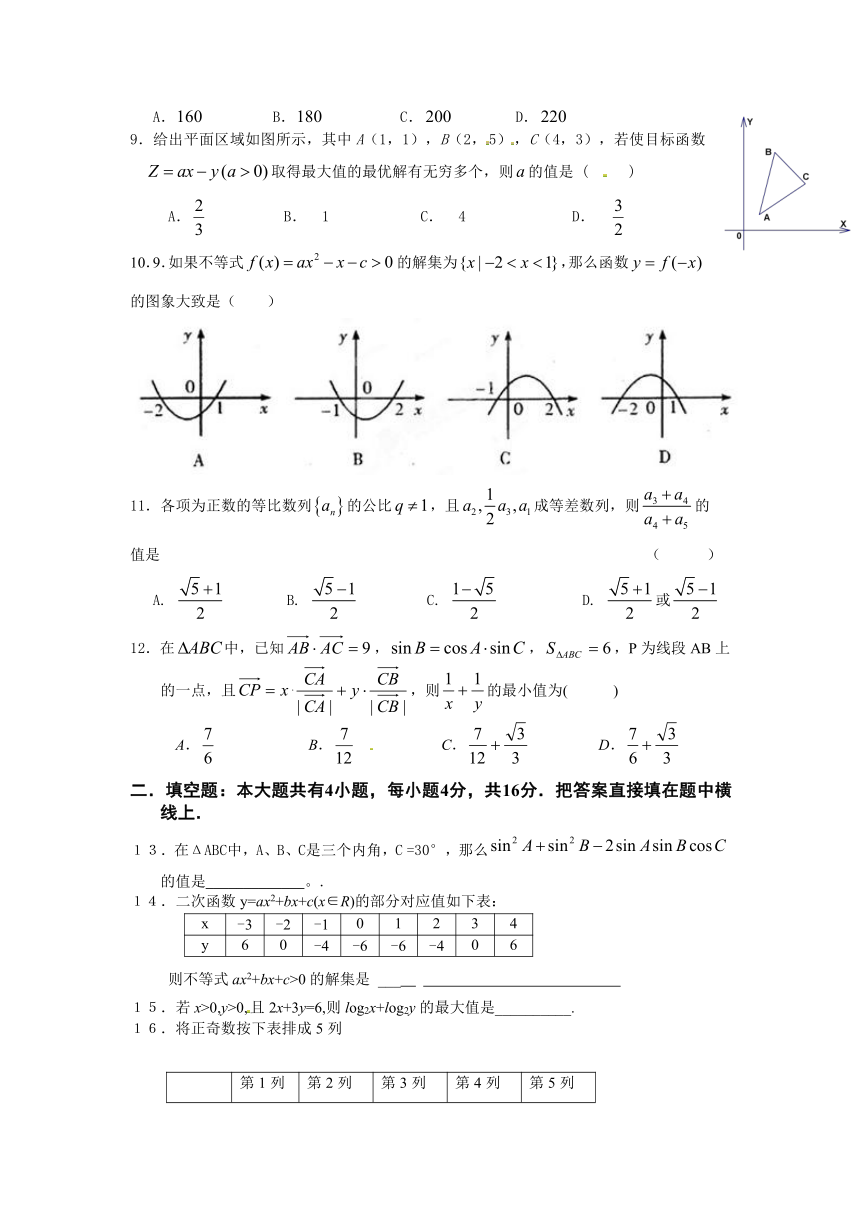
9.给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3),若使目标函数取得最大值的最优解有无穷多个,则的值是 ( )
A. B. 1 C. 4 D.
10.9.如果不等式的解集为,那么函数的图象大致是( )
11.各项为正数的等比数列的公比,且成等差数列,则的
值是 ( )
A. B. C. D. 或
12.在中,已知,, ( http: / / www. / ),P为线段AB上的一点,且.,则的最小值为( )
A. B. C. D.
二.填空题:本大题共有4小题,每小题4分,共16分.把答案直接填在题中横线上.
13.在ΔABC中,A、B、C是三个内角,C =30°,那么的值是_____________。.
14.二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
x -3 -2 -1 0 1 2 3 4
y 6 0 -4 -6 -6 -4 0 6
则不等式ax2+bx+c>0的解集是 ___
15.若x>0,y>0,且2x+3y=6,则log2x+log2y的最大值是__________.
16.将正奇数按下表排成5列
第1列 第2列 第3列 第4列 第5列
第1行 1 3 5 7
第2行 15 13 11 9
第3行 17 19 21 23
那么,2011应在第 ___________行_________列.
三、解答题:(本大题共5小题,共56分,解答应写出文字说明,证明过程或演算步骤)
17,(本小题满分10分)已知A、B、C为△ABC的三内角,且其对边分别为a、b、c. 若, , 且·=.
⑴ 求角A的大小;
⑵ 若a=2,三角形面积S=,求b+c的值.
18,(本小题满分10分)已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别是一个等比数列的第二项、第三项、第四项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设=(n∈N*),=b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有总成立?若存在,求出t;若不存在,请说明理由
19, (本小题满分12分) 已知二次函数的二次项系数为,且不等式的解集为(1,3)。
(1)若方程有两个相等的实数根,求的解析式;
(2)若的最大值为正数,求的取值范围。
20.(本小题满分12分)一缉私艇发现在北偏东方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东的方向去追,.求追及所需的时间和角的正弦值.
22,(本小题满分12分)已知数列的前项和为,且是与2的等差中项,数列中,,点在直线上.
⑴求和的值;
⑵求数列的通项和;
⑶ 设,求数列的前n项和.
参考答案
S△ABC=bc·sinA=b·c·sin =,∴bc=4, ……6分
又由余弦定理得:a2=b2+c2-2bc·cos120°=b2+c2+bc , ……8分
∴16=(b+c)2,故b+c=4. ……………………………10分
18.解:(Ⅰ)由题意得(a1+d)(a1+13d)=(a1+4d)2, ……………… 2 分
整理得2a1d=d2.
∵a1=1,解得(d=0舍),d=2. ………………………………………… 4 分
∴an=2n-1(n∈N*). …………………………………………………… 5 分
(Ⅱ)bn===(-),
∴Sn=b1+b2+…+bn=[(1-)+(-)+…+(-)]
=(1-)=. …………………………………… 8 分
假设存在整数t满足Sn>总成立.
又Sn+1-Sn=-=>0,
∴数列{Sn}是单调递增的.
∴S1=为Sn的最小值,故<,即t<9.
∵t∈N*,
∴适合条件的t的最大值为8. ……………………………… 10分
19.解:(1)依题意可设f(x)+2x=a(x-1)(x-3),且a<0 …………… 2分
∴f(x)= a(x-1)(x-3)-2x
由f(x)+6a=0有两个相等的实数根,
即方程ax2-(2+4a)x+9a=0有两个相等的实数根,
∴△=0
∴a=1,a=- …………………4分
∵a<0
∴f(x)=。 …………………6分
(2)f(x)= a(x-1)(x-3)-2x=a(x- 且a<0 ……8分
∴ …………………10分
解之得:∴a的取值范围为 ………12分
20. 解: 设A,C分别表示缉私艇,走私船的位置,设经过 小时后在B处追上, ……2分
则有
由余弦定理可得:
……8分
……10分
∴
答:所以所需时间2小时, ……12分
21.解:(1)∵是与2的等差中项
∴ --------------------------------------------1分
∴
-------------------------3分
(2)
.
∵a1=2 ∴ ------------------------------------6分
∴ -----------8分
第I卷(选择题 共48分)
一. 选择题(共12小题,每小题4分,共48分.在每小题列出的四个选项中,只有一项是符合题目要求的)
1.设,且,则下列结论中正确的是( )
A. B. C. D.
2.在△ABC中,(、b、c分别为角A、B、C的对边),则△ABC的形状为 ( )
A.正三角形 B.直角三角形
C.等腰三角形或直角三角形 D.等腰直角三角形
3..设是的面积,的对边分别为,且 则( )
A.是钝角三角形 B.是锐角三角形
C.可能为钝角三角形,也可能为锐角三角形 D.无法判断
4.设为等差数列,则下列数列中,成等差数列的个数为( )
① ② ③ ④(p、q为非零常数)
A.1 B.2 C.3 D.4
5.在△ABC中,A、B、C分别为a、b、c所对的角,若a、b、c成等差数列,则B的范围是( )
A.0<B≤ B.0<B≤ C.0<B≤ D. <B<π
两个等差数列和,其前项和分别为,且则等于( )
A. B. C. D.
7.不等式组 表示的平面区域是 ( )
A. 矩形 B. 三角形 C. 直角梯形 D. 等腰梯形
8.等差数列中,,,则此数列前项和等于( )
A. B. C. D.
9.给出平面区域如图所示,其中A(1,1),B(2,5),C(4,3),若使目标函数取得最大值的最优解有无穷多个,则的值是 ( )
A. B. 1 C. 4 D.
10.9.如果不等式的解集为,那么函数的图象大致是( )
11.各项为正数的等比数列的公比,且成等差数列,则的
值是 ( )
A. B. C. D. 或
12.在中,已知,, ( http: / / www. / ),P为线段AB上的一点,且.,则的最小值为( )
A. B. C. D.
二.填空题:本大题共有4小题,每小题4分,共16分.把答案直接填在题中横线上.
13.在ΔABC中,A、B、C是三个内角,C =30°,那么的值是_____________。.
14.二次函数y=ax2+bx+c(x∈R)的部分对应值如下表:
x -3 -2 -1 0 1 2 3 4
y 6 0 -4 -6 -6 -4 0 6
则不等式ax2+bx+c>0的解集是 ___
15.若x>0,y>0,且2x+3y=6,则log2x+log2y的最大值是__________.
16.将正奇数按下表排成5列
第1列 第2列 第3列 第4列 第5列
第1行 1 3 5 7
第2行 15 13 11 9
第3行 17 19 21 23
那么,2011应在第 ___________行_________列.
三、解答题:(本大题共5小题,共56分,解答应写出文字说明,证明过程或演算步骤)
17,(本小题满分10分)已知A、B、C为△ABC的三内角,且其对边分别为a、b、c. 若, , 且·=.
⑴ 求角A的大小;
⑵ 若a=2,三角形面积S=,求b+c的值.
18,(本小题满分10分)已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别是一个等比数列的第二项、第三项、第四项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设=(n∈N*),=b1+b2+…+bn,是否存在最大的整数t,使得任意的n均有总成立?若存在,求出t;若不存在,请说明理由
19, (本小题满分12分) 已知二次函数的二次项系数为,且不等式的解集为(1,3)。
(1)若方程有两个相等的实数根,求的解析式;
(2)若的最大值为正数,求的取值范围。
20.(本小题满分12分)一缉私艇发现在北偏东方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东的方向去追,.求追及所需的时间和角的正弦值.
22,(本小题满分12分)已知数列的前项和为,且是与2的等差中项,数列中,,点在直线上.
⑴求和的值;
⑵求数列的通项和;
⑶ 设,求数列的前n项和.
参考答案
S△ABC=bc·sinA=b·c·sin =,∴bc=4, ……6分
又由余弦定理得:a2=b2+c2-2bc·cos120°=b2+c2+bc , ……8分
∴16=(b+c)2,故b+c=4. ……………………………10分
18.解:(Ⅰ)由题意得(a1+d)(a1+13d)=(a1+4d)2, ……………… 2 分
整理得2a1d=d2.
∵a1=1,解得(d=0舍),d=2. ………………………………………… 4 分
∴an=2n-1(n∈N*). …………………………………………………… 5 分
(Ⅱ)bn===(-),
∴Sn=b1+b2+…+bn=[(1-)+(-)+…+(-)]
=(1-)=. …………………………………… 8 分
假设存在整数t满足Sn>总成立.
又Sn+1-Sn=-=>0,
∴数列{Sn}是单调递增的.
∴S1=为Sn的最小值,故<,即t<9.
∵t∈N*,
∴适合条件的t的最大值为8. ……………………………… 10分
19.解:(1)依题意可设f(x)+2x=a(x-1)(x-3),且a<0 …………… 2分
∴f(x)= a(x-1)(x-3)-2x
由f(x)+6a=0有两个相等的实数根,
即方程ax2-(2+4a)x+9a=0有两个相等的实数根,
∴△=0
∴a=1,a=- …………………4分
∵a<0
∴f(x)=。 …………………6分
(2)f(x)= a(x-1)(x-3)-2x=a(x- 且a<0 ……8分
∴ …………………10分
解之得:∴a的取值范围为 ………12分
20. 解: 设A,C分别表示缉私艇,走私船的位置,设经过 小时后在B处追上, ……2分
则有
由余弦定理可得:
……8分
……10分
∴
答:所以所需时间2小时, ……12分
21.解:(1)∵是与2的等差中项
∴ --------------------------------------------1分
∴
-------------------------3分
(2)
.
∵a1=2 ∴ ------------------------------------6分
∴ -----------8分
同课章节目录
