2020-2021九年级数学下册 第二十七章 相似 单元测试题(Word版 含答案)
文档属性
| 名称 | 2020-2021九年级数学下册 第二十七章 相似 单元测试题(Word版 含答案) | 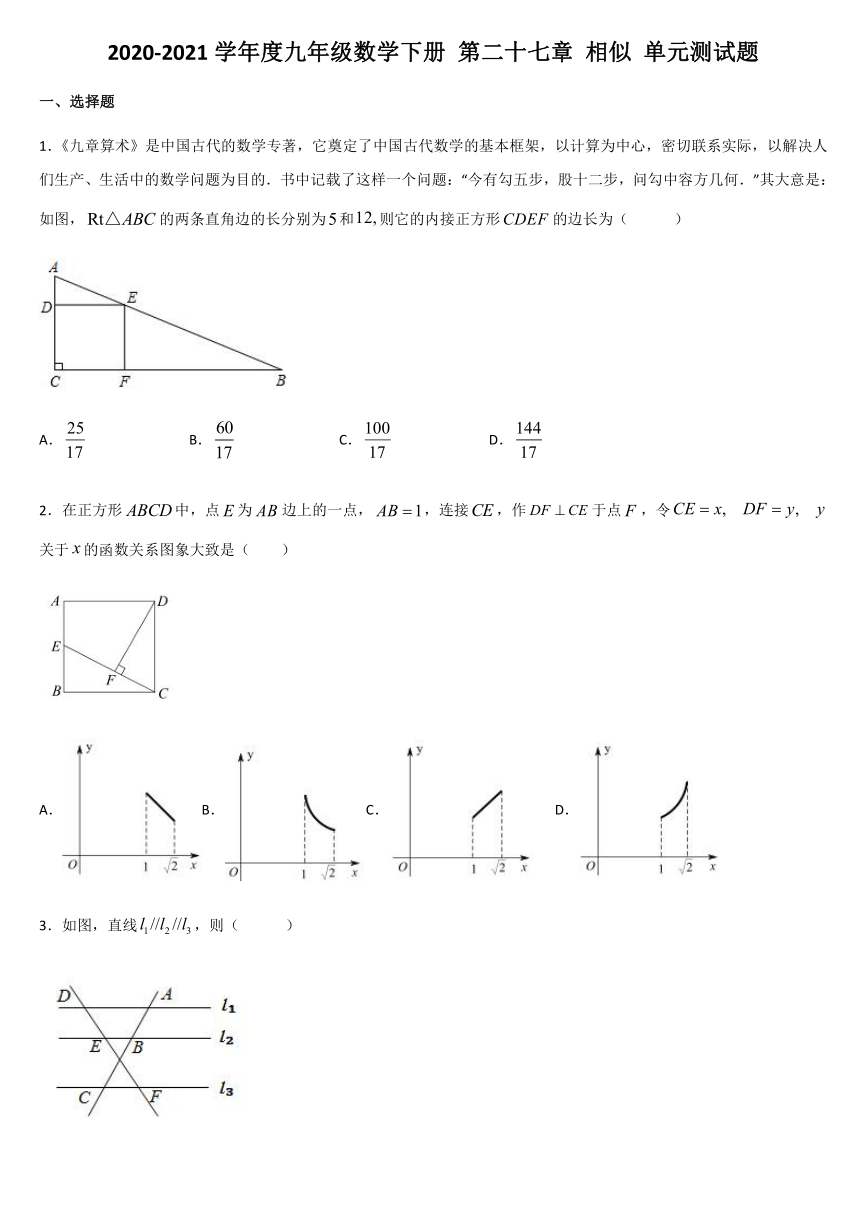 | |
| 格式 | zip | ||
| 文件大小 | 789.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 10:11:36 | ||
图片预览

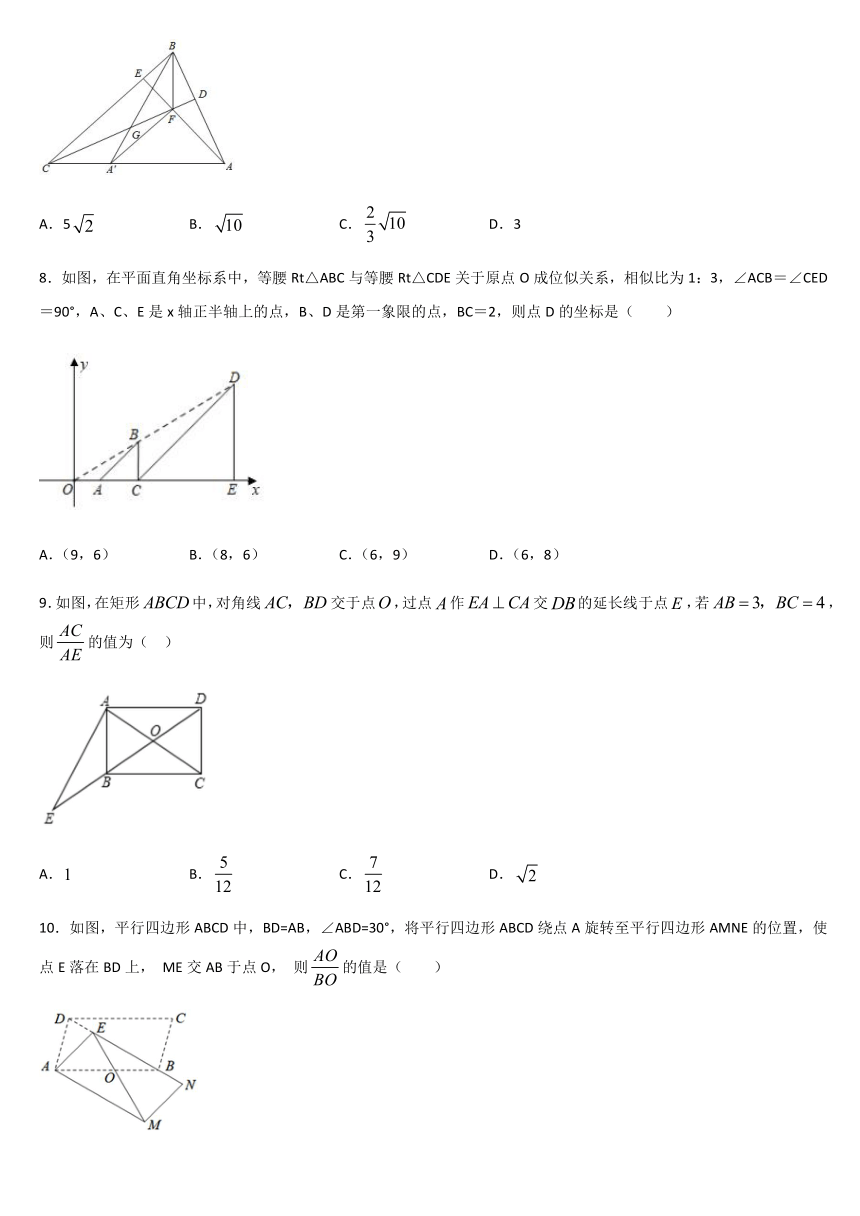
文档简介
2020-2021学年度九年级数学下册
第二十七章
相似
单元测试题
一、选择题
1.《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何.”其大意是:如图,的两条直角边的长分别为和则它的内接正方形的边长为( )
A.
B.
C.
D.
2.在正方形中,点为边上的一点,,连接,作于点,令关于的函数关系图象大致是(
)
A.B.C.
D.
3.如图,直线,则( )
A.
B.
C.
D.
4.如图,在平面直角坐标系中,已知与是位似图形,原点是位似中心,位似比,若,则的长为(
).
A.5
B.6
C.9
D.12
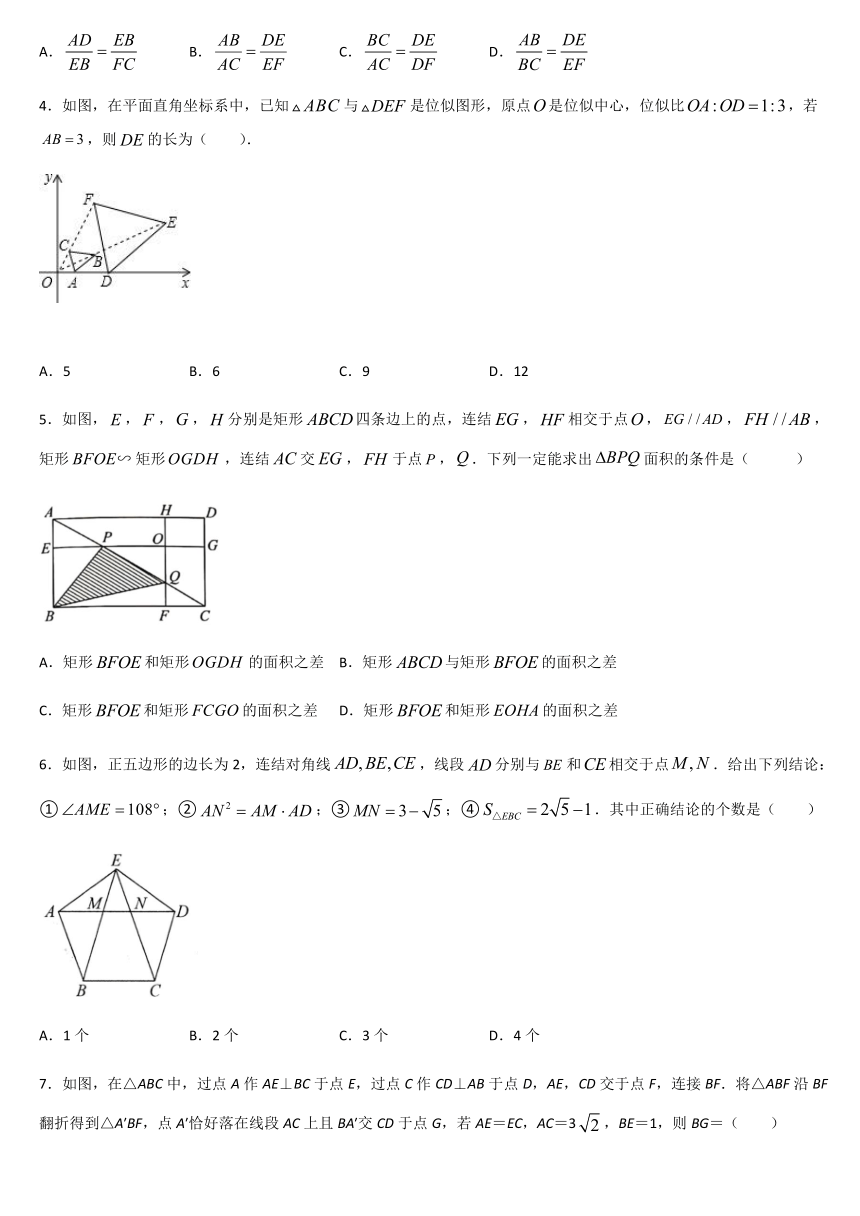
5.如图,,,,分别是矩形四条边上的点,连结,相交于点,,,矩形矩形,连结交,于点,.下列一定能求出面积的条件是(
)
A.矩形和矩形的面积之差
B.矩形与矩形的面积之差
C.矩形和矩形的面积之差
D.矩形和矩形的面积之差
6.如图,正五边形的边长为2,连结对角线,线段分别与和相交于点.给出下列结论:①;②;③;④.其中正确结论的个数是(
)
A.1个
B.2个
C.3个
D.4个
7.如图,在△ABC中,过点A作AE⊥BC于点E,过点C作CD⊥AB于点D,AE,CD交于点F,连接BF.将△ABF沿BF翻折得到△A′BF,点A′恰好落在线段AC上且BA′交CD于点G,若AE=EC,AC=3,BE=1,则BG=( )
A.5
B.
C.
D.3
8.如图,在平面直角坐标系中,等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系,相似比为1:3,∠ACB=∠CED=90°,A、C、E是x轴正半轴上的点,B、D是第一象限的点,BC=2,则点D的坐标是( )
A.(9,6)
B.(8,6)
C.(6,9)
D.(6,8)
9.如图,在矩形中,对角线交于点,过点作交的延长线于点,若,则的值为(
)
A.
B.
C.
D.
10.如图,平行四边形ABCD中,BD=AB,∠ABD=30°,将平行四边形ABCD绕点A旋转至平行四边形AMNE的位置,使点E落在BD上,
ME交AB于点O,
则的值是(
)
A.
B.
C.
D.
二、填空题
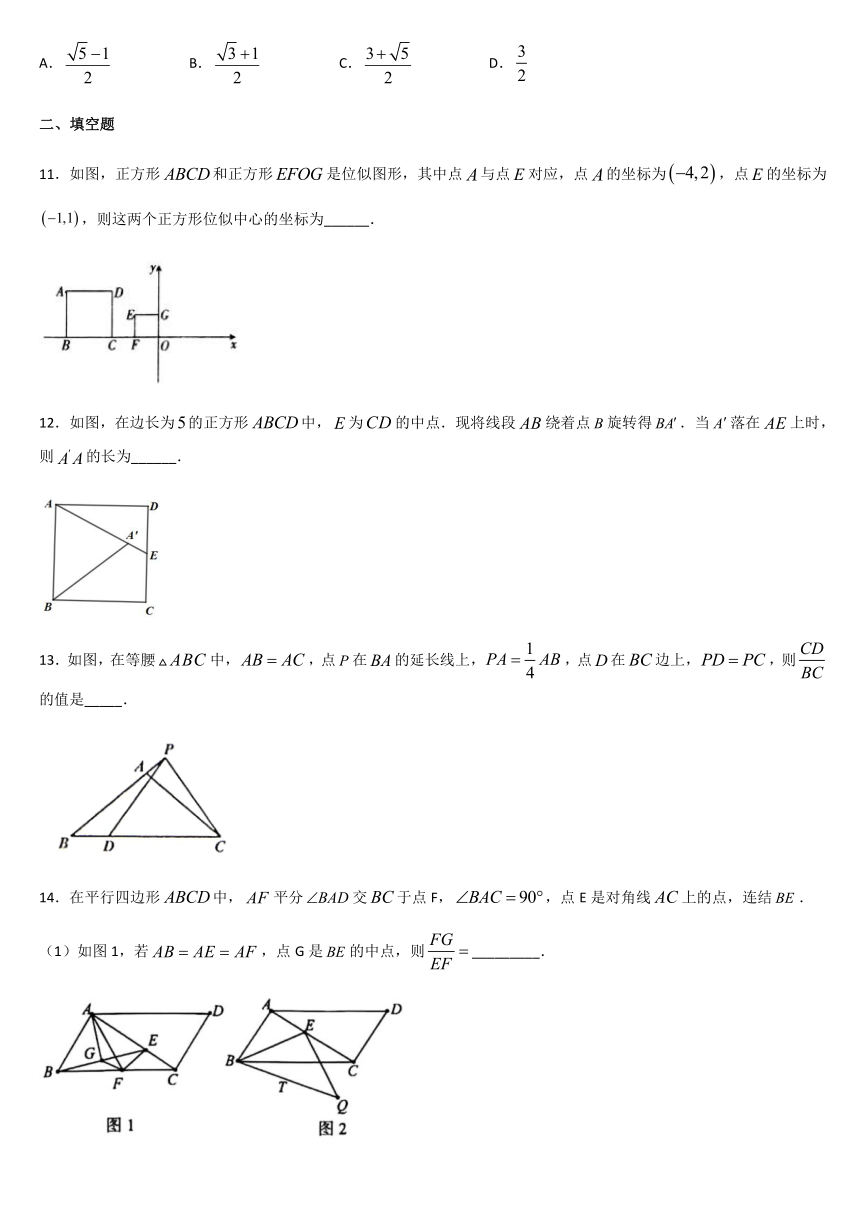
11.如图,正方形和正方形是位似图形,其中点与点对应,点的坐标为,点的坐标为,则这两个正方形位似中心的坐标为______.
12.如图,在边长为的正方形中,为的中点.现将线段绕着点旋转得.当落在上时,则的长为______.
13.如图,在等腰中,,点在的延长线上,,点在边上,,则的值是_____.
14.在平行四边形中,平分交于点F,,点E是对角线上的点,连结.
(1)如图1,若,点G是的中点,则_________.
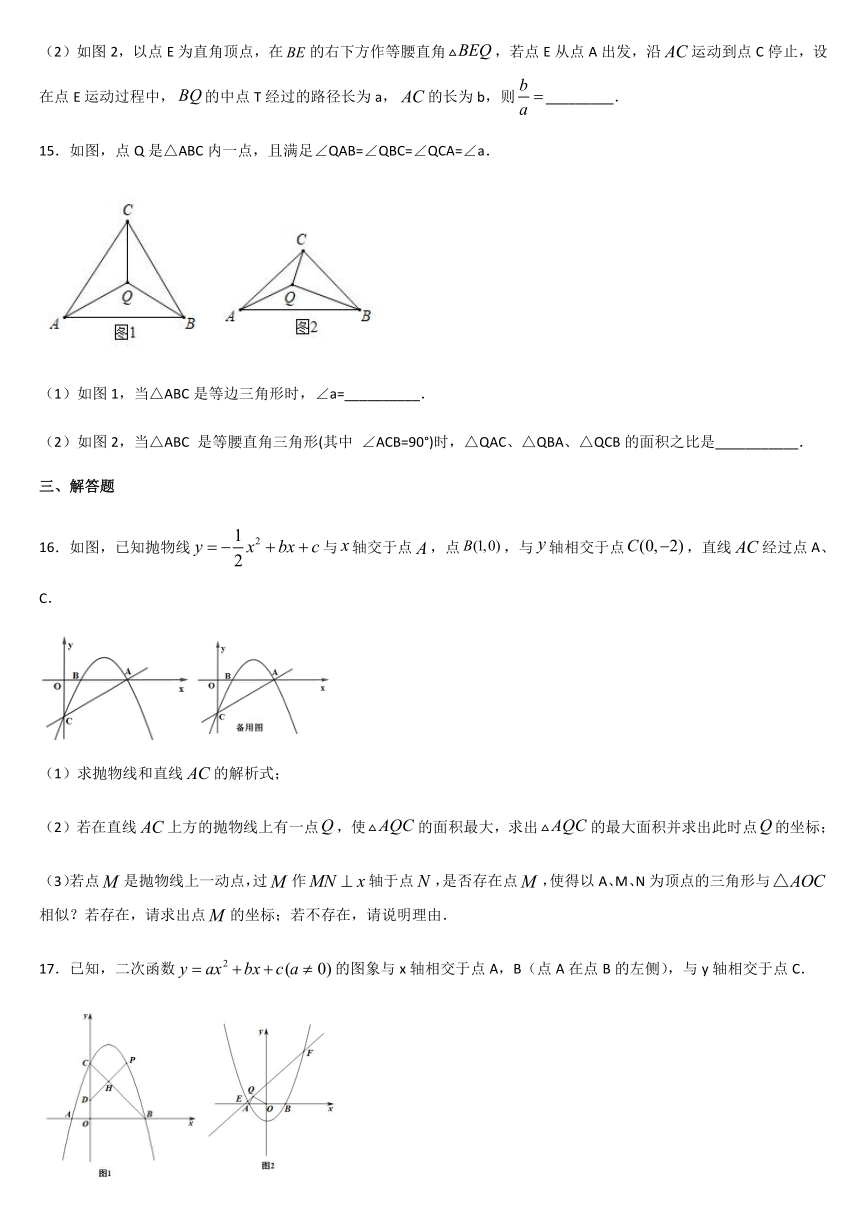
(2)如图2,以点E为直角顶点,在的右下方作等腰直角,若点E从点A出发,沿运动到点C停止,设在点E运动过程中,的中点T经过的路径长为a,的长为b,则_________.
15.如图,点Q是△ABC内一点,且满足∠QAB=∠QBC=∠QCA=∠a.
(1)如图1,当△ABC是等边三角形时,∠a=__________.
(2)如图2,当△ABC
是等腰直角三角形(其中
∠ACB=90°)时,△QAC、△QBA、△QCB的面积之比是___________.
三、解答题
16.如图,已知抛物线与轴交于点,点,与轴相交于点,直线经过点A、C.
(1)求抛物线和直线的解析式;
(2)若在直线上方的抛物线上有一点,使的面积最大,求出的最大面积并求出此时点的坐标;
(3)若点是抛物线上一动点,过作轴于点,是否存在点,使得以A、M、N为顶点的三角形与相似?若存在,请求出点的坐标;若不存在,请说明理由.
17.已知,二次函数的图象与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C.
(1)若,如图1,已知A,C两点的坐标为.
①求抛物线的解析式,并求出B的坐标.
②点P是抛物线上第一象限内一个动点.y轴上有一点,连结交于点H,若H恰好平分,求点P的坐标.
(2)若,,,,如图2,抛物线与一次函数的图象交于E,F两点,点E在点F的左侧.在直线上是否存在唯一一点Q,使得?若存在,请求出此时k的值;若不存在,请说明理由.
18.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ是等腰三角形;
(3)试探究t为何值时,CP=CQ;
(4)连接AQ,CP,若AQ⊥CP,求t的值.
19.(探索发现)如图①,是一张直角三角形纸片,,小明想从中剪出一个以为内角且面积最大的矩形,经过多次操作发现,当沿着中位线剪下时,矩形的面积最大,经证明发现:矩形的最大面积与原三角形面积的比值为__________.
(拓展应用)
如图②,在中,,边上的高,矩形的顶点分别在边上,顶点在边上,则矩形面积的最大值为__________.(用含的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形”,小明从中剪出了一个面积最大的矩形(为所剪出矩形的内角),求该矩形的面积.
(实际应用)
如图④,现有一块四边形的木板余料,经测量,且,木匠徐师傅从这块余料中裁出了顶点在边上且面积最大的矩形,求该矩形的面积.
20.如图,抛物线与x轴交于A,B两点,与y轴交于C点,且点A(-1,0).
(1)求抛物线的解析式及顶点D
的坐标;
(2)判断的形状,并证明你的结论;
(3)点是轴上的一个动点,
①当的值最小时,
;
②过点作轴,交抛物线于点,连接,面积的最大值为
;
(4)为坐标轴上一点,在平面内是否存在点,使以为顶点的四边形为矩形?若存在,请直接写出点的坐标;若不存在,请说明理由.
21.在平面直角坐标系中,直线过点且与轴平行,直线过点且与轴平行,直线与直线相交于点.点为直线上一动点,反比例函数()的图象过点与直线相交于点.
(1)若点与点重合,求的值;
(2)若,是否存在点及轴上的点,使得以点、、为顶点的三角形与全等?若存在,求点坐标:若不存在,请说明理由.
(3)连接、、,且的面积为面积的2倍?求点的坐标.
22.如图1,在平面直角坐标系中,直线y=?2x+6交坐标轴于A,B两点,过点C(-6,0)作CD交AB于D,交y轴于点E,且△COE
≌△BOA.
(1)求点B的坐标,线段OA的长;
(2)确定直线CD的解析式,求点D的坐标;
(3)如图2,点M是线段CE上一动点(不与点C,E重合),ON⊥OM交AB于点N,连接MN,当△OMN的面积最小时,请求点M的坐标和△OMN的面积.
(4)如图3,点M是直线CD上一动点,过点M作x轴的垂线,交轴于点Q,连接EQ,若∠EQM=∠ACD,求点M的坐标.
23.(1)观察猜想:
如图1,在中,,点D,E分别在边,上,,,将绕点A逆时针旋转到如图2所示的位置,连接,交于点G,连接交于点F,则值为______,的度数为_____.
(2)类比探究:
如图3,当,时,请求出的值及的度数.
(3)拓展应用:
如图4,在四边形中,,,.若,,请直接写出A,D两点之间的距离.
【参考答案】
1.B
2.B
3.D
4.C
5.A
6.C
7.C
8.A
9.C
10.B
11.
12.
13.
14.(1)
(2)
15.30°
1:2:2
16.(1);;(2)的面积最大为4,此时;(3)存在,.
17.(1)①,;②或;(2)存在,或
18.(1)1或;(2)或或;(3);(4).
19.【探索发现】;【拓展应用】;【灵活应用】720;【实际应用】
20.(1),顶点的坐标为;(2)直角三角形,证明略;(3)①;②4;(4)存在,点Q的坐标为(,)或(,)或(,).
21.(1);(2)存在,点坐标为;(3)点坐标为或.
22.(1)(0,6),3;(2)();(3)(,),;(4)(,),(,).
23.(1),45°;(2),30°;(3)2
第二十七章
相似
单元测试题
一、选择题
1.《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何.”其大意是:如图,的两条直角边的长分别为和则它的内接正方形的边长为( )
A.
B.
C.
D.
2.在正方形中,点为边上的一点,,连接,作于点,令关于的函数关系图象大致是(
)
A.B.C.
D.
3.如图,直线,则( )
A.
B.
C.
D.
4.如图,在平面直角坐标系中,已知与是位似图形,原点是位似中心,位似比,若,则的长为(
).
A.5
B.6
C.9
D.12
5.如图,,,,分别是矩形四条边上的点,连结,相交于点,,,矩形矩形,连结交,于点,.下列一定能求出面积的条件是(
)
A.矩形和矩形的面积之差
B.矩形与矩形的面积之差
C.矩形和矩形的面积之差
D.矩形和矩形的面积之差
6.如图,正五边形的边长为2,连结对角线,线段分别与和相交于点.给出下列结论:①;②;③;④.其中正确结论的个数是(
)
A.1个
B.2个
C.3个
D.4个
7.如图,在△ABC中,过点A作AE⊥BC于点E,过点C作CD⊥AB于点D,AE,CD交于点F,连接BF.将△ABF沿BF翻折得到△A′BF,点A′恰好落在线段AC上且BA′交CD于点G,若AE=EC,AC=3,BE=1,则BG=( )
A.5
B.
C.
D.3
8.如图,在平面直角坐标系中,等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系,相似比为1:3,∠ACB=∠CED=90°,A、C、E是x轴正半轴上的点,B、D是第一象限的点,BC=2,则点D的坐标是( )
A.(9,6)
B.(8,6)
C.(6,9)
D.(6,8)
9.如图,在矩形中,对角线交于点,过点作交的延长线于点,若,则的值为(
)
A.
B.
C.
D.
10.如图,平行四边形ABCD中,BD=AB,∠ABD=30°,将平行四边形ABCD绕点A旋转至平行四边形AMNE的位置,使点E落在BD上,
ME交AB于点O,
则的值是(
)
A.
B.
C.
D.
二、填空题
11.如图,正方形和正方形是位似图形,其中点与点对应,点的坐标为,点的坐标为,则这两个正方形位似中心的坐标为______.
12.如图,在边长为的正方形中,为的中点.现将线段绕着点旋转得.当落在上时,则的长为______.
13.如图,在等腰中,,点在的延长线上,,点在边上,,则的值是_____.
14.在平行四边形中,平分交于点F,,点E是对角线上的点,连结.
(1)如图1,若,点G是的中点,则_________.
(2)如图2,以点E为直角顶点,在的右下方作等腰直角,若点E从点A出发,沿运动到点C停止,设在点E运动过程中,的中点T经过的路径长为a,的长为b,则_________.
15.如图,点Q是△ABC内一点,且满足∠QAB=∠QBC=∠QCA=∠a.
(1)如图1,当△ABC是等边三角形时,∠a=__________.
(2)如图2,当△ABC
是等腰直角三角形(其中
∠ACB=90°)时,△QAC、△QBA、△QCB的面积之比是___________.
三、解答题
16.如图,已知抛物线与轴交于点,点,与轴相交于点,直线经过点A、C.
(1)求抛物线和直线的解析式;
(2)若在直线上方的抛物线上有一点,使的面积最大,求出的最大面积并求出此时点的坐标;
(3)若点是抛物线上一动点,过作轴于点,是否存在点,使得以A、M、N为顶点的三角形与相似?若存在,请求出点的坐标;若不存在,请说明理由.
17.已知,二次函数的图象与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C.
(1)若,如图1,已知A,C两点的坐标为.
①求抛物线的解析式,并求出B的坐标.
②点P是抛物线上第一象限内一个动点.y轴上有一点,连结交于点H,若H恰好平分,求点P的坐标.
(2)若,,,,如图2,抛物线与一次函数的图象交于E,F两点,点E在点F的左侧.在直线上是否存在唯一一点Q,使得?若存在,请求出此时k的值;若不存在,请说明理由.
18.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)试探究t为何值时,△BPQ是等腰三角形;
(3)试探究t为何值时,CP=CQ;
(4)连接AQ,CP,若AQ⊥CP,求t的值.
19.(探索发现)如图①,是一张直角三角形纸片,,小明想从中剪出一个以为内角且面积最大的矩形,经过多次操作发现,当沿着中位线剪下时,矩形的面积最大,经证明发现:矩形的最大面积与原三角形面积的比值为__________.
(拓展应用)
如图②,在中,,边上的高,矩形的顶点分别在边上,顶点在边上,则矩形面积的最大值为__________.(用含的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形”,小明从中剪出了一个面积最大的矩形(为所剪出矩形的内角),求该矩形的面积.
(实际应用)
如图④,现有一块四边形的木板余料,经测量,且,木匠徐师傅从这块余料中裁出了顶点在边上且面积最大的矩形,求该矩形的面积.
20.如图,抛物线与x轴交于A,B两点,与y轴交于C点,且点A(-1,0).
(1)求抛物线的解析式及顶点D
的坐标;
(2)判断的形状,并证明你的结论;
(3)点是轴上的一个动点,
①当的值最小时,
;
②过点作轴,交抛物线于点,连接,面积的最大值为
;
(4)为坐标轴上一点,在平面内是否存在点,使以为顶点的四边形为矩形?若存在,请直接写出点的坐标;若不存在,请说明理由.
21.在平面直角坐标系中,直线过点且与轴平行,直线过点且与轴平行,直线与直线相交于点.点为直线上一动点,反比例函数()的图象过点与直线相交于点.
(1)若点与点重合,求的值;
(2)若,是否存在点及轴上的点,使得以点、、为顶点的三角形与全等?若存在,求点坐标:若不存在,请说明理由.
(3)连接、、,且的面积为面积的2倍?求点的坐标.
22.如图1,在平面直角坐标系中,直线y=?2x+6交坐标轴于A,B两点,过点C(-6,0)作CD交AB于D,交y轴于点E,且△COE
≌△BOA.
(1)求点B的坐标,线段OA的长;
(2)确定直线CD的解析式,求点D的坐标;
(3)如图2,点M是线段CE上一动点(不与点C,E重合),ON⊥OM交AB于点N,连接MN,当△OMN的面积最小时,请求点M的坐标和△OMN的面积.
(4)如图3,点M是直线CD上一动点,过点M作x轴的垂线,交轴于点Q,连接EQ,若∠EQM=∠ACD,求点M的坐标.
23.(1)观察猜想:
如图1,在中,,点D,E分别在边,上,,,将绕点A逆时针旋转到如图2所示的位置,连接,交于点G,连接交于点F,则值为______,的度数为_____.
(2)类比探究:
如图3,当,时,请求出的值及的度数.
(3)拓展应用:
如图4,在四边形中,,,.若,,请直接写出A,D两点之间的距离.
【参考答案】
1.B
2.B
3.D
4.C
5.A
6.C
7.C
8.A
9.C
10.B
11.
12.
13.
14.(1)
(2)
15.30°
1:2:2
16.(1);;(2)的面积最大为4,此时;(3)存在,.
17.(1)①,;②或;(2)存在,或
18.(1)1或;(2)或或;(3);(4).
19.【探索发现】;【拓展应用】;【灵活应用】720;【实际应用】
20.(1),顶点的坐标为;(2)直角三角形,证明略;(3)①;②4;(4)存在,点Q的坐标为(,)或(,)或(,).
21.(1);(2)存在,点坐标为;(3)点坐标为或.
22.(1)(0,6),3;(2)();(3)(,),;(4)(,),(,).
23.(1),45°;(2),30°;(3)2
