高二数学模拟试题(理科)
图片预览
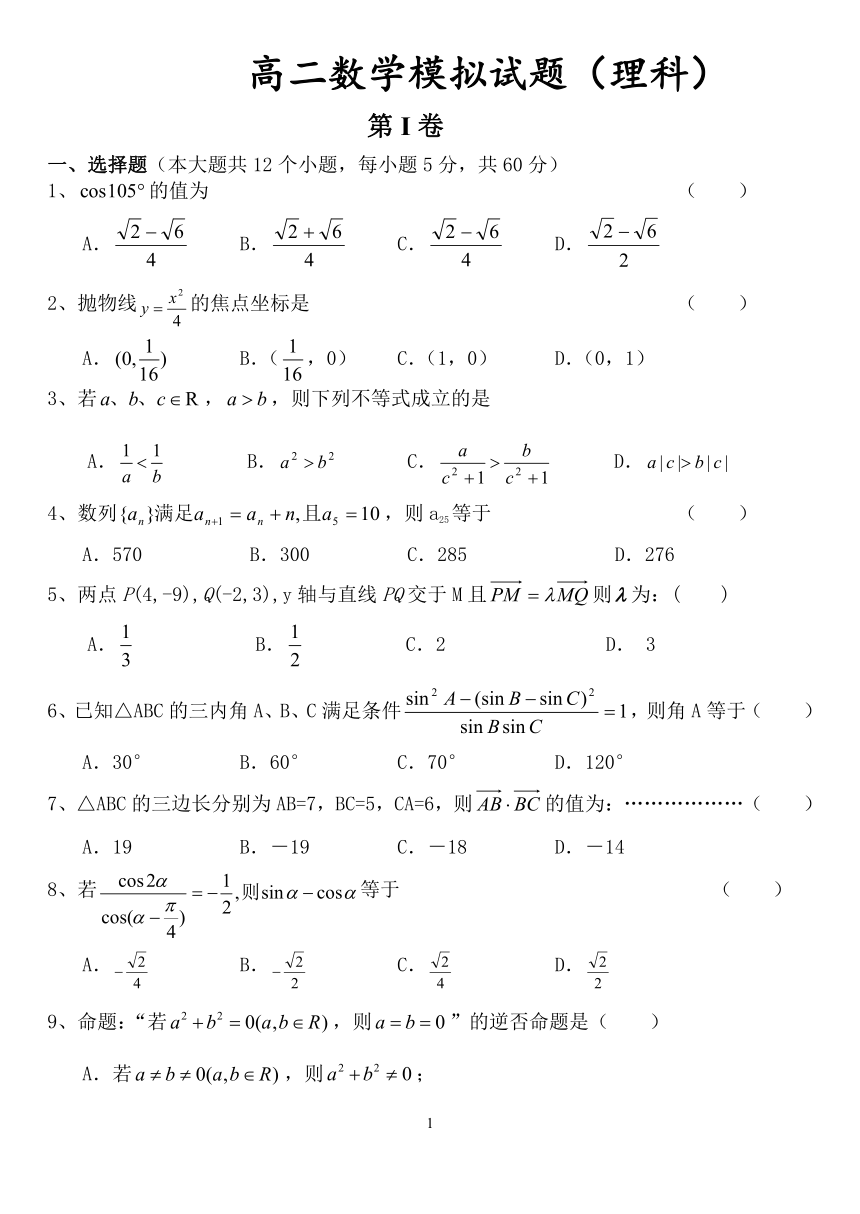



文档简介
高二数学模拟试题(理科)
第I卷
一、选择题(本大题共12个小题,每小题5分,共60分)
1、的值为 ( )
A. B. C. D.
2、抛物线的焦点坐标是 ( )
A. B.(,0) C.(1,0) D.(0,1)
3、若,,则下列不等式成立的是
A. B. C. D.
4、数列,则a25等于 ( )
A.570 B.300 C.285 D.276
5、两点P(4,-9),Q(-2,3),y轴与直线PQ交于M且则为:( )
A. B. C.2 D. 3
6、已知△ABC的三内角A、B、C满足条件,则角A等于( )
A.30° B.60° C.70° D.120°
7、△ABC的三边长分别为AB=7,BC=5,CA=6,则的值为:………………( )
A.19 B.-19 C.-18 D.-14
8、若等于 ( )
A. B. C. D.
9、命题:“若,则”的逆否命题是( )
若,则;
若,则;
若,则;
若,则;
10、在等比数列 ( )
A.-2 B.-2或2 C. D.
11、已知,则的最小值是
A. B. C. D.25
12、点在椭圆=1上且到直线的距离为,那么点的个数为 ( )
A.1 ; B.2 ; C.3 ; D.4;
二、填空题:(本大题共4个小题,每小题4分,共16分)将答案填在答题纸指定位置
13、命题“”的否定是:
14、已知cos=,且,则cos( )= .
15、已知数列,则该数列的通项公式为 .
16、椭圆的焦点、,P为椭圆上的一点,已知,则△的面积为 .
三、解答题:(本大题共6小题,共74分,解答应写出必要的文字说明、证明过程或演算步骤)
17、(12分)已知.
(1)求的值;
(2)求的值.
18、(12分)已知等差数列
(1)求数列的通项公式;
(2)记数列的前n项和记为Sn,求Sn.
19、(12分)某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米。
(1)若设休闲区的长米,求公园ABCD所占面积S关于的函数的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
20、(12分)已知向量
⑴;
⑵若
21、(12分)如图所示,一辆汽车从O点出发,沿海岸线一直线公路以100千米/小时的速度向东匀速行驶.汽车开动时,在距O点500千米,且与海岸线距离400千米的海面上M点处有一艘快艇与汽车同时出发,要把一件重要物品送给这辆汽车司机.该快艇至少以多大的速度行驶,才能将物品送到司机手中?并求出此时快艇行驶的方向.
(参考数据:)
22、(14分)已知椭圆C的中心在原点,焦点、在x轴上,点P为椭圆上的一个动点,且 的最大值为90°,直线过左焦点与椭圆交于A、B两点,的面积最大值为12.
(1)求椭圆C的离心率;(5分)
(2)求椭圆C的方程。(9分)
高二教学过程检测数学试题参考答案(理科)
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D C B C A B C D D B B
二、填空题:
13. 14. 15. 16. 9
三、解答题:
17、解:(1)
……………………2分
…………………………5分
(2)
=…………………………7分
…………………………10分
=-1……………………12分
18、解:(1)由题意得……………………2分
解得……………………4分
……………………6分
(2)由(1)得
……………………8分
……………………10分
……………………12分
19、解:⑴由,知
⑵
当且仅当时取等号
∴要使公园所占面积最小,休闲区A1B1C1D1的长为100米、宽为40米.
20、解:⑴
⑵(理科)
①当时,当县仅当时,取得最小值-1,这与已知矛盾;
②当时,取得最小值,由已知得
;
③当时,取得最小值,由已知得
解得,这与相矛盾,综上所述,为所求.
21、解:如图所示,设快艇从M处以v千米/小时的速
度出发,沿MN方向航行,t小时后在N点与汽
车相遇,MQ为M点到ON的距离,则MQ=400,
在△MON中,MO=500,ON=100t,MN=vt
设∠MON=,由题意知
……………………2分
由余弦定理,得MN2=OM2+ON2-2OM·ON·cos
即……………………4分
………………6分
当即快艇必须至少以80千米/小时速度行驶,
此时MN=……………………9分
设∠NMQ=……………………11分
故快艇的行驶方向为北偏东53°08′.…………………………12分
另解提示:在△OMN中,
∴当
22、解:(1)设, 对 由余弦定理, 得
,解出 ……………5分
(2)考虑直线的斜率的存在性,可分两种情况:
i) 当k存在时,设l的方程为………………① …………7分
椭圆方程为
由 得. …………8分
于是椭圆方程可转化为………………②
将①代入②,消去得,
整理为的一元二次方程,得.
则、是上述方程的两根.且,
EMBED Equation.3 ,
AB边上的高
………………9分
ii) 当k不存在时,把直线代入椭圆方程得
………………11分
由①②知S的最大值为 由题意得=12 所以
故当面积最大时椭圆的方程为: ………………14分
下面给出本题的另一解法,请读者比较二者的优劣:
设过左焦点的直线方程为:…………① …………………3分
(这样设直线方程的好处是什么?还请读者进一步反思反思.)
椭圆的方程为:
由得:于是椭圆方程可化为:……②
把①代入②并整理得: ………………5分
于是是上述方程的两根.
,……7分
AB边上的高,
从而
………………10分
当且仅当取等号,即
由题意知, 于是.
故当△面积最大时椭圆的方程为: …………………14分
A
B
C
D
A1
B1
C1
D1
10米
10米
4米
4米
也可这样求解:
PAGE
5
第I卷
一、选择题(本大题共12个小题,每小题5分,共60分)
1、的值为 ( )
A. B. C. D.
2、抛物线的焦点坐标是 ( )
A. B.(,0) C.(1,0) D.(0,1)
3、若,,则下列不等式成立的是
A. B. C. D.
4、数列,则a25等于 ( )
A.570 B.300 C.285 D.276
5、两点P(4,-9),Q(-2,3),y轴与直线PQ交于M且则为:( )
A. B. C.2 D. 3
6、已知△ABC的三内角A、B、C满足条件,则角A等于( )
A.30° B.60° C.70° D.120°
7、△ABC的三边长分别为AB=7,BC=5,CA=6,则的值为:………………( )
A.19 B.-19 C.-18 D.-14
8、若等于 ( )
A. B. C. D.
9、命题:“若,则”的逆否命题是( )
若,则;
若,则;
若,则;
若,则;
10、在等比数列 ( )
A.-2 B.-2或2 C. D.
11、已知,则的最小值是
A. B. C. D.25
12、点在椭圆=1上且到直线的距离为,那么点的个数为 ( )
A.1 ; B.2 ; C.3 ; D.4;
二、填空题:(本大题共4个小题,每小题4分,共16分)将答案填在答题纸指定位置
13、命题“”的否定是:
14、已知cos=,且,则cos( )= .
15、已知数列,则该数列的通项公式为 .
16、椭圆的焦点、,P为椭圆上的一点,已知,则△的面积为 .
三、解答题:(本大题共6小题,共74分,解答应写出必要的文字说明、证明过程或演算步骤)
17、(12分)已知.
(1)求的值;
(2)求的值.
18、(12分)已知等差数列
(1)求数列的通项公式;
(2)记数列的前n项和记为Sn,求Sn.
19、(12分)某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米。
(1)若设休闲区的长米,求公园ABCD所占面积S关于的函数的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
20、(12分)已知向量
⑴;
⑵若
21、(12分)如图所示,一辆汽车从O点出发,沿海岸线一直线公路以100千米/小时的速度向东匀速行驶.汽车开动时,在距O点500千米,且与海岸线距离400千米的海面上M点处有一艘快艇与汽车同时出发,要把一件重要物品送给这辆汽车司机.该快艇至少以多大的速度行驶,才能将物品送到司机手中?并求出此时快艇行驶的方向.
(参考数据:)
22、(14分)已知椭圆C的中心在原点,焦点、在x轴上,点P为椭圆上的一个动点,且 的最大值为90°,直线过左焦点与椭圆交于A、B两点,的面积最大值为12.
(1)求椭圆C的离心率;(5分)
(2)求椭圆C的方程。(9分)
高二教学过程检测数学试题参考答案(理科)
一、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D C B C A B C D D B B
二、填空题:
13. 14. 15. 16. 9
三、解答题:
17、解:(1)
……………………2分
…………………………5分
(2)
=…………………………7分
…………………………10分
=-1……………………12分
18、解:(1)由题意得……………………2分
解得……………………4分
……………………6分
(2)由(1)得
……………………8分
……………………10分
……………………12分
19、解:⑴由,知
⑵
当且仅当时取等号
∴要使公园所占面积最小,休闲区A1B1C1D1的长为100米、宽为40米.
20、解:⑴
⑵(理科)
①当时,当县仅当时,取得最小值-1,这与已知矛盾;
②当时,取得最小值,由已知得
;
③当时,取得最小值,由已知得
解得,这与相矛盾,综上所述,为所求.
21、解:如图所示,设快艇从M处以v千米/小时的速
度出发,沿MN方向航行,t小时后在N点与汽
车相遇,MQ为M点到ON的距离,则MQ=400,
在△MON中,MO=500,ON=100t,MN=vt
设∠MON=,由题意知
……………………2分
由余弦定理,得MN2=OM2+ON2-2OM·ON·cos
即……………………4分
………………6分
当即快艇必须至少以80千米/小时速度行驶,
此时MN=……………………9分
设∠NMQ=……………………11分
故快艇的行驶方向为北偏东53°08′.…………………………12分
另解提示:在△OMN中,
∴当
22、解:(1)设, 对 由余弦定理, 得
,解出 ……………5分
(2)考虑直线的斜率的存在性,可分两种情况:
i) 当k存在时,设l的方程为………………① …………7分
椭圆方程为
由 得. …………8分
于是椭圆方程可转化为………………②
将①代入②,消去得,
整理为的一元二次方程,得.
则、是上述方程的两根.且,
EMBED Equation.3 ,
AB边上的高
………………9分
ii) 当k不存在时,把直线代入椭圆方程得
………………11分
由①②知S的最大值为 由题意得=12 所以
故当面积最大时椭圆的方程为: ………………14分
下面给出本题的另一解法,请读者比较二者的优劣:
设过左焦点的直线方程为:…………① …………………3分
(这样设直线方程的好处是什么?还请读者进一步反思反思.)
椭圆的方程为:
由得:于是椭圆方程可化为:……②
把①代入②并整理得: ………………5分
于是是上述方程的两根.
,……7分
AB边上的高,
从而
………………10分
当且仅当取等号,即
由题意知, 于是.
故当△面积最大时椭圆的方程为: …………………14分
A
B
C
D
A1
B1
C1
D1
10米
10米
4米
4米
也可这样求解:
PAGE
5
