人教版数学五年级下册 第五单元 图形的旋转 例1例2 课件(34张ppt)
文档属性
| 名称 | 人教版数学五年级下册 第五单元 图形的旋转 例1例2 课件(34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 10:07:05 | ||
图片预览





文档简介
五年级下册 数学 第五单元
图形的运动(三)
—— 旋转
1. 通过生活事例,进一步感知旋转的现象,理解图形旋转的含义。
2.掌握图形旋转的三要素并会描述物体的旋转过程。
3. 能初步感知图形旋转的特征,发展空间想象能力。
学习目标
你还记得这些是什么现象吗?
1.生活中,你还见过哪些旋转现象?
2.下面物体的运动有什么共同点呢?
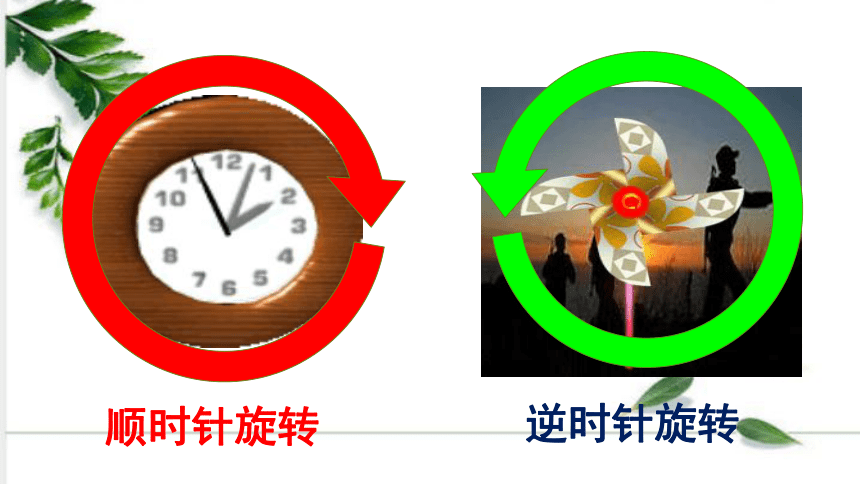
物体绕着一个点或一条轴运动的现象叫做旋转。
顺时针旋转
逆时针旋转
观察思考:
指针在钟表中旋转一周是( )度,12个时刻所在直线把圆等分成12份,每份是( )度。
360
30
360°÷12=30°
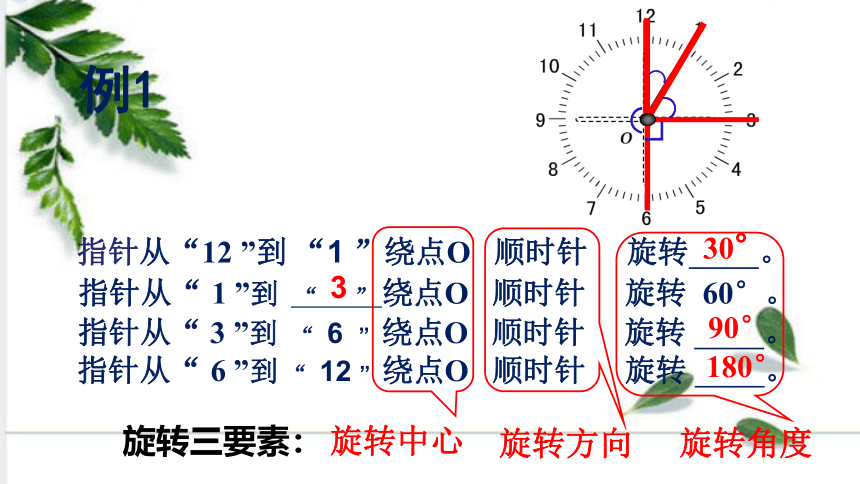
指针从“12 ”到 “1 ”绕点O 顺时针 旋转 。
指针从“ 1 ”到 “ ” 绕点O 顺时针 旋转 60°。
指针从“ 3 ”到 “ 6 ” 绕点O 顺时针 旋转 。
指针从“ 6 ”到 “ 12 ” 绕点O 顺时针 旋转 。
3
90°
180°
旋转中心
旋转方向
旋转角度
30°
旋转三要素:
⌒
∟
⌒
⌒
例1
01
02
03
旋转
三要素
旋转中心
旋转方向
旋转角度
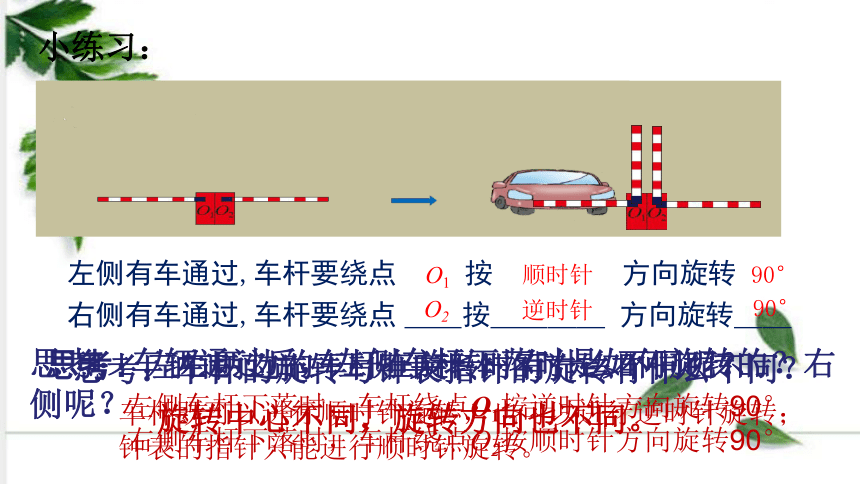
左侧有车通过,车杆要绕点 O1 按 顺时针 方向旋转 90°
右侧有车通过,车杆要绕点 __按____ 方向旋转__
逆时针
90°
O2
小练习:
思考:左右两边的车杆在旋转时有什么不同呢?
旋转中心不同,旋转方向也不同。
思考:车辆通过后,左侧车杆下落时是如何旋转的?右侧呢?
左侧车杆下落时,车杆绕点O1按逆时针方向旋转90°
右侧车杆下落时,车杆绕点O2按顺时针方向旋转90°
思考:车杆的旋转与钟表指针的旋转有什么不同?
车杆既可以进行顺时针旋转,也可以进行逆时针旋转;
钟表的指针只能进行顺时针旋转。
o
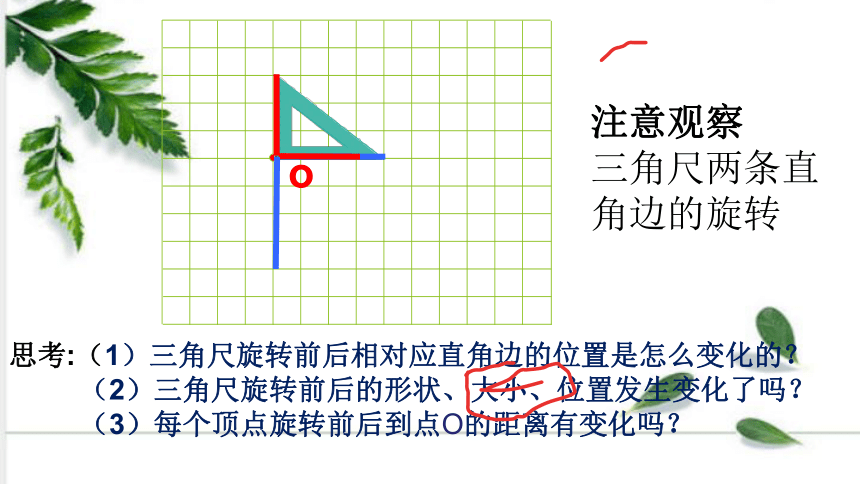
思考:(1)三角尺旋转前后相对应直角边的位置是怎么变化的?
(2)三角尺旋转前后的形状、大小、位置发生变化了吗?
(3)每个顶点旋转前后到点O的距离有变化吗?
注意观察
三角尺两条直角边的旋转
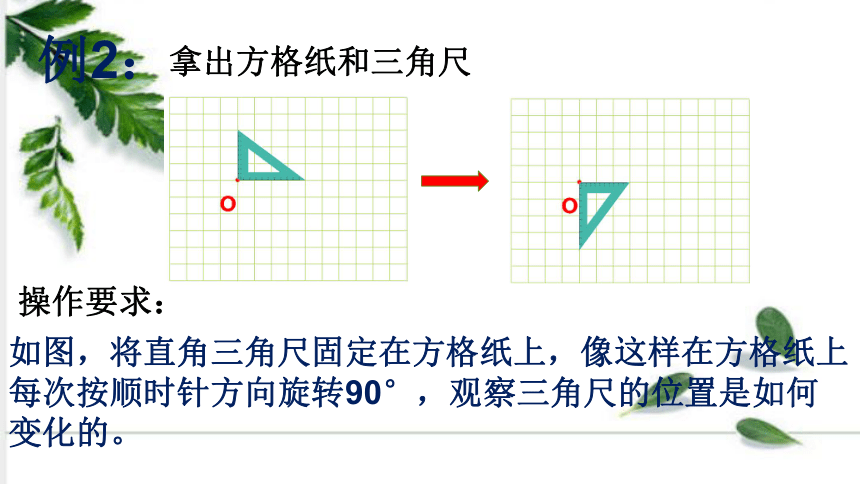
如图,将直角三角尺固定在方格纸上,像这样在方格纸上每次按顺时针方向旋转90°,观察三角尺的位置是如何变化的。
拿出方格纸和三角尺
例2:
操作要求:
旋 转
旋转 1
旋转 2
旋转 3
旋转 4
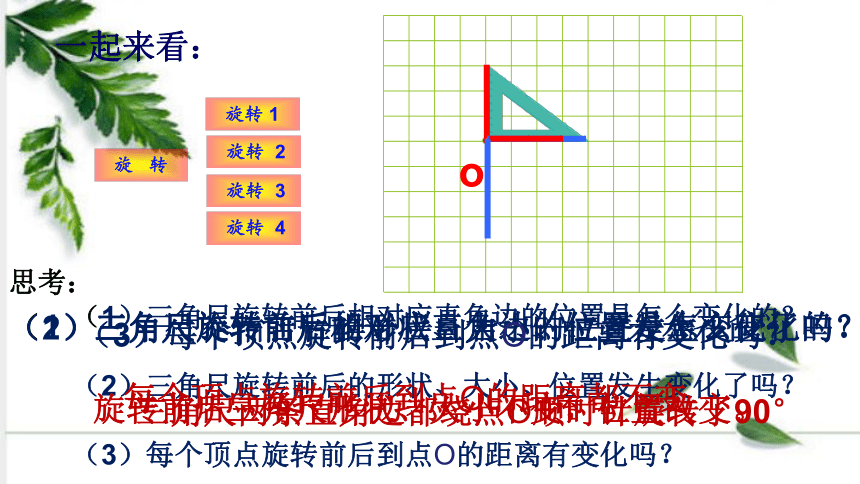
一起来看:
o
思考:
(1)三角尺旋转前后相对应直角边的位置是怎么变化的?
(2)三角尺旋转前后的形状、大小、位置发生变化了吗?
(3)每个顶点旋转前后到点O的距离有变化吗?
(1)三角尺旋转前后相对应直角边的位置是怎么变化的?
(2)三角尺旋转前后的形状、大小、位置发生变化了吗?
旋转前后三角尺形状、大小不变,位置改变。
三角尺两条直角边都绕点O顺时针旋转了90°
(3)每个顶点旋转前后到点O的距离有变化吗?
每个顶点旋转前后到点O的距离都不变
旋转中心的位置不变,三角形的每条边都绕点O旋转了90°,图形的形状、大小不变,只是图形的位置变了,每个顶点旋转前后到点O的距离没有变。
图形旋转前后:
旋转的特征:
1.旋转前后旋转中心的位置不变,图形的形状和大小也不变,只是图形的位置变了。
2.过旋转中心的所有边旋转方向相同,旋转角度也相同。
3.每个顶点旋转前后到旋转中心的距离都不变。
小练习:
换另一把三角尺,在方格纸上按逆时针方向像上面那样转一转并说一说。
B
A
D
2.我会填
图形①是以点( )为中心旋转的。
图形②是以点( )为中心旋转的。
图形③是以点( )为中心旋转的。
90
9
120
从“ 12 ”到“ 3 ”,指针绕点O按顺时针方向旋转了( )°。
从“ 3 ”到“( )”,指针绕点O按顺时针方向旋转了180°。
( 2)
从“ 6 ”到“ 10 ”,指针绕点O按顺时针方向旋转了( ) °。
钟摆绕 点 O( )时针
旋转不超过 10°。
钟摆绕 点 O( )时针
旋转不超过 10°。
顺
逆
(3)
(1)下面的图形中,可通过旋转得到的是( )。
A. B. C. D.
D
3.我会选
(2)下面的游戏中,( )是旋转现象。
A.踢毽子 B.玩碰碰车
C.荡秋千 D.捉迷藏
C
(3)下列现象中,既有平移现象,又有旋转现象的是( )。
A.正在工作的风扇叶片 B.在笔直道路上行驶的汽车
C.运行中的观光电梯 D.传输带上的物品
B
(4)从3时15分到3时45分这段时间里,钟表上的分针旋转了( )。
120° B. 180°
C. 30° D. 360°
B
———
分针指向3
————
分针指向9
30°×6=180°
分针走了6个大格
4.
旋转的风车
风车绕点O逆时针旋转了( )度。
O
90
风车绕点O逆时针旋转了( )度。
O
180
(四)美图欣赏
今天你有哪些收获?
再
见
图形的运动(三)
—— 旋转
1. 通过生活事例,进一步感知旋转的现象,理解图形旋转的含义。
2.掌握图形旋转的三要素并会描述物体的旋转过程。
3. 能初步感知图形旋转的特征,发展空间想象能力。
学习目标
你还记得这些是什么现象吗?
1.生活中,你还见过哪些旋转现象?
2.下面物体的运动有什么共同点呢?
物体绕着一个点或一条轴运动的现象叫做旋转。
顺时针旋转
逆时针旋转
观察思考:
指针在钟表中旋转一周是( )度,12个时刻所在直线把圆等分成12份,每份是( )度。
360
30
360°÷12=30°
指针从“12 ”到 “1 ”绕点O 顺时针 旋转 。
指针从“ 1 ”到 “ ” 绕点O 顺时针 旋转 60°。
指针从“ 3 ”到 “ 6 ” 绕点O 顺时针 旋转 。
指针从“ 6 ”到 “ 12 ” 绕点O 顺时针 旋转 。
3
90°
180°
旋转中心
旋转方向
旋转角度
30°
旋转三要素:
⌒
∟
⌒
⌒
例1
01
02
03
旋转
三要素
旋转中心
旋转方向
旋转角度
左侧有车通过,车杆要绕点 O1 按 顺时针 方向旋转 90°
右侧有车通过,车杆要绕点 __按____ 方向旋转__
逆时针
90°
O2
小练习:
思考:左右两边的车杆在旋转时有什么不同呢?
旋转中心不同,旋转方向也不同。
思考:车辆通过后,左侧车杆下落时是如何旋转的?右侧呢?
左侧车杆下落时,车杆绕点O1按逆时针方向旋转90°
右侧车杆下落时,车杆绕点O2按顺时针方向旋转90°
思考:车杆的旋转与钟表指针的旋转有什么不同?
车杆既可以进行顺时针旋转,也可以进行逆时针旋转;
钟表的指针只能进行顺时针旋转。
o
思考:(1)三角尺旋转前后相对应直角边的位置是怎么变化的?
(2)三角尺旋转前后的形状、大小、位置发生变化了吗?
(3)每个顶点旋转前后到点O的距离有变化吗?
注意观察
三角尺两条直角边的旋转
如图,将直角三角尺固定在方格纸上,像这样在方格纸上每次按顺时针方向旋转90°,观察三角尺的位置是如何变化的。
拿出方格纸和三角尺
例2:
操作要求:
旋 转
旋转 1
旋转 2
旋转 3
旋转 4
一起来看:
o
思考:
(1)三角尺旋转前后相对应直角边的位置是怎么变化的?
(2)三角尺旋转前后的形状、大小、位置发生变化了吗?
(3)每个顶点旋转前后到点O的距离有变化吗?
(1)三角尺旋转前后相对应直角边的位置是怎么变化的?
(2)三角尺旋转前后的形状、大小、位置发生变化了吗?
旋转前后三角尺形状、大小不变,位置改变。
三角尺两条直角边都绕点O顺时针旋转了90°
(3)每个顶点旋转前后到点O的距离有变化吗?
每个顶点旋转前后到点O的距离都不变
旋转中心的位置不变,三角形的每条边都绕点O旋转了90°,图形的形状、大小不变,只是图形的位置变了,每个顶点旋转前后到点O的距离没有变。
图形旋转前后:
旋转的特征:
1.旋转前后旋转中心的位置不变,图形的形状和大小也不变,只是图形的位置变了。
2.过旋转中心的所有边旋转方向相同,旋转角度也相同。
3.每个顶点旋转前后到旋转中心的距离都不变。
小练习:
换另一把三角尺,在方格纸上按逆时针方向像上面那样转一转并说一说。
B
A
D
2.我会填
图形①是以点( )为中心旋转的。
图形②是以点( )为中心旋转的。
图形③是以点( )为中心旋转的。
90
9
120
从“ 12 ”到“ 3 ”,指针绕点O按顺时针方向旋转了( )°。
从“ 3 ”到“( )”,指针绕点O按顺时针方向旋转了180°。
( 2)
从“ 6 ”到“ 10 ”,指针绕点O按顺时针方向旋转了( ) °。
钟摆绕 点 O( )时针
旋转不超过 10°。
钟摆绕 点 O( )时针
旋转不超过 10°。
顺
逆
(3)
(1)下面的图形中,可通过旋转得到的是( )。
A. B. C. D.
D
3.我会选
(2)下面的游戏中,( )是旋转现象。
A.踢毽子 B.玩碰碰车
C.荡秋千 D.捉迷藏
C
(3)下列现象中,既有平移现象,又有旋转现象的是( )。
A.正在工作的风扇叶片 B.在笔直道路上行驶的汽车
C.运行中的观光电梯 D.传输带上的物品
B
(4)从3时15分到3时45分这段时间里,钟表上的分针旋转了( )。
120° B. 180°
C. 30° D. 360°
B
———
分针指向3
————
分针指向9
30°×6=180°
分针走了6个大格
4.
旋转的风车
风车绕点O逆时针旋转了( )度。
O
90
风车绕点O逆时针旋转了( )度。
O
180
(四)美图欣赏
今天你有哪些收获?
再
见
